Auch wenn ich es letzte Woche schon erklärt habe – so ganz leicht ist es ja nicht zu verstehen, wie so eine Raumverzerrung eigentlich funktioniert, wenn eine Gravitationswelle (kurz GW) sich durchs All ausbreitet oder auf einen Detektor wie LIGO trifft. Was ändert sich bei so einer Raumverzerrung? Wie können wir sie messen? Die Kommentare zum letzten Text zeigen, dass das schon etwas knifflig ist, deswegen versuche ich es heute nochmal etwas anders (auch wenn die Argumente im Kern dieselben sind.)
Ein Problem bei den Überlegungen ist vermutlich, dass die Bilder, die man zur Veranschaulichung gern zeigt, etwas irreführend sind. Nehmen wir (wie so oft) diese schöne Animation einer GW von Markus Pössel :
Auf dem Bild sieht es so aus, als würde der rote Punkt in der Mitte in Ruhe bleiben, und Punkte bewegen sich um so stärker, je weiter sie von diesem Mittelpunkt entfernt sind. Das ist aber nur ein Problem der Darstellung. Ein ähnliches Problem gibt es z.B. auch bei Darstellungen der Expansion des Weltalls wie dieser hier:

By Leipnizkeks, CC BY-SA 3.0, Link
Auch hier sieht es so aus, als würde ein Punkt in der Mitte sich nicht bewegen, ein Punkt am Rand besonders stark.
In beiden Fällen liegt das aber nur an der Veranschaulichung – in Wahrheit sind alle Punkte gleichberechtigt. (Warnhinweis: Bei der GW gilt das für alle Punkte in einer Ebene senkrecht zur Ausbreitungsrichtung einer unendlich großen Welle – das sehen wir gleich noch.)
Das Messgitter
Damit wir ganz genau sehen können, wie eine GW wirkt, suchen wir uns ein ungestörtes Plätzchen. Irgendwo im Weltall, fernab von aller störenden Materie, oder überhaupt allem. Meinetwegen irgendwo zwischen Andromeda-Nebel und unserer Galaxis (wir können uns ja bei den Maahks die Midway-Station ausleihen). In diesem ruhigen Plätzchen machen wir es uns gemütlich. Um sicher zu sein, dass auch wir wirklich ruhig sind, können wir zum Beispiel die Hintergrundstrahlung verwenden und unsere Geschwindigkeit solange anpassen, bis die völlig isotrop ist, das ist so ziemlich die beste Annäherung an “in Ruhe sein”, die es gibt.
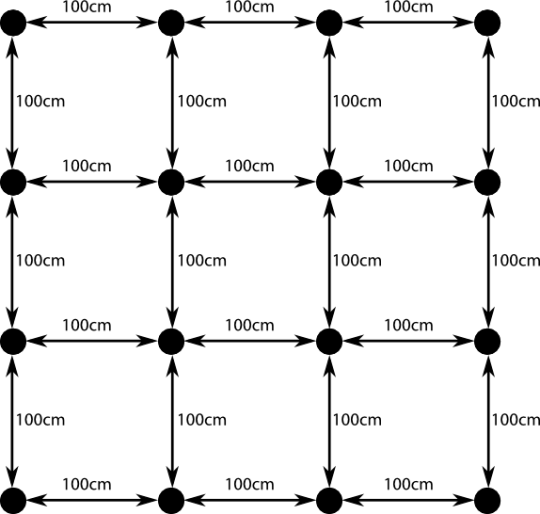
Jetzt bauen wir eine Messapparatur auf. Die besteht aus lauter kleinen Kugeln (die wir uns so leicht denken können, dass sie sich gegenseitig nicht nennenswert anziehen). Wir ordnen diese Kugeln in einem Gittermuster an, so dass jede Kugel von ihrer Nachbarkugel genau einen Meter entfernt ist:
Das können wir mit einem Maßband feststellen, das wir in der Tasche haben oder wir befestigen auf den Kugeln Laser und Spiegel und messen die Lichtlaufzeit zwischen den Kugeln. Wichtig ist, dass die Kugeln vollkommen frei sind und dass auf sie keine Kräfte wirken. (Letztlich ist das dieselbe Idee, die ich seinerzeit als “Raumzeitstaub” bezeichnet habe.) Die Kugeln verfügen auch – erst mal – über keinen Mechanismus, der ihren Abstand irgendwie konstant halten soll oder sonst etwas.
Solange nichts weiter passiert (Dinge wie die Expansion des Alls ignorieren wir mal), bleibt der Abstand unserer Kugeln beim Wert 1 Meter. Ihr könnt leicht nachrechnen, dass auf diesem schönen Gitter alle Regeln der Euklidischen Geometrie gelten, unser Raum hat also keine Krümmung, die Welt ist einfach und auch Newton wäre mit diesem Bild sehr einverstanden.
Die Welle trifft aufs Gitter
Jetzt soll eine GW auf unser Gitter treffen, und zwar genau von oben. Normal sind solche Wellen einigermaßen kugelsymmetrisch, aber wenn man weit genug vom Ursprung der Welle weg ist, dann verläuft die Wellenfront praktisch vollkommen gerade:
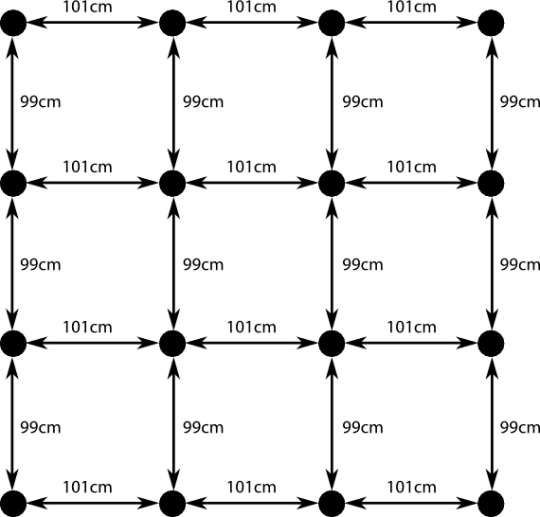
Wir stellen uns vor, dass eine solche Wellenfront genau senkrecht auf unser Gitter trifft. Statt jetzt Bildchen wie die Animation oben zu malen, können wir die Wirkung der Welle direkt dadurch veranschaulichen, dass wir uns anschauen, was sie mit dem Abstand zwischen den Kugeln macht. Nehmen wir an, die Dehnungsamplitude der GW ist 1% – das ist für eine GW unglaublich viel (und würde vermutlich dazu führen, dass es leichte Abweichungen im Verhalten der GW gibt, weil sich die Raumkrümmungen der Welle beeinflussen würden, aber das ignoriere ich auch, ich nehme den Wert nur, damit die Sache anschaulich ist – konzeptionell macht es keinen Unterschied, wenn man mit realistischen Dehnungswerten von 10^-21 oder so arbeitet). Ich nehme auch an, dass die Frequenz der Welle sehr niedrig ist, so niedrig, dass ich sehr viel zeit habe, um alles nachzumessen.
Ich rolle also wieder mein Maßband aus und messe den Abstand zwischen den Kugeln. Das Messergebnis sieht so aus:
Ihr seht, dass die Abstände sich in der einen Richtung verkürzt, in der anderen verlängert haben. (Expertinnenhinweis: Ich habe eine linear (Hier stand “longitudinal”, was Quatsch ist, danke HerrSenf) polarisierte GW angenommen.) Der Abstand der Kugeln hat sich also geändert. Ihr seht, dass diese Art der Darstellung den großen Vorteil hat, dass man sofort sieht, dass alle Punkte sich gleich verhalten. (Theoretisch ist die Welle natürlich nicht unendlich groß und am Rand wird ihr Effekt dann abgeschwächt sein, aber wir nehmen ja eine sehr ausgedehnte Welle an, siehe oben.)
Dass die Welle den Raum verzerrt, bedeutet genau, dass sich die messbaren Abstände zwischen den Kugeln ändern. Man darf nicht den Fehler machen zu glauben, dass sich auch die Länge unseres Maßbandes mit ändert, wenn ich es ausrolle (ich habe extra ein zum Aufrollen genommen, damit es (nahezu) unbeeinflusst bleibt, solange es aufgerollt in meiner Tasche ist). Man ist oft versucht zu glauben: Aha, es ist jetzt “weniger Raum da”, also muss das Maßband sich zusammenquetschen – so wie man vielleicht ein Kissen in einen etwas zu engen Kissenbezug reinstopft. Aber so ist es nicht.
Auch Licht, das ich zwischen den Kugeln hin- und herschicke, ändert seine Laufzeit entsprechend – es verkürzt nicht etwa seine Wellenlänge, um doch noch reinzupassen. (Wäre es nicht so, würde sich also alle Materie und das Licht und alles genau an den “engeren Raum” anpassen, dann könnten wir von einer Raumkrümmung nie etwas merken – dann wäre das Konzept unnötig.)
Dass sich den Raum verzerrt, bedeutet eben, dass sich der Abstand zwischen unseren Kugeln ändert. Dieser geänderte Abstand ist messbar – wie wir ihn messen, ist dabei erstmal egal, solange das Messverfahren vernünftig geeicht ist. (Mehr über GW findet ihr übrigens auch in diesem Text.)
Hinweis: Wenn man diese Art der Darstellung nutzt, dann ist es sinnvoll, wirklich nur die Zahlen an den Linien im Gitter zu ändern, aber die Punkte nicht zu verschieben. Auch eine Dehnung um zum Beispiel 50% in einer Richtung würde ich immer noch so darstellen wie oben – das Gitter, das ich zeichne, würde ich nicht verzerrt zeichnen. Die Position der Kugeln in meiner Zeichnung ist letztlich willkürlich – in der Sprache der Allgemeine Relativitätstheorie (ART) ist das ein globales Koordinatensystem. Jeder Kugel ist ein Punkt auf meinem Blatt zugeordnet, aber es ist nicht notwendig, dass die genaue Position der Puntke auf dem Blatt mit der in der Realität übereinstimmt. Das Koordinatensystem ist dabei vollkommen willkürlich – man kann es so wählen, wie es für den jeweiligen Zweck angemessen ist. Das ist genau wie zum Beispiel bei einer Landkarte – viele Stadtpläne (also diese altertümlichen gedruckten Dinger) verwenden ja zum Beispiel eine Darstellung, bei der der Maßstab in einem Stadtzentrum kleiner ist und sich nach außen hin vergrößert, so dass man die engen Straßen im Zentrum besser erkennen kann.








Kommentare (55)