“Spannung” ist einer dieser etwas überfrachteten Begriffe – schon in der Physik können wir damit zwei ganz verschiedene Dinge meinen, nämlich die elektrische Spannung (z.B. die 9V von einer Blockbatterie) oder die mechanische Spannung. (Vom Alltagsbegriff rede ich hier gar nicht und ich rege mich jetzt auch nicht darüber auf, dass man aktuell in der Wissenschaftskommunkation jedes Forschungsergebnis, zu dem einen nicht einfällt, wie man es interessant darstellen soll, als “spannend” bezeichnet (ja, habe ich in der Vergangenheit auch mal gemacht, macht es nicht besser…). Nein, darüber rege ich mich nicht auf, obwohl ich es total nervig und abgegriffen finde und … [atmet tief durch, zählt bis 10]).
Wo war ich? Ach ja, die Spannung in der Physik. Wie gesagt, auch da schon ein etwas überfrachteter Begriff, aber meist nicht so schlimm, weil man aus dem Zusammenhang weiß, ob es um die elektrische oder mechanische Spannung geht. (Es sei denn, man redet über Piezomaterialien, wo eine angelegte elektrische Spannung eine mechanische Spannung verursacht, dann muss man aufpassen, das erlebe ich jedes Jahr wieder in meiner Funktionswerkstoffe-Vorlesung.)
Hier und heute reden wir aber nur über die mechanische Spannung, ein von Studis im Maschinenbau eher nicht so geschätztes, aber doch spannendes (aargh!) wichtiges Thema.
Wir fangen mit einem kleinen Experiment an: Nehmt euch ein Gummiband (oder stellt es euch vor) und zieht es ein wenig in die Länge. Ihr spürt jetzt, dass ihr mit euren Fingern eine Kraft auf das Gummiband ausüben müsst, um es langgezogen zu lassen; sobald ihr es loslasst, schnellt es (autsch) in seine Ausgangslänge zurück. (Dass es das tut, verdankt es übrigens der Entropie der aufgeknäulten Gummimoleküle.)

Wir brauchen also eine Kraft, um das Gummiband zu dehnen. Da kommt schon die erste Verständnishürde ins Spiel: Laut Definition der Kraft, die ihr bestimmt mal in der Schule unter dem Namen “zweites Newtonsches Gesetz” lernen musstet, ist Kraft gleich Masse mal Beschleunigung. Hier wird aber ja (wenn das Gummi erst mal gedehnt ist) gar nichts beschleunigt, also sollte es auch keine Kraft geben. (Etwas ausführlicher habe ich das in diesem Artikel erklärt, da habe ich auch angekündigt, eventuell mal was über den Begriff der Spannung zu schreiben, hat ja nicht mal 5 Jahre gedauert, bis ich das Versprechen wahr gemacht habe…)
Aber wenn an jedem Punkt die Kraft Null ist, warum ist dann das Gummiband gedehnt? Und warum schnappen die beiden Enden zurück, wenn ich es in der Mitte durchschneide?
Tatsächlich ist die Angelegenheit etwas komplizierter: Jeder Punkt im Gummi erfährt zwei Kräfte, eine nach links, eine nach rechts. Jede davon würde den Punkt beschleunigen, aber die Gegenkraft von der anderen Seite verhindert das. Wenn ich das Gummi durchschneide, dann fällt die Kraft von der einen Seite weg und das Gummi kann zurückschnappen. In der Summe sind diese beiden Kräfte Null, deswegen ist das Gummiband in Ruhe, aber zwei entgegengesetzte Kräfte, die beide Null sind, sind nicht dasselbe wie keine Kraft.
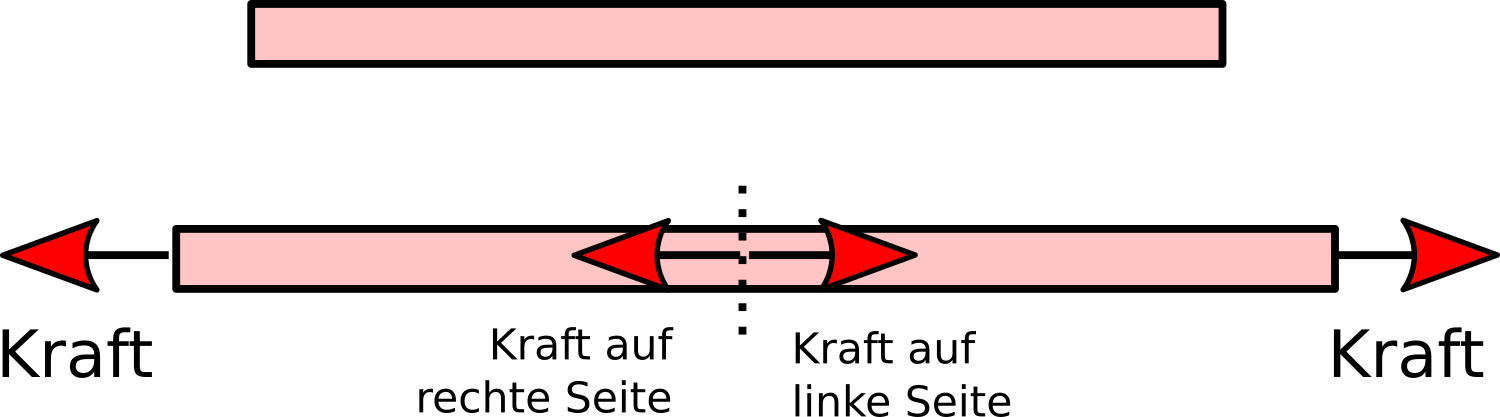
Schauen wir noch etwas genauer hin, dann sehen wir, dass hier zusätzlich das dritte Newtonsche Gesetz ins Spiel kommt: Kraft gleich Gegenkraft. Ausführlicher: Wenn ein Körper eine Kraft auf einen zweiten ausübt, dann übt der zweite Körper auch eine Kraft auf den ersten aus, die genau entgegengesetzt ist. Wir können das Gummiband gedanklich in zwei Teile teilen – der linke Teil übt eine Kraft auf den rechten aus und umgekehrt, beide sind entgegengesetzt, in der Summe ergibt sich an jedem Punkt Null. (Es ist ein nettes Gedankenexperiment, sich vorzustellen, das 3. Newton-Gesetz würde nicht gelten. Das mache ich hier nicht, habe ich aber in meinem Buch zur Relativitätstheorie getan.)
Der Begriff der Spannung
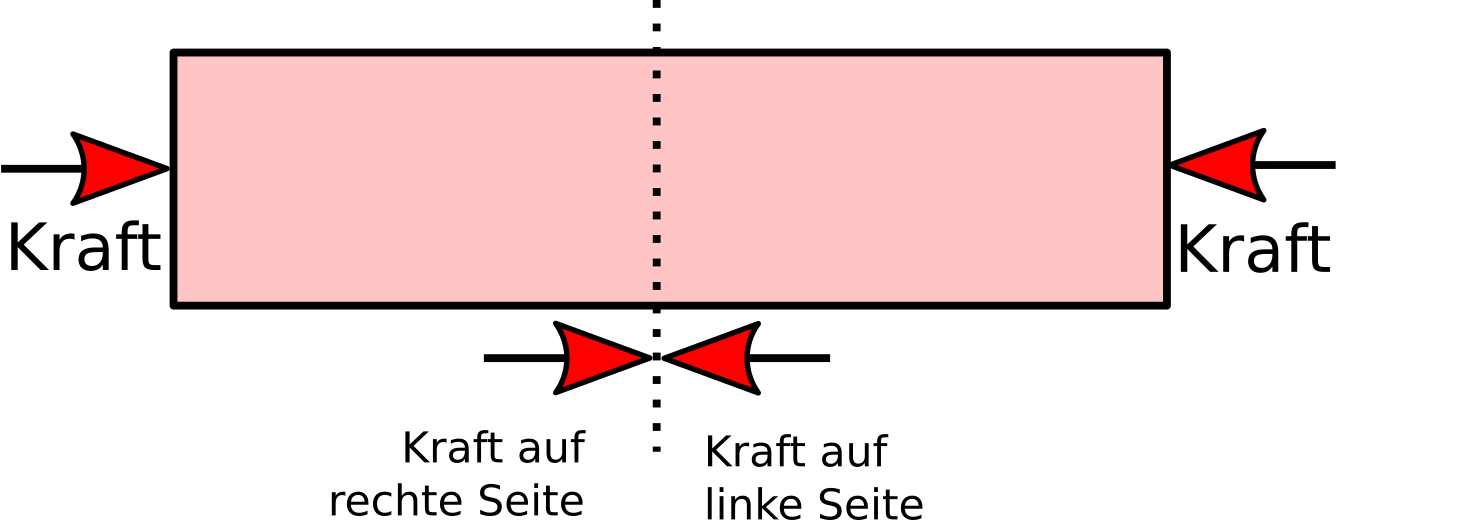
Bisher habe ich nur von Kräften geredet, nicht von Spannungen. Warum der Begriff der Spannung sinnvoll ist, seht ihr, wenn ihr das Gummiband gedanklich wieder in zwei Teile teilt, diesmal aber der Länge nach. Um jede einzelne der beiden Hälften zu dehnen, braucht ihr logischerweise die halbe Kraft. Wenn ihr euch fragt, was im Material passiert, dann ist es einem kleinen Stück Gummi egal, ob es zu einem Band mit voller oder mit halber Breite gehört, lokal an diesem Punkt passiert genau dasselbe.

Deswegen ist es sinnvoll, die Kraft auf die Fläche zu beziehen, und genau das nennt man die Spannung. Die Spannung ist also definiert als Kraft pro Fläche. Wenn ich eine Kraft von einem Newton brauche, um das Gummi um einen Zentimeter in die Länge zu ziehen, dann brauche ich nur ein halbes Newton für ein halb so breites Gummiband und zwei Newton für ein doppelt so breites. In jedem Fall passiert im Material dasselbe, es ist nur mal mehr, mal weniger Material da. (Das ist auch praktisch wichtig: Wenn ihr einen Kran aus Stahl bauen wollt, wollt ihr die Materialeigenschaften nicht an meterlangen Stahlproben oder ganzen Kränen messen, sondern an kleinen, handhabbaren Proben. Sonst geht es euch wie dem Vater bei Calvin und Hobbes…)
(Kleine Nebenbemerkung: genauso wie es sinnvoll ist, die Kraft auf die Fläche zu beziehen, ist es auch sinnvoll, die Längenänderung auf die Länge zu beziehen. Wenn ihr mit einer Kraft von 1 Newton ein 10cm langes Gummiband um 1cm in die Länge ziehen könnt, dann könnt ihr mit derselben Kraft ein 20cm langes Gummiband um 2cm in die Länge ziehen. Das muss so sein, wenn ihr wieder mit Kraft=Gegenkraft argumentiert. Teilt das Gummi gedanklich der Länge nach in zwei Hälfte, am linken Ende des linken und am rechten Ende des rechten Gummis wirkt die Kraft 1N, also wirkt diese Kraft auch in der Mitte von jeweils einer Hälfte auf die andere. In der Mechanik guckt man deswegen auf die Dehnung, das ist die Längenänderung bezogen auf die Länge, hier ist sie also 10%. Und damit wisst ihr jetzt auch, warum wir MaterialwissenschaftlerInnen uns dauernd mit so genannten Spannungs-Dehnungs-Kurven herumschlagen müssen…)
Zurück zur Spannung. Die ist also definiert als Kraft pro Fläche. Kräfte haben eine Richtung (ich ziehe ja am Gummi auf der einen Seite nach links, auf der anderen nach rechts), also sollte auch die Spannung eine Richtung haben. Fragt sich nur, welche. Wenn ihr wieder die Mitte unseres Gummibands betrachtet, seht ihr, dass das nicht so offensichtlich ist: Hier wirkt ja eine Kraft von rechts, die das Gummi nach rechts ziehen will, und eine von links, die das Gummi nach links ziehen will. Zeigt die Spannung nun nach links oder nach rechts?
Die Antwort auf diese Frage lautet: “Ja”. Oder auch “nein”, ganz wie ihr wollt. Bevor ihr jetzt denkt, dass mir der aktuell herrschende Dauerregen aufs Hirn geschlagen ist, keine Sorge. Ist er nicht. (Glaube ich jedenfalls. Wobei ich mich natürlich fragen muss, ob ich es merken würde, wenn es anders wäre…)
Was ich gerade zu erklären versuche ist, dass die Richtungsabhängigkeit der Spannung etwas komplizierter ist als die einer Kraft. Wenn wir an beiden Enden des Gummibands ziehen, dann ist der Spannungszustand im Gummi eben so, dass an jedem Punkt des Gummis zwei Kräfte wirken, die diesen Punkt jeweils nach außen hin ziehen wollen. Deshalb nennen wir so etwas eine Zugspannung.
Man kann sich das auch so veranschaulichen, dass man sich fragt: Wenn ich das Gummiband zerschneiden würde, aber trotzdem dafür sorgen möchte, dass es seine Form dabei nicht ändert, welche Kräfte bräuchte ich dafür? Dann seht ihr, dass ihr auf die Schnittfläche der linken Seite eine Kraft nach rechts ausüben müsst, auf die Schnittfläche der rechten Seite eine Kraft nach links. So erklären es übrigens auch die meisten Bücher zur Mechanik.
Umgekehrt gibt es auch Druckspannungen. Die kann man mit einem Gummiband nicht so gut zeigen, aber mit einem Gummiklotz (z.B. einem weichen Radiergummi) schon: Nehmt das Radiergummi zwischen zwei Finger und drückt zusammen. Wenn ihr jetzt eine Ebene in der Mitte des Gummis betrachtet, wirken wieder zwei Kräfte, eine von links, eine von rechts, die sich gegenseitig aufheben. Diesmal wirken die beiden Kräfte aber jeweils in die andere Richtung, von links kommt eine Kraft, die nach rechts wirkt, von rechts kommt eine Kraft, die nach links wirkt.
Die Spannung hat also eine komplizierte Richtungsabhängigkeit. Wie kompliziert die werden kann, sehen wir gleich noch etwas genauer, aber ihr könnt schon an diesem einfachen Beispiel, wo wir nur ziehen oder drücken, sehen, dass die Spannung etwas anderes ist als eine Kraft, denn eine Kraft hat immer eine einzige, klar definierte Richtung. (Mathematisch ist die Kraft damit ein Vektor.) Interessanterweise wird diese Subtilität in keinem Buch zur Mechanik so erklärt, wie ich es hier tue, und zumindest mich hat die Frage “Warum genau ist eigentlich eine Zug- oder Druckspannung in einer Richtung nicht einfach eine Kraft, obwohl sie als Kraft pro Fläche definiert ist?” am Anfang immer etwas verwirrt.
Noch mehr Richtungen
Ich hoffe, ihr seid noch nicht zu verwirrt, denn es wird noch etwas komplizierter. Nehmt wieder das Radiergummi zur Hand, aber statt draufzudrücken, schert ihr es jetzt ab: Haltet es an der Unterseite fest und verschiebt jetzt die Oberseite parallel zur Unterseite nach rechts. Wenn ihr wollt, könnt ihr vorher ein senkrechtes Kreuz auf das Gummiband malen, dann seht ihr, dass die Linien des Kreuzes jetzt nicht länger oder kürzer werden, sie ändern aber ihren Winkel zueinander. So etwas nennt man eine Scherung, die zugehörige Spannung heißt Scher- oder Schubspannung.
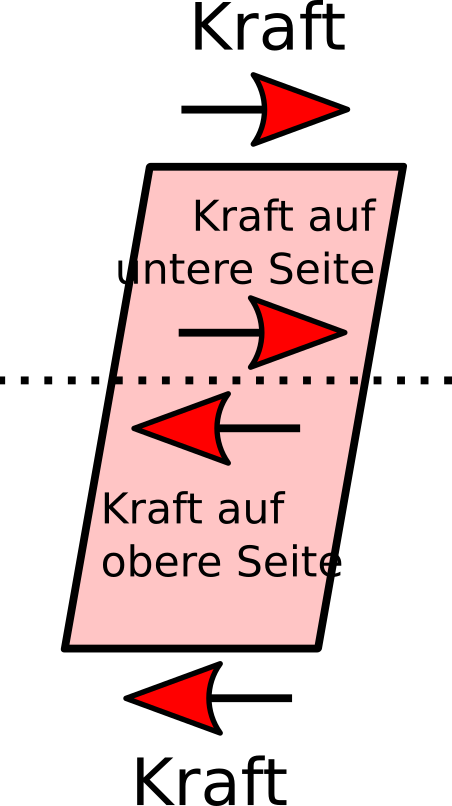
Was passiert hier? Denkt euch wieder eine Ebene in der Mitte des Gummis, entlang derer ihr das Gummi zerschneidet. Jetzt würde die untere Seite des Gummis sich nach links bewegen, die obere nach rechts. Wir haben jetzt also eine Kraft, die parallel zu der gedachten Schnittfläche wirkt, nicht senkrecht dazu wie vorher bei der Zug- oder Druckspannung. (Nebenbemerkung: Man kann so eine Schubverformung allerdings auf eine reine Dehnung und Stauchung zurückführen: Denkt euch ein kleines Quadrat, das ihr abschert, so dass daraus eine Raute wird. Ihr könnt dieselbe Verformung dadurch bekommen, dass ihr das Quadrat entlang der einen Diagonalen in die Länge zieht, entlang der anderen staucht. (Mathematisch nennt man das eine Hauptachsentransformation.) Hmm, heute bin ich Klammerkönig…)
Schauen wir noch einmal zurück auf unsere Zug- (oder Druck-) Spannung. Da haben wir die Schnittebene quer zum Gummiband (oder Gummiklotz) gelegt, senkrecht zur Richtung der Kraft. Wir hätten sie allerdings auch parallel zum Gummiband legen können, so dass wir das Band gedanklich der Länge nach in zwei Teile teilen, so wie wir es gemacht haben, als wir uns überlegt haben, dass die Spannung als Kraft pro Fläche definiert werden sollte. Wenn wir das Band tatsächlich so zerschneiden, passiert schlicht gar nichts, denn auf diese Ebene wirkt ja keine Kraft.
Findet ihr das verwirrend? Es wirkt doch immer noch die Kraft längs des Gummibands. Das ist richtig, aber diese Kraft wirkt auf beiden Seiten der Schnittebene genau in gleicher Weise, es gibt also keinen Grund, warum irgendetwas passieren sollte, wenn man das Gummiband in dieser Richtung zerschneidet. Zerschneide ich das Band so, muss ich auf die Schnittfläche eben keine Kraft aufbringen, damit es seine aktuelle Form beibehält.
Dasselbe gilt für den abgescherten Gummiklotz: Wenn ihr ihn in senkrechter Richtung in zwei Teile teilt, passiert ebenfalls nichts, ihr habt jetzt einfach zwei abgescherte Gummiklötze.
[Noch ein Hinweis für die ganz Genauen: Wenn ihr jetzt sagt “Moment, die Schnittebene müsste doch unter einem schrägen Winkel liegen, weil ich das Material ja abschere”, dann habt ihr streng genommen natürlich vollkommen recht. Das müsste man tun, es macht die Sache aber (zumindest für beliebige Spannungszustände) sehr viel komplizierter, plötzlich müsst ihr euch mit so Größen wie Deformationsgradienten herumschlagen, müsst euch fragen, ob ihr lieber die Kirchhoff-, die Cauchy- oder doch die Mandelstahm-Spannung nehmen müsst und amüsiert euch mit Differentialgeometrie in gekrümmten Räumen. Kann man machen (und wenn man Spannungsberechnungen für Bauteile macht, tut man das auch, kann sich aber normalerweise drauf verlassen, dass die Leute, die die jeweilige Software programmiert haben, das richtig gemacht haben), aber das ist dann wirklich etwas jenseits dessen, was hier auf dem Blog geht. (Und so wahnsinnig gut kenne ich mich da auch nicht aus…) Ich nehme hier einfach mal an, dass die Abscherungen und Verformungen alle so klein sind, dass diese Unterschiede keine Rolle spielen.]
Damit sehen wir noch einmal ganz klar, dass die Spannung eine komplizierte Richtungsabhängigkeit hat: Sie hängt ab von der Richtung, in der wir unser Bauteil gedanklich zerschneiden, und von der Richtung der Kraft, die dann auf diese Ebene wirkt. Mathematisch ist so etwas ein Tensor. Um die Spannung vollständig zu beschreiben, reicht deshalb eine Zahl nicht, ihr braucht (in drei Dimensionen) sechs Zahlen. (Es sei denn, ihr habt es mit einem Cosserat-Kontinuum zu tun, dann braucht ihr neun.)
Ihr könnt diese komplizierte Richtungsabhängigkeit auch daran sehen, dass wir unseren Gummiklotz ja gleichzeitig in einer Richtung zusammendrücken und in einer anderen Richtung dran ziehen können. (Das hatte ich oben bei der Abscherung ja schon erwähnt.) Damit haben wir dann an einem Punkt also eine Druchspannung in einer Richtung und eine Zugspannung in einer anderen Richtung.
Spannungsfelder
Falls euch das alles noch nicht kompliziert genug war, hier noch eine weitere wichtige Komplikation: Die Spannung muss nicht überall dieselbe sein. In unserem Gummiband oder -klotz war sie das, weil wir sie in einfacher Weise verformt haben und weil sie auch eine einfache Form hatten. Dass es nicht immer so einfach sein muss, seht ihr, wenn ihr euch vorstellt, dass euer Gummiband an einer Stelle etwas schmaler ist. Dann habt ihr ihr weniger Querschnittsfläche, die Spannung (Kraft pro Fläche) muss hier also zunehmen. Weit weg von der Verengung im Gummiband ist die Spannung überall dieselbe und alle Kräfte wirken parallel zum Band. Aber wenn ihr der Verengung näherkommt, dann muss die Kraft umgeleitet werden. Die Spannung ist dann höher und zusätzlich wird auch der Spannungszustand komplizierter, weil nicht mehr alle Kraftlinien parallel zum Band liegen.
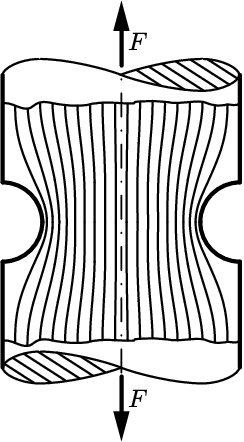
Bild aus Rösler, Harders, Bäker, “Mechanisches Verhalten der Werkstoffe”, Springer Verlag
In der Realität ist es so, dass die Umlenkung der Kraftlinien dazu führt, dass die Spannung direkt am Rand der Verengung überhöht ist – sie ist nicht einfach Kraft pro (verkleinerte) Fläche, sondern tatsächlich noch größer. Diese sogenannte “Kerbwirkung” hat im Laufe der Geschichte zu vielen versagten Bauteilen geführt, damit umzugehen ist etwas, dass Maschinenbau-Studis deshalb lernen müssen. (Der Effekt ist um so schlimmer, je schärfer der Kerb ist, ganz extrem ist die Situation bei Rissen, das habe ich auch schon mal im Detail erklärt.)
In einem realen Bauteil (und die meisten Bauteile sind ja noch wesentlich komplizierter geformt als ein Gummiband, selbst mit Verengung) ist die Spannung also an jedem Ort eine andere. Weil man in der Mathematik Größen, die vom Ort abhängen, Felder nennt, spricht man deshalb auch von einem “Spannungsfeld”.
Zum Abschluss mal ein Beispiel aus meiner eigenen Forschung. Ihr seht die Spannung (genauer gesagt, die senkrechte Spannungskomponente S11) an der Grenzfläche zwischen einem Material und einer darüber liegenden Wärmedämmschicht. Die beiden haben unterschiedliche Wärmeausdehnungen, deshalb entstehen bei Temperaturänderung Spannungen:
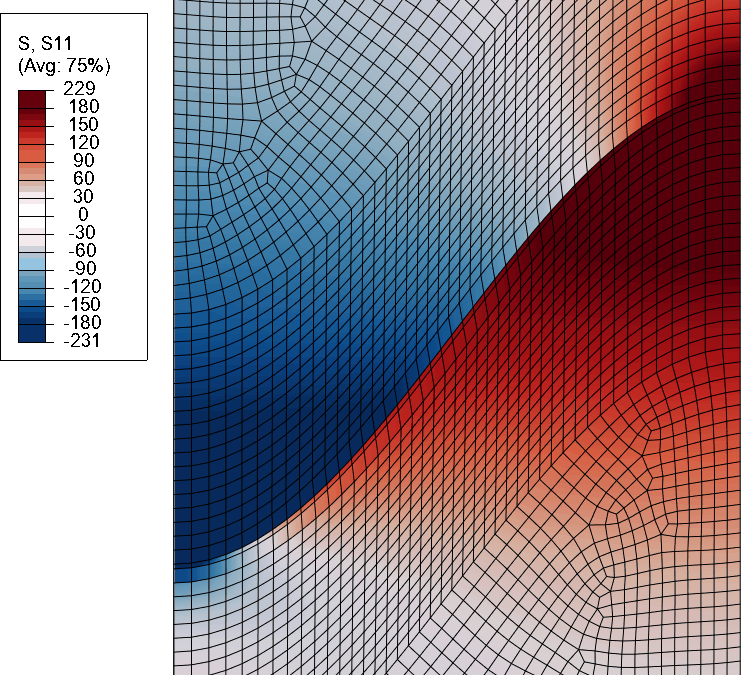
In rot sind hier Zugspannungen, in blau Druckspannungen, man sieht also, dass an der (gekrümmten) Grenze rechts oben im Bild Zugspannungen herrschen; hier könnte sich dann die Schicht ablösen.
Und warum ist das alles wichtig?
Die Spannung in einem Bauteil zu kennen, ist natürlich ziemlich wichtig, wenn ihr etwas konstruieren wollt. (Es sei denn, ihr macht es wie Calvins Vater…). Wenn ihr wisst, dass eure Legierung bei einer Spannung von 300 Newton pro Quadratmillimeter anfängt, sich plastisch zu verformen, dann könnt ihr die Spannung im Bauteil berechnen und sehen, ob sie irgendwo diesen Wert erreicht. (Aufmerksame LeserInnen fragen jetzt “Moment mal, die Spannung hat doch ne komplizierte Richtungsabhängigkeit und ich brauche 6 Zahlen, um sie vollständig zu beschreiben. Welche davon muss ich denn nehmen?” Das ist eine gute Frage. Ihr könnt dazu in Metallen folgendes tun: Ihr messt die kritische Spannung in eurem Material in einem Zugversuch, wo also die Spannung eine reine Zugspannung in einer Richtung ist. Wenn ihr einen komplizierten Spannungszustand mit seinen 6 Zahlen habt, dann könnt ihr den in eine spezielle mathematische Formel stopfen, die euch eine Zahl auswirft, die ihr mit dem kritischen Wert vergleichen könnt, den ihr im Zugversuch gemessen habt. In Keramiken ist die Situation anders, die sind vor allem rissempfindlich, da ist immer die maximale Zugspannung interessant.)
Und wie berechnet man die Spannung an jedem Punkt in einem Bauteil, also so ein Spannungsfeld? Das macht man heutzutage mit der sogenannten Finite-Element-Methode. Aufwändige (und teure) Computerprogramme können die Spannung im Bauteil berechnen, wenn ihr die Geometrie, die Lasten und alle weiteren Daten einfüttert, so wie in meinem Beispiel der Schicht. Wie das geht? Das erkläre ich euch gern ganz detailliert, fangt einfach an, bei uns an der TU Braunschweig Maschinenbau zu studieren und besucht meine “Praxisvorlesung Finite Elemente”.
PS: Dank an @bewitchedmind auf twitter für die Idee zu diesem Text (o.k., das hattest du wohl nicht erwartet…)






Kommentare (50)