Das Universum dehnt sich ja bekanntlich aus – und wie wir diese Woche gelernt haben, gab es dabei mit ziemlicher Sicherheit eine Zeit, in der diese Ausdehnung extrem schnell war. Aber was passiert eigentlich, wenn sich der Raum ausdehnt? Warum dehnt sich z.B. unser Sonnensystem nicht mit aus?
Die Ausdehnung des Universums wird ja gern mit folgenden Bildchen veranschaulicht:

Von Leipnizkeks, CC BY-SA 3.0, Link
Hier sieht man ein “flaches” Universum, in dem sich die Objekte immer weiter voneinander entfernen. Was an diesem Bild nicht so schön ist, ist, dass es so aussieht, als wäre der Punkt in der Mitte irgendwie speziell – aber das ist er nicht. Alternativ wird deswegen oft das Ballonbild verwendet:
Quelle: E. Siegel, Starts with a Bang
Man stellt sich die Objekte wie kleine Punkte vor, die auf der Oberfläche eines Ballons angeheftet sind und die sich dann alle voneinander entfernen.
Und das wirft natürlich folgende Frage auf: Wenn zwei Punkte am Anfang einen bestimmten Abstand zueinander haben und sich das Universum dann ausdehnt, dann vergrößert sich ja der Abstand zwischen ihnen. Wenn an jedem dieser Punkte ein Objekt sitzt, entfernen sich die beiden voneinander. Warum wird dann zum Beispiel unser Sonnensystem oder unsere Galaxis nicht mit expandiert?
Bei der Suche nach einer Antwort auf diese Frage bin ich nebenbei auf folgendes Filmzitat gestoßen:
Mrs Felix: Why don’t you do your homework?
Allen Felix: The Universe is expanding. Everything will fall apart, and we’ll all die. What’s the point?
Mrs Felix: We live in Brooklyn. Brooklyn is not expanding! Go do your homework.(from Annie Hall by Woody Allen)
Diese Frage wird im Internet an vielen Stellen diskutiert – allerdings sind die Erklärungen manchmal sehr problematisch. Meistens heißt es, dass die Kräfte, die zum Beispiel das Sonnensystem zusammenhalten, eben einfach größer sind als die Kraft, die die Objekte des Sonnensystems oder die Galaxien auseinandertreibt. In dieser Diskussion zum Beispiel wird das Ballonbild verwendet und die Galaxien mit Münzen. Die Kraft, die die Münzen zusammenhält, ist “größer als die Reibungskraft”. Die Galaxien werden nicht auseinandergetrieben, weil die zusammenhaltende Kraft der Galaxien (die Schwerkraft) größer ist als die Kraft, mit der sie durch die Expansion des Universums auseinangetrieben werden.
Ich gebe zu, dass ich das bisher auch immer so verstanden hatte. Dummerweise ist dieses Bild aber nicht wirklich richtig – es liefert eine falsche Vorstellung davon, welche Kräfte da wirken können. Ich habe das gestern gemerkt, als ich spaßeshalber ausrechnen wollte, wie groß die Kraft ist, mit der zwei Punkte im Universum durch die Expansion auseinandergetreiben werden – dummerweise kam immer Null heraus. Also wie denn nun?
Betrachten wir den einfachsten Fall: wir nehmen ein Universum, dass sich vollkommen gleichmäßig und mit zeitlich konstanter Rate ausdehnt. So eine Ausdehnung wird durch den sogenannten Hubble-Parameter beschrieben. Laut Wikipedia hat der den Wert
Was bedeutet das? Zwei Objekte, die sich in einer Entfernung von einem Megaparsec (1 Million Parsec, also etwa 3 Millionen Lichtjahre) befinden, entfernen sich mit einer Geschwindigkeit von etwa 74km/s voneinander. So jedenfalls die gängige Interpretation – die ist auch nicht falsch, aber ein bisschen irreführend. Tatsächlich ist es ja der Raum, der sich ausdehnt – man kann auch sagen: Zwischen den beiden Objekten entsteht neuer Raum, und zwar (in dieser Richtung) 74 Kilometer Raum pro Sekunde.
Klingt viel – aber ein Megaparsec ist auch ziemlich lang. Man kann den Hubble-Parameter auch umrechnen, wenn man sich erinnert, dass ein Megaparsec ja auch eine Längeneinheit ist. rechnet man das Megaparsec in Meter um, dann bekommt man (ebenfalls laut Wiki) den Wert 2,3·10−18 s−1.
Das mag auf den ersten Blick seltsam aussehen, weil die Dehnung die Einheit pro Sekunde hat – müsste da nicht eine Länge drin stecken? Es ist aber alles in Ordnung – eine doppelt so lange Strecke dehnt sich ja auch doppelt so viel, so dass man die Länge herauskürzen kann. (Alle IngenieurInnen kennen das – die Dehnung ist eine Größe ohne Einheit, weil es eine Längenänderung bezogen auf eine Ausgangslänge ist.) Eine beliebiges “Stück Raum” wächst also in einer Sekunde um das 2,3·10−18-fache.


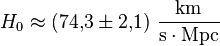





Kommentare (394)