In den Artikel meines 50tägigen Countdowns zum 50. Jubiläum der Mondlandung habe ich vor allem jede Menge Geschichten, Anekdoten, Bücher und ähnlich Vermischtes aufgegriffen und nur zwischendurch immer wieder mal über konkrete Wissenschaft geschrieben. Unter anderem deswegen, weil die Landung auf dem Mond zwar durchaus eine absolute wissenschaftliche und technische Meisterleistung war aber eben auch ein mindestens ebenso wichtiges historisches und kulturelles Ereignis. Aber ganz ohne Wissenschaft geht es nicht und auch nicht ohne Mathematik. Darum ist heute, bei Nummer “8” des Countdowns die Raketengrundgleichung das Thema.
Diese mathematische Formel ist – wie der Name nahelegt – die Grundlage des Raketenfluges. So sieht sie aus:
Sie beschreibt den Zusammenhang zwischen Masse und Geschwindigkeit einer Rakete und wurde 1903 von Konstantin Eduardowitsch Ziolkowski aufgestellt. Kein Wissenschaftler im engeren Sinn, sondern Mathelehrer in der russischen Provinz. Aber trotzdem derjenige, der die Grundlage für die moderne Raumfahrt geschaffen hat. Die Gleichung ist eigentlich recht simpel, aber trotzdem sehr tiefsinnig. Die Geschwindigkeit v der Rakete hängt, wie man in der Formel sehen kann, hauptsächlich von der Masse m ab. Was man aber auch sieht, und was vielleicht nicht gleich offensichtlich ist: m ist in dieser Gleichung eine Variable. Das heißt, die Masse der Rakete ändert sich im Laufe der Zeit und nur weil das passiert, kann sie fliegen!
Wie schnell eine Rakete ist, hängt davon ab mit welcher Geschwindigkeit (vG) sie die sogenannte “Stützmasse” ausstößt. Ganz vereinfacht gesagt: Je mehr und je schneller die Rakete hinten Masse ausstößt, desto schneller fliegt sie in die andere Richtung davon (das folgt aus der Impulserhaltung und dem dritten Newtonschen Gesetz). Alles will man natürlich unterwegs nicht loswerden; deswegen gibt es in der Formel auch den Term “m0”, die “Grundmasse” zu der unter anderem auch die Nutzlast gehört. Aber auch die Masse des Treibstoffs und die der Struktur selbst.
Das variable “m” in der Formel ist die “Restmasse” und je kleiner dieser Wert wird, desto höher kann die Endgeschwindigkeit sein die die Rakete haben kann. Und weil man die nicht beliebig verkleinern kann (irgendwas soll ja am Ende auch im All ankommen) muss man schauen, dass man davor möglichst viel los wird. Das ist einmal der Treibstoff, der ja verbrannt wird um möglichst hohe Werte für vG zu erreichen mit der die Verbrennungsprodukte ausgestoßen werden können. Und es bleibt die “Strukturmasse”, als das, aus dem die Rakete selbst besteht. Das ist auch der Grund, warum moderne Raketen aus “Stufen” aufgebaut sind. Ist der Treibstoff in einer solcher Stufe verbraucht, dann wird die gesamte Stufe abgeworfen um möglichst viele Masse loswerden zu können. Am Ende bleibt dann nur wenig übrig. Von den fast 3000 Tonnen die die Saturn-V-Rakete der NASA hatte mit der die Astronauten 1969 zum Mond flogen sind nur 133 Tonnen Nutzlast gewesen…
Natürlich ist die Raumfahrt mathematisch deutlich komplexer als diese eine Formel. Aber sie ist ein Anfang und man kann schon allein aus ihr einiges darüber lernen, wie man ins All gelangen kann…
———————————
Der komplette Countdown: 50 | 49 | 48 | 47 | 46 | 45 | 44 | 43 | 42 | 41 | 40 | 39 | 38 | 37 | 36 | 35 | 34 | 33 | 32 | 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 09 | 08 | 07 | 06 | 05 | 04 | 03 | 02 | 01 | 0


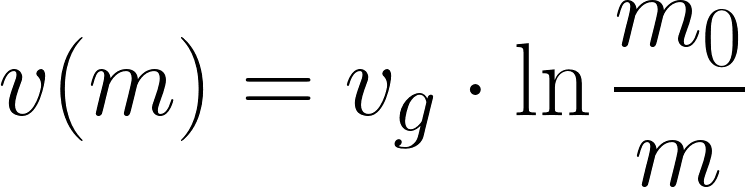











Kommentare (9)