Es sei denn natürlich, dass die Raumzeit gekrümmt ist. Den Effekt der Zeitdilatation durch die Höhe seht ihr in diesem Bild:
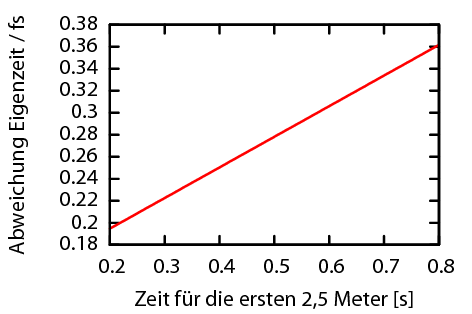
Auch hier ist auf der x-Achse wieder aufgetragen wann der Ball die ersten 2,5 Meter passiert hat. Wenn es nur diesen Effekt gäbe, dann wäre es für den Ball natürlich am besten, auf dem ersten Stück möglichst langsam unterwegs zu sein, weil er da weiter oben ist, wo die Zeit schneller läuft.
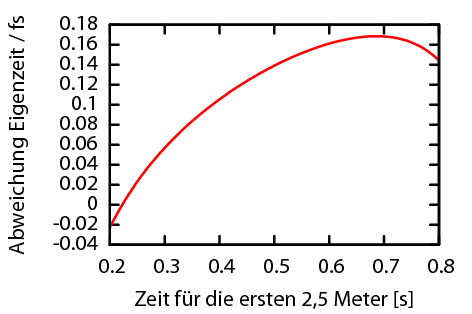
Da es aber beide Effekte gibt, müssen wir die beiden Kurven addieren. Dabei kommt das hier heraus:
Das Maximum liegt bei 0.686 Sekunden. Der Ball sollte also auf dem ersten Stück etwas langsamer sein, auf dem zweiten etwas schneller, so dass sich ein Kompromiss aus den beiden Effekten ergibt.
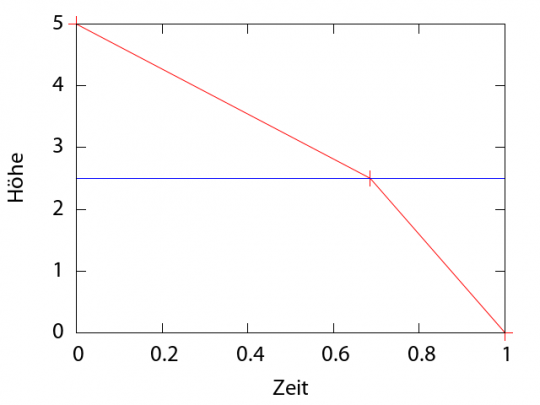
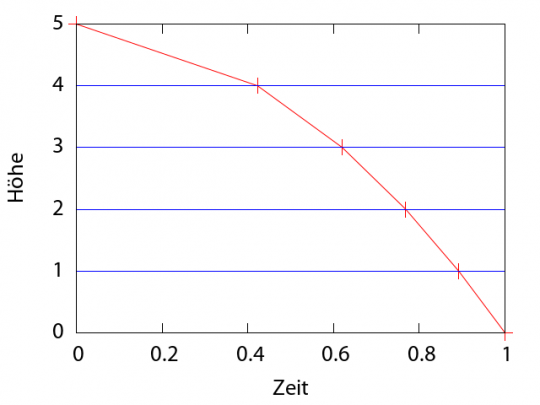
Die Weltlinie, die unser Ball beschreibt (in der wir also Höhe gegen Zeit auftragen) sieht dann so aus:
Sieht nicht ganz so aus wie die wirkliche Bewegung eines Balles, oder? Der fällt ja nicht mit stückweise konstanter Geschwindigkeit.
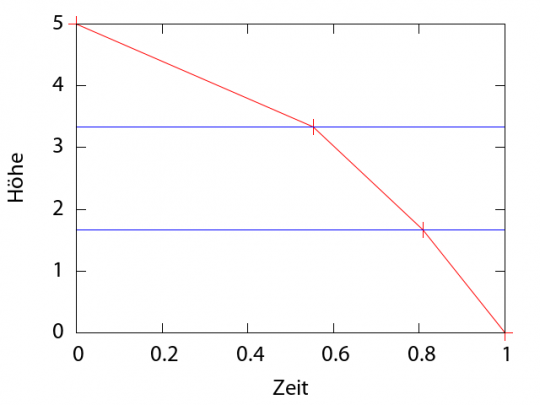
Allerdings war unsere Annahme, dass wir zwei Stücke mit konstanter Geschwindigkeit haben, natürlich sehr grob. Vielleicht sollten wir besser drei Stücke mit jeweils konstanter Geschwindigkeit nehmen? Dann kommt das hier dabei heraus:
Oder wie wäre es mit 5 Stücken?
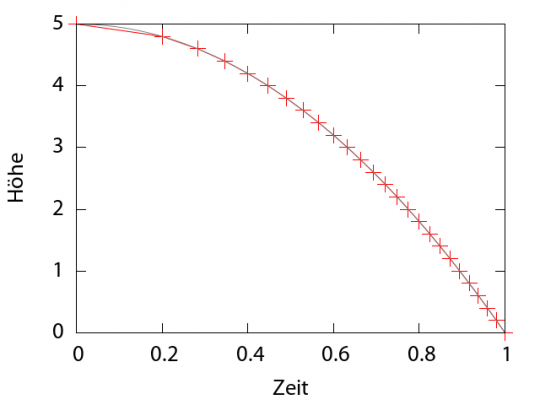
Und wenn wir gar 25 Stücke nehmen, dann bekommen wir eine Bahn, die der tatsächlichen (ebenfalls eingezeichnet) schon sehr nahe kommt:
Es ergibt sich also die parabelförmige Kurve, die ihr vermutlich mal im Physikunterricht kennengelernt habt. Damals hat man euch aber etwas von “Schwerkraft” und “Beschleunigung” erzählt – tatsächlich folgt der Ball aber einfach der Linie mit der maximalen Eigenzeit im Raum, weil das die geradeste Linie ist, die es gibt.
PS: Nebenbei zeigt diese Rechnung mal wieder, dass das von vielen so geliebte Gummituchmodell Quatsch ist: Dort ist ja der Raum gekrümmt – aber die Raumkrümmung ist für frei fallende Teilchen im “Schwerefeld” der Erde ziemlich irrelevant, die wird nur relevant, wenn sich Objekte mit nahezu Lichtgeschwindigkeit bewegen oder wenn die Raumkrümmung sehr groß wird, wie z.B. bei schwarzen Löchern.
PPS: Die notwendigen Formeln zum Berechnen der Effekte findet ihr am Ende dieses Artikels; die Optimierung habe ich mit einem kleinen Pythonprogramm (mit einem Nelder-Mead-Simplex-Algorithmus, den hatte ich eh gerade bei der Arbeit gebraucht) gemacht. Falls jemand das (grueselig zusammengehackte) Programm haben will, schickt mir ne mail…
PPPS: Auf Wunsch habe ich das Ganze jetzt bei github hochgeladen:






Kommentare (32)