StartseiteGeograffitico

Die diskriminierte Addition

Von / 13. Mai 2013 / 9 Kommentare
Mehr

Heute geht es erst mal nur um Regeln und deren Anwendung beziehungsweise deren Verständnis. Nehmen wir mal folgende, simple Rechnung:

7 – 1 x 0 + 3 : 3

Die korrekte Lösung ist 1, nicht wahr? Denn wenn ich nachrechne, dann kommt genau diese 1 raus:
7 – 1 = 6
↓
6 x 0 = 0
↓
0 + 3 = 3
↓
3 : 3 = 1!

Und das behaupte nicht nur ich – folgende “Studie” beweist, dass ich Recht habe:
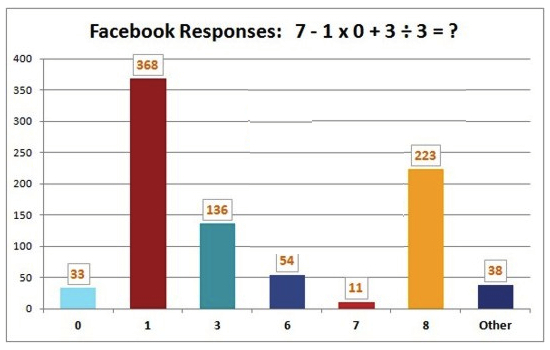Rechnungsbeispiel(Quelle)
Die größte Gruppe aller Antwortenden ist sicher, dass 1 das korrekte Ergebnis ist. Der Rest ist so verstreut, dass man davon ausgehen kann, dass die halt nicht rechnen können …

Wie bitte? 8 soll richtig sein? Weil Punktrechnung vor Strichrechnung geht, Multiplikationen und Subtraktionen also wichtiger sind als Additionen und Subtraktionen? Das ist eine Diskriminierung von Rechenoperationen! Außerdem ist das ist doch viel zu kompliziert – es wäre viel einfacher, wenn nach der Reihenfolge des Erscheinens gerechnet würde.

Soviel erst mal heute als Denkanregung. In den nächsten Tagen werde ich meine Gedanken zur Zeichensetzung und den Rechenregeln weiterspinnen …

flattr this!

Stichworte: ,
Mehr

Kommentare (9)

  1. #1 rolak
    13. Mai 2013

    Diese Diskriminierung erklärt sich aus alter™ Tradition: So steht mancher Punkt der Gesetzgebung weit über dem Treiben auf dem Strich, ist mithin wichtiger und geht somit vor (nicht wie eine Uhr).

  2. #2 jochen
    13. Mai 2013

    Und was mache ich, wenn ich von rechts nach links lese?

    3:3=1

    1+0=1

    1*1=1

    1-7=-6

    Ich halte links nach rechts Leserichtungsbevorzugung für diskriminierend. Gleiches Recht für alle Richtungen!

  3. #3 dg
    13. Mai 2013

    Ich vermute mal, wie die meisten mathematischen Definitionen/Notationen hat sich auch diese durchgesetzt, weil sie am sinnvollsten ist.
    Bei so abstrakten Aufgaben ist das natürlich schwer zu sehen, aber geh mal auf den Markt und kauf 5kg Äpfel für 1,99/kg, 2 Bund Möhren für 0,99€/Bund und 3 Bananen für jeweils 0,30, macht
    5*1,99+2*0,99+3*0,30 vs
    (5*1,99)+(2*0,99)+(3*0,30)

    Und so vom Gefühl her laufen einem in der Natur eher Summen von Produkten als Produkte von Summen über den Weg, insofern ist es sinnvoll, den Standardfall mit möglichst wenig Klammern und zusätzlichem Ballast schreiben zu können. Und das bedeutet dann eben “Punkt vor Strich”.

    Wer ganz ohne Klammern und Diskriminierung auskommen will benutzt dann halt polnische Notation, aber das will üblicherweise dann auch niemand von denen, die oben “1” getippt haben…

  4. #4 Herr Senf
    13. Mai 2013

    Mit 2,333… kann sich keiner verrechnen, oder?
    7 – 1 x 2,333… + 3 : 3 = 5,666… egal wie!
    Das Problem ist die “0” nebst allen anderen Zahlen.
    Im axiomatischen Zahlensystem sollen alle Rechenregeln universell gelten (Permanenzprinzip) und für den “Verbraucher” möglichst intuitiv sein, so wie sie sich geschichtlich “von alleine” entwickelt haben. Das geht aber nur mit einigen Beschränkungen wie “Punkt vor Strich”. Anderenfalls würde das System komplizierter, für viele nicht mehr überschaubar, also kontraintuitiv. Auch in der Mathematik greift Ockhams Rasiermesser – einfach bleiben.

  5. #5 michael
    13. Mai 2013

    > Multiplikationen und Subtraktionen also wichtiger sind als Additionen und Subtraktionen

    Der Satz ist zwar nicht falsch, aber die Division wird diskriminiert .

  6. #6 anoynymous
    13. Mai 2013

    Als entschiedener Diskriminierungsgegner und Mathematiker fordere ich die flächendeckende Einführung der polnischen Notation.

    https://en.wikipedia.org/wiki/Polish_notation

    Obige Gleichung wird somit (unter Beachtung der Standardregeln) zu:

    – 7 + x 1 0 : 3 3

    Alles klar?

  7. #7 Constantin
    14. Mai 2013

    Ich hab eher an die Umgekehrte Polnische Notation gedacht!

  8. #8 michael
    15. Mai 2013

    @Juergen

    Git es einen Grund, warum der Blog eintrag von Georg zur Beschneidung nicht unter den Kategorien Politik oder Kultur oder .. zu finden ist ?

  9. #9 Die Mühe beim Sprechen – Geograffitico
    15. Mai 2013

    […] ein paar Tagen hatte ich hier einen Köder ausgeworfen: Leider hat sich niemand meiner Forderung anschließen wollen, simple Grundregeln der […]