Wenn es um höhere mathematische Beweisführung geht, bin ich zugegebener Maßen weit außerhalb meiner sicheren Schwimmtiefe. Darum habe ich erst mal gezögert, mich zu der Meldung zur Bestätigung von Gödels ontologischem Gottesbeweis zu äußern. Andererseits ist es zwar eine Sache, mathematische Beweise zu führen – eine ganz andere aber, deren Annahmen und Resultate auf ihre Plausibilität zu prüfen. Da genügt manchmal schon eine ziemlich normale Argumentationsfähigkeit. Ich habe mir also mal das Paper Formalization, Mechanization and Automation of Gödel’s Proof of God’s Existence angeschaut, das von Christoph Benzmüller und Bruno Woltenzlogel Paleo angeschaut. Und nein, ich maße mir nicht an, auch nur eine einzige Zeile in dem zwei Seiten langen Paper anzuzweifeln – ich bin mir sogar absolut sicher, dass die beiden Wissenschaftler (und vor allem ihr Computer, der – wie ich dem Hinweis auf “our computer-assisted formalizations” entnehme – einen Großteil der Arbeit erledigt hat) ganz korrekt vorgegangen sind. Doch die Existenz Gottes ist damit natürlich nicht bewiesen.
Im Prinzip sieht Gödels ontologischer Gottesbeweis so aus (ich zitiere das mal visuell direkt aus dem Paper, da ich nicht sicher bin, ob unsere LaTeX-Kapazitäten in der Blogsoftware mal wieder spinnen oder nicht):
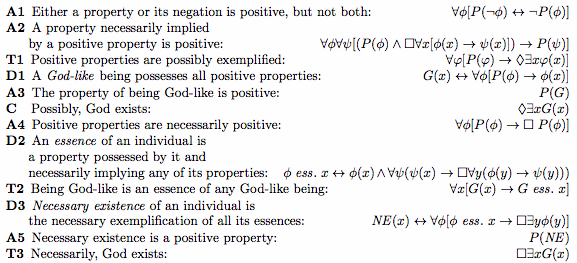
Diesen Argumentationsaufbau wiederum haben die Autoren den Aufzeichnungen des Mathematikers und Computerwissenschaftlers Dana Scott entnommen, der in Princeton bei Gödel studiert und sich nach einem Gespräch mit Gödel über diesen Beweis (den der Professor bis dahin für sich behalten hatte) notiert; das Verdienst des aktuellen Papers ist, dass es einige Lücken geschlossen und die ganze Chose dann auch durchgerechnet hat.
Dazu muss man aber wissen, dass dies nur deshalb funktioniert, weil die Axiome – im oberen Schema mit A markiert – dabei nicht in Zweifel gezogen werden. Und da scheitert schon die erste Aussage – “Entweder eine Eigenschaft oder ihre Verneinung ist positiv, aber nicht beides” – and der Realität. Eigenschaften sind meist ambivalent und nur in ihrem jeweiligen Kontext positiv oder negativ: Ich freue mich über ein warmes Wohnzimmer im Winter, aber wenn mir der Champagner warm serviert wird, verdirbt’s mir den Spaß. Großzügigeit kann gut sein – oder Selbstausbeutung. Nicht mal bei Zahlen würde dieses Axiom hinhauen: Sicher gibt es positive und negative Zahlen, aber was ist mit der Null? Und was ist, wenn die negative Zahl am Ende meiner Stromrechnung steht? Dann heißt das, mein Stromversorger schuldet mir Geld – und das ist positiv (für mich, jedenfalls).
Ich will diesen Beweis jetzt nicht trivialisieren – aber es ist offensichtlich, dass diese Axiome nur eine interne Bedeutung haben: Sie sind die Voraussetzungen, unter denen sich der Beweis führen lässt, aber das sagt nichts darüber aus, ob diese Voraussetzungen in der realen Welt eintreffen. Im Schnelldurchgang läuft die Argumentation also so:
• Eigenschaften sind entweder gut oder schlecht, aber nicht beides zugleich.
• Eigenschaften, die Voraussetzungen für eine positive Eigenschaft sind, sind selbst positiv.
• Ein gottgleiches Wesen muss alle bestehenden positiven Eigenschaften besitzen (will heißen: Es gibt keine positive Eigenschaft, die dieses gottgleiche Wesen nicht besitzt).
• Gottgleich zu sein ist eine positive Eigenschaft.
Hier überspringe ich mal ein paar Schritte, aber es läuft dann darauf hinaus, dass
• “Necessary existence”, was ich hier mal mit “Notwendigkeit der Existenz” übersetzen werde, ist eine positive Eigenschaft.
Ergo: Gott besitzt die Eigenschaft der “necessary existence”, muss also notweniger Weise existieren.
Wie gesagt, als formal logisches Konstrukt ist das sicher schlüssig – aber es wäre auch dann noch schlüssig, wenn Gott nicht existiert.





Kommentare (132)