Unendlich viele geschlossene geodätische Kurven.

Wir hatten in den letzten Wochen über kritische Punkte differenzierbarer Funktionen auf einer Fläche geschrieben und verschiedene Methoden zur Abschätzung ihrer Anzahl. Diese Methoden lassen sich auch anwenden zur Bestimmung der Anzahl geschlossener geodätischer Kurven auf einer Fläche – bzw. zum Beweis, dass es auf Tori, Brezeln und Flächen mit mehreren Henkeln immer unendlich viele geschlossene Geodäten gibt, egal welche Metrik man nimmt.

Reminder: Abschätzungen für die Anzahl kritischer Punkte
In TvF 218 hatten wir über die Lusternik-Schnirelman-Theorie geschrieben, mit der man die Mindestanzahl kritischer Punkte für differenzierbare Funktionen auf einer Fläche bestimmen kann.
Bessere Abschätzungen bekam man für sogenannte Morse-Funktionen, also Funktionen bei denen alle kritischen Punkte nichtdegeneriert sind. Mittels Morsetheorie beweist man (TvF 217) eine untere Schranke für die Anzahl der kritischen Punkte durch die Summe der Betti-Zahlen (d.h. der Dimensionen der Homologie-Gruppen) der Fläche. (In TvF 209 hatten wir mal erwähnt, dass in gewisser Weise ‘fast alle’ Funktionen Morse-Funktionen sind: jede Funktion lässt sich durch eine kleine Störung zu einer Morse-Funktion machen.)

Auf einer Fläche mit g Henkeln bekam man damit, daß jede Morse-Funktion mindestens 2g+2 kritische Punkte haben muß. Diese Abschätzung durch 2g+2 (die Summe der Betti-Zahlen) ist wesentlich besser als die durch die Lusternik-Schnirelman-Invariante, mit der man ja nur bekam, dass es (auf Flächen mit mindestens einem Henkel) immer 3 kritische Punkte geben muss.
Man fragt sich vielleicht, warum man mit einer einschränkenden Voraussetzung eine bessere Abschätzung bekommt. Die Erklärung ist, dass es, wenn man eine differenzierbare Funktion durch eine kleine Störung zu einer Morse-Funktion macht, passieren kann, dass ein degenerierter kritischer Punkt sich in mehrere nichtdegenerierte kritische Punkte der Morse-Funktion auflöst.
Ein Beispiel: das Bild unten zeigt rechts f(x)=x³, was keine Morse-Funktion ist, weil es einen degenerierten kritischen Punkt hat, und links eine durch Störung von x³ entstandene Morse-Funktion, die aber statt des einen entarteten jetzt zwei nicht-entartete kritische Punkte hat:

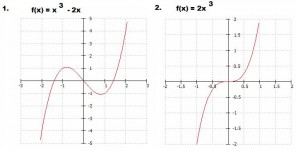
Auch wenn die Morse-Funktion auf einer Fläche mindestens 2g+2 kritische Punkte hat, sagt das also noch nichts über die Anzahl der kritischen Punkte der ursprünglichen Funktion.

Geschlossene Geodäten

Die ursprüngliche Motivation für die Theorien von Morse und wohl auch von Lusternik-Schnirelman war die Suche nach geschlossenen Geodäten. Wir hatten letzte Woche über den auf Lusternik und Schnirelman zurückgehenden Satz geschrieben, dass es zu jeder Metrik auf der Sphäre mindestens 3 geschlossene Geodäten gibt.

Geschlossene Geodäten als kritische Punkte des Energie-Funktionals

Was haben geschlossene Geodäten mit kritischen Punkten zu tun?
Man kann geschlossene Geodäten als kritische Punkte auf einem gewissen unendlich-dimensionalen Raum bekommen. Nämlich, zu der gegebenen Fläche M betrachtet man den sogenannten Schleifenraum, d.h. den Raum Λ(M) aller absolutstetigen Abbildungen S¹—>M mit quadrat-integrierbaren Ableitungen. (Das ist ein unendlich-dimensionaler Raum.)

Die Elemente dieses Raumes sind Abbildungen f:S¹—>M, also geschlossene Kurven, und zu jeder solchen Kurve kann man ihre Energie E(f) betrachten, definiert als 1/2 x Integral (über S¹) von IIf'(t)II²dt. Das definiert eine Funktion E:Λ(M)—>R und man kann leicht beweisen, dass die (nach Bogenlänge parametrisierten) geschlossenen Geodäten gerade die kritischen Punkte dieser Funktion sind.
Man kann also versuchen, Morse-Theorie zu benutzen um die Anzahl geschlossener Geodäten zu bestimmen. Natürlich muss man beachten, dass man hier Morse-Theorie auf einem unendlich-dimensionalen Raum betreibt, aber das ist letztlich kein wirkliches Problem. (Tatsächlich kann man diesen unendlich-dimensionalen Raum gut durch endlich-dimensionale Räume approximieren. Die Energie erfüllt auch die Palais-Smale-Bedingung, so daß man wie im endlich-dimensionalen Fall Morse-Theorie betreiben kann.)

Wenn die Energie E eine Morse-Funktion ist, dann bekommt man sofort, dass die Anzahl der kritischen Punkte mindestens gleich der Summe der Betti-Zahlen (des Schleifenraums!) sein muss, mit anderen Worten: die Anzahl der geschlossenen Geodäten auf M ist mindestens Σ_ib_i(ΛM).

Es ist a priori natürlich nicht so, dass diese Ungleichung auch für völlig beliebige Metriken gilt – wir hatten ja oben Beispiele gesehen, wo Funktionen, die keine Morse-Funktionen sind, deutlich weniger kritische Punkte haben können.