Unendlich viele geschlossene geodätische Kurven.

Wir hatten in den letzten Wochen über kritische Punkte differenzierbarer Funktionen auf einer Fläche geschrieben und verschiedene Methoden zur Abschätzung ihrer Anzahl. Diese Methoden lassen sich auch anwenden zur Bestimmung der Anzahl geschlossener geodätischer Kurven auf einer Fläche – bzw. zum Beweis, dass es auf Tori, Brezeln und Flächen mit mehreren Henkeln immer unendlich viele geschlossene Geodäten gibt, egal welche Metrik man nimmt.

Reminder: Abschätzungen für die Anzahl kritischer Punkte
In TvF 218 hatten wir über die Lusternik-Schnirelman-Theorie geschrieben, mit der man die Mindestanzahl kritischer Punkte für differenzierbare Funktionen auf einer Fläche bestimmen kann.
Bessere Abschätzungen bekam man für sogenannte Morse-Funktionen, also Funktionen bei denen alle kritischen Punkte nichtdegeneriert sind. Mittels Morsetheorie beweist man (TvF 217) eine untere Schranke für die Anzahl der kritischen Punkte durch die Summe der Betti-Zahlen (d.h. der Dimensionen der Homologie-Gruppen) der Fläche. (In TvF 209 hatten wir mal erwähnt, dass in gewisser Weise ‘fast alle’ Funktionen Morse-Funktionen sind: jede Funktion lässt sich durch eine kleine Störung zu einer Morse-Funktion machen.)

Auf einer Fläche mit g Henkeln bekam man damit, daß jede Morse-Funktion mindestens 2g+2 kritische Punkte haben muß. Diese Abschätzung durch 2g+2 (die Summe der Betti-Zahlen) ist wesentlich besser als die durch die Lusternik-Schnirelman-Invariante, mit der man ja nur bekam, dass es (auf Flächen mit mindestens einem Henkel) immer 3 kritische Punkte geben muss.
Man fragt sich vielleicht, warum man mit einer einschränkenden Voraussetzung eine bessere Abschätzung bekommt. Die Erklärung ist, dass es, wenn man eine differenzierbare Funktion durch eine kleine Störung zu einer Morse-Funktion macht, passieren kann, dass ein degenerierter kritischer Punkt sich in mehrere nichtdegenerierte kritische Punkte der Morse-Funktion auflöst.
Ein Beispiel: das Bild unten zeigt rechts f(x)=x³, was keine Morse-Funktion ist, weil es einen degenerierten kritischen Punkt hat, und links eine durch Störung von x³ entstandene Morse-Funktion, die aber statt des einen entarteten jetzt zwei nicht-entartete kritische Punkte hat:

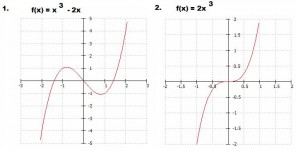
Auch wenn die Morse-Funktion auf einer Fläche mindestens 2g+2 kritische Punkte hat, sagt das also noch nichts über die Anzahl der kritischen Punkte der ursprünglichen Funktion.

Geschlossene Geodäten

Die ursprüngliche Motivation für die Theorien von Morse und wohl auch von Lusternik-Schnirelman war die Suche nach geschlossenen Geodäten. Wir hatten letzte Woche über den auf Lusternik und Schnirelman zurückgehenden Satz geschrieben, dass es zu jeder Metrik auf der Sphäre mindestens 3 geschlossene Geodäten gibt.

Geschlossene Geodäten als kritische Punkte des Energie-Funktionals

Was haben geschlossene Geodäten mit kritischen Punkten zu tun?
Man kann geschlossene Geodäten als kritische Punkte auf einem gewissen unendlich-dimensionalen Raum bekommen. Nämlich, zu der gegebenen Fläche M betrachtet man den sogenannten Schleifenraum, d.h. den Raum Λ(M) aller absolutstetigen Abbildungen S¹—>M mit quadrat-integrierbaren Ableitungen. (Das ist ein unendlich-dimensionaler Raum.)

Die Elemente dieses Raumes sind Abbildungen f:S¹—>M, also geschlossene Kurven, und zu jeder solchen Kurve kann man ihre Energie E(f) betrachten, definiert als 1/2 x Integral (über S¹) von IIf'(t)II²dt. Das definiert eine Funktion E:Λ(M)—>R und man kann leicht beweisen, dass die (nach Bogenlänge parametrisierten) geschlossenen Geodäten gerade die kritischen Punkte dieser Funktion sind.
Man kann also versuchen, Morse-Theorie zu benutzen um die Anzahl geschlossener Geodäten zu bestimmen. Natürlich muss man beachten, dass man hier Morse-Theorie auf einem unendlich-dimensionalen Raum betreibt, aber das ist letztlich kein wirkliches Problem. (Tatsächlich kann man diesen unendlich-dimensionalen Raum gut durch endlich-dimensionale Räume approximieren. Die Energie erfüllt auch die Palais-Smale-Bedingung, so daß man wie im endlich-dimensionalen Fall Morse-Theorie betreiben kann.)

Wenn die Energie E eine Morse-Funktion ist, dann bekommt man sofort, dass die Anzahl der kritischen Punkte mindestens gleich der Summe der Betti-Zahlen (des Schleifenraums!) sein muss, mit anderen Worten: die Anzahl der geschlossenen Geodäten auf M ist mindestens Σ_ib_i(ΛM).

Es ist a priori natürlich nicht so, dass diese Ungleichung auch für völlig beliebige Metriken gilt – wir hatten ja oben Beispiele gesehen, wo Funktionen, die keine Morse-Funktionen sind, deutlich weniger kritische Punkte haben können.

Bemerkenswerterweise gibt es aber einen Satz von Gromoll-Meyer, der eine Aussage für völlig beliebige Metriken (auf denen die Energie evtl. keine Morse-Funktion ist) liefert:
wenn die Folge b_i(ΛM) unbeschränkt ist, dann gibt es auf M unendlich viele geschlossene Geodäten.

Damit hat man jetzt eine rein topologische Bedingung und man kann mit topologischen Methoden, insbesondere rationaler Homotopietheorie, untersuchen, wann diese Bedingung erfüllt ist. Die grundlegende Arbeit dazu ist “The homology theory of the closed geodesic problem” von Vigué-Poirrier und Sullivan, es gibt aber viele weitere Resultate. In der Arbeit von Sullivan und Vigué-Poirrier war bewiesen worden, dass die Bedingung “b_i(ΛM) unbeschränkt” aus dem Gromoll-Meyer-Theorem dann und nur dann erfüllt ist, wenn die Kohomologiealgebra von M mindestens zwei Erzeuger hat.

Insbesondere für alle Flächen mit mindestens einem Henkel gibt es (was allerdings für Flächen auch schon vorher bekannt war) zu jeder Metrik unendlich viele geschlossene Geodäten.

Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16, Teil 17, Teil 18, Teil 19, Teil 20, Teil 21, Teil 22, Teil 23, Teil 24, Teil 25, Teil 26, Teil 27, Teil 28, Teil 29, Teil 30, Teil 31, Teil 32, Teil 33, Teil 34, Teil 35, Teil 36, Teil 37, Teil 38, Teil 39, Teil 40, Teil 41, Teil 42, Teil 43, Teil 44, Teil 45, Teil 46, Teil 47, Teil 48, Teil 49, Teil 50, Teil 51, Teil 52, Teil 53, Teil 54, Teil 55, Teil 56, Teil 57, Teil 58, Teil 59, Teil 60, Teil 61, Teil 62, Teil 63, Teil 64, Teil 65, Teil 66, Teil 67, Teil 68, Teil 69, Teil 70, Teil 71, Teil 72, Teil 73, Teil 74, Teil 75, Teil 76, Teil 77, Teil 78, Teil 79, Teil 80, Teil 81, Teil 82, Teil 83, Teil 84, Teil 85, Teil 86, Teil 87, Teil 88, Teil 89, Teil 90, Teil 91, Teil 92, Teil 93, Teil 94, Teil 95, Teil 96, Teil 97, Teil 98, Teil 99, Teil 100, Teil 101, Teil 102, Teil 103, Teil 104, Teil 105, Teil 106, Teil 107, Teil 108, Teil 109, Teil 110, Teil 111, Teil 112, Teil 113, Teil 114, Teil 115, Teil 116, Teil 117, Teil 118, Teil 119, Teil 120, Teil 121, Teil 122, Teil 123, Teil 124, Teil 125, Teil 126, Teil 127, Teil 128, Teil 129, Teil 130, Teil 131, Teil 132, Teil 133, Teil 134, Teil 135, Teil 136, Teil 137, Teil 138, Teil 139, Teil 140, Teil 141, Teil 142, Teil 143, Teil 144, Teil 145, Teil 146, Teil 147, Teil 148, Teil 149, Teil 150, Teil 151, Teil 152, Teil 153, Teil 154, Teil 155, Teil 156, Teil 157, Teil 158, Teil 159, Teil 160, Teil 161, Teil 162, Teil 163, Teil 164, Teil 165, Teil 166, Teil 167, Teil 168, Teil 169, Teil 170, Teil 171, Teil 172, Teil 173, Teil 174, Teil 175, Teil 176, Teil 177, Teil 178, Teil 179, Teil 180, Teil 181, Teil 182, Teil 183, Teil 184, Teil 185, Teil 186, Teil 187, Teil 188, Teil 189, Teil 190, Teil 191, Teil 192, Teil 193, Teil 194, Teil 195, Teil 196, Teil 197, Teil 198, Teil 199, Teil 200, Teil 201, Teil 202, Teil 203, Teil 204, Teil 205, Teil 206, Teil 207, Teil 208, Teil 209, Teil 210, Teil 211, Teil 212, Teil 213, Teil 214, Teil 215, Teil 216, Teil 217, Teil 218, Teil 219, Teil 220