Der Wege-Raum.
In den letzten Wochen hatten wir die Anzahl geschlossener Geodäten auf Flächen diskutiert.
Viel allgemeiner kann man natürlich auch diskutieren, wie der Raum aller Wege (zwischen 2 Punkten p und q) auf einer Fläche aussieht.
Das ist eine topologische Frage, aber um sie zu beantworten wird man als Hilfsmittel eine Riemannsche Metrik benutzen. (Eines der wiederkehrenden Themen in dieser Reihe ist ja der Nutzen der Geometrisierung, also von Metriken konstanter Krümmung, zur Beantwortung rein topologischer Fragen. Auch bei der Untersuchung des Wege-Raums wird sich wieder die Nützlichkeit ‘schöner Metriken’ zeigen.)
Wir haben also eine Fläche F und für zwei Punkte p,q interessieren wir uns für die Topologie von ΩF, dem Raum aller (glatten) Wege, d.h. aller (beliebig oft) differenzierbaren Abbildungen γ:[0,1]—>F mit γ(0)=p,γ(1)=q.
(Die Topologie des Wegeraums hängt nicht davon ab, welche Punkte p,q man gewählt hat. Sie hängt auch nicht davon ab, ob man differenzierbare oder nur stetige Abbildungen zulässt: Milnor hat bewiesen, dass beide Wegeräume homotopie-äquivalent zueinander sind. Für Beweise mittels Morse-Theorie braucht man aber differenzierbare Wege.)
Wir hatten ja letztes Mal gesagt, dass man zu einer gegebenen Metrik auf der Fläche das Energiefunktional auf dem Wegeraum definieren kann, welches jedem Weg γ das Integral von IIγ'(t)IIdt/2 zuordnet.
(Letzte Woche hatten wir das Energiefunktional nur für geschlossene Wege betrachtet. Dieselbe Definition geht aber auch für Wege von p nach q.)
Die Geodäten waren gerade die kritischen Punkte dieses Energie-Funktionals.
Laut Morse-Theorie ist die Mannigfaltigkeit (in diesem Fall ΩF) homotopie-äquivalent zu einem Zellkomplex, dessen Zellen den kritischen Punkten (in diesem Fall den Geodäten auf F) entsprechen, wobei die Dimension einer Zelle jeweils der Index des entsprechenden kritischen Punktes ist.
Man muss also wissen, wie man den Index einer Geodäte (als kritischer Punkt des Energie-Funktionals) bestimmt. Dafür brauchen wir den Begriff “konjugierte Punkte”:
Konjugierte Punkte
Wenn man eine Geodäte γ hat, dann kann man sich fragen, ob diese sich deformieren lässt, also ob es wie im Bild unten eine “Homotopie” H(t,s) mit H(t,0)=γ(t) für alle t gibt, so dass für jedes S die Kurve H(t,S) eine Geodäte ist.
Der Punkt γ(T) heisst nun konjugiert zu γ(0) entlang γ, wenn es eine solche von einem Parameter s abhängende Homotopie H(t,s) gibt, die γ(0) und γ(t) festlässt, d.h. H(0,s)=γ(0) und H(T,s)=γ(T) für alle s.
Das Bild unten links zeigt, dass antipodale Punkte auf der Sphäre zueinander konjugiert sind. Andererseits kann es, wie die Bilder rechts zeigen, durchaus Geodäten mit gemeinsamen Anfangs-und Endpunkten geben, die sich nicht durch eine Homotopie ineinander überführen lassen. In diesem Fall sind die Endpunkte also nicht zueinander konjugiert.
Der Begriff der konjugierten Punkte lässt sich nun anwenden in der Morse-Theorie des Wegeraums.
Wir betrachten wieder das Energiefunktional E auf ΩF, dem Raum aller Wege, die zwei (fest gewählte) Punkte p und q auf der Fläche F verbinden. Die Geodäten waren die kritischen Punkte des Energiefunktionals E (das von einer fest gewählten Metrik abhängt).
Satz 15.1. in “Morse Theory” sagt dann: der Index des Energiefunktionals E:ΩF—>R in einem kritischen Punkt (d.h. in einer Geodäte γ) ist gerade die Anzahl von Punkten γ(t), die zu γ(0) entlang γ konjugiert sind.
Was sagt das nun über die Topologie des Wegeraums?
In TvF 214 hatten wir gesehen, dass man Morse-Theorie benutzen kann, um einen Raum in Zellen zu zerlegen. Wenn f:M—>R eine Morse-Funktion ist, dann ist M homotopie-äquivalent zu einem Zellkomplex, der eine k-dimensionale Zelle zu jedem kritischen Punkt vom Index k der Morse-Funktion f hat. Das funktioniert zwar nach klassischer Morse-Theorie erstmal nur für kompakte endlich-dimensionale Mannigfaltigkeiten, aber der (unendlich-dimensionale) Wegeraum lässt sich durch endlich-dimensionale Mannigfaltigkeiten approximieren und man kann dann die analoge Aussage auch für das Energiefunktional beweisen:
ΩF ist homotopie-äquivalent zu einem Zellkomplex, wobei (nach Wahl einer Riemannschen Metrik auf F) jede Zelle einer Geodäte γ auf F (von p nach q) entspricht und die Dimension der Zelle jeweils die Anzahl der zu γ(0) konjugierten Punkte auf γ ist.
(Dieser Satz stimmt allerdings nur, falls p und q nicht konjugiert sind. Letztere Bedingung kann man aber durch eine kleine Störung der Metrik immer erreichen.)
Der Wegeraum der Sphäre
Wir betrachten die runde Sphäre, also die Sphäre mit einer Metrik konstanter Krümmung. Die Geodäten sind die Großkreise.
Dann sind jeweils die antipodalen Punkte (und nur diese) zueinander konjugiert.
Seien nun p und q zwei nicht-konjugierte (also nicht-antipodale) Punkte. Wieviele Geodäten von p nach q gibt es?
Zunächst gibt es die kürzeste Verbindung auf dem Großkreis. Die enthält den zu p konjugierten (antipodalen) Punkt nicht, hat also Index 0.
Die längere Hälfte des Großkreises ist ebenfalls eine Geodäte. Sie durchläuft den antipodalen Punkt einmal, hat also Index 1.
Dann kann man natürlichen auch den Großkreis einmal ganz durchlaufen und anschließend von p nach q. Dabei hat man zunächst den zu p antipodalen Punkt und danach auch noch einmal p selbst (was dann ebenfall ein konjugierter Punkt ist) durchlaufen und je nachdem ob es sich bei letzten Drittel um die kürzere oder längere Verbindung von p nach q handelt, hat man 2 oder 3 konjugierte Punkte. In einem Fall also Index 2, im anderen Index 3.
Und wenn man den Großkreis erst zweimal ganz durchläuft und anschließend von p nach q, dann hat man 4 bzw. 5 konjugierte Punkte etc.pp.
Also: ΩS2 hat jeweils eine Zelle in Dimension 0,1,2,3,4,5,….
Der Wegeraum der Flächen höheren Geschlechts
Auf Flächen höheren Geschlechts gibt es Metriken mit Krümmung ≤0, z.B. auf dem Torus gibt es flache Metriken (Krümmung konstant 0) und auf den Flächen mit mindestens 2 Henkeln gibt es hyperbolische Metriken (Krümmung konstant -1).
Für solche Flächen hatten wir in TvF 84 mal diskutiert, wie schnell Geodäten auseinanderdriften:
Wenn man sich (in einer Fläche mit konstanter Krümmung k) zwei Geodäten anschaut, die sich zum Zeitpunkt 0 schneiden, dann beträgt ihr Abstand zum Zeitpunkt t:
– C sin(kt) – falls k positiv
– Ct – falls k=0
– C sinh(-kt) – falls k negativ.
(C hängt vom Winkel ab. Siehe TvF 84 für die Herleitung dieser Formeln aus der Jacobi-Gleichung.)
Also:
bei positiver Krümmung bleibt der Abstand beschränkt,
bei flacher Krümmung wächst der Abstand linear,
bei negativer Krümmung wächst der Abstand exponentiell, nämlich näherungsweise wie Ce-kt/2.
Daraus folgt insbesondere, dass es bei nichtpositiver Krümmung keine konjugierten Punkte geben kann: es kann nicht passieren, dass man während einer Homotopie von Geodäten die Endpunkte festlässt. (Auch wenn es natürlich passieren kann, dass man zu irgendeinem Zeitpunkt wieder eine Geodäte bekommt, die durch den selben Endpunkt geht.)
Also: jede Geodäte hat Index 0 (keine konjugierten Punkte).
Damit ist dann nach Morse-Theorie ΩF homotopie-äquivalent zu einem Zellkomplex, der nur aus 0-dimensionalen Zellen besteht.
Mit anderen Worten: jede Zusammenhangskomponente ist kontrahierbar. (Und man kann sich leicht überlegen, dass die Zusammenhangskomponenten von ΩF gerade den Elementen der Fundamentalgruppe π1F entsprechen: fixiere einen Weg von p nach q, der dem neutralen Element von π1F entsprechen soll, die Verknü,pfung seines Inversen mit jedem anderen Weg gibt dann die gewünschte Bijektion.)
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16, Teil 17, Teil 18, Teil 19, Teil 20, Teil 21, Teil 22, Teil 23, Teil 24, Teil 25, Teil 26, Teil 27, Teil 28, Teil 29, Teil 30, Teil 31, Teil 32, Teil 33, Teil 34, Teil 35, Teil 36, Teil 37, Teil 38, Teil 39, Teil 40, Teil 41, Teil 42, Teil 43, Teil 44, Teil 45, Teil 46, Teil 47, Teil 48, Teil 49, Teil 50, Teil 51, Teil 52, Teil 53, Teil 54, Teil 55, Teil 56, Teil 57, Teil 58, Teil 59, Teil 60, Teil 61, Teil 62, Teil 63, Teil 64, Teil 65, Teil 66, Teil 67, Teil 68, Teil 69, Teil 70, Teil 71, Teil 72, Teil 73, Teil 74, Teil 75, Teil 76, Teil 77, Teil 78, Teil 79, Teil 80, Teil 81, Teil 82, Teil 83, Teil 84, Teil 85, Teil 86, Teil 87, Teil 88, Teil 89, Teil 90, Teil 91, Teil 92, Teil 93, Teil 94, Teil 95, Teil 96, Teil 97, Teil 98, Teil 99, Teil 100, Teil 101, Teil 102, Teil 103, Teil 104, Teil 105, Teil 106, Teil 107, Teil 108, Teil 109, Teil 110, Teil 111, Teil 112, Teil 113, Teil 114, Teil 115, Teil 116, Teil 117, Teil 118, Teil 119, Teil 120, Teil 121, Teil 122, Teil 123, Teil 124, Teil 125, Teil 126, Teil 127, Teil 128, Teil 129, Teil 130, Teil 131, Teil 132, Teil 133, Teil 134, Teil 135, Teil 136, Teil 137, Teil 138, Teil 139, Teil 140, Teil 141, Teil 142, Teil 143, Teil 144, Teil 145, Teil 146, Teil 147, Teil 148, Teil 149, Teil 150, Teil 151, Teil 152, Teil 153, Teil 154, Teil 155, Teil 156, Teil 157, Teil 158, Teil 159, Teil 160, Teil 161, Teil 162, Teil 163, Teil 164, Teil 165, Teil 166, Teil 167, Teil 168, Teil 169, Teil 170, Teil 171, Teil 172, Teil 173, Teil 174, Teil 175, Teil 176, Teil 177, Teil 178, Teil 179, Teil 180, Teil 181, Teil 182, Teil 183, Teil 184, Teil 185, Teil 186, Teil 187, Teil 188, Teil 189, Teil 190, Teil 191, Teil 192, Teil 193, Teil 194, Teil 195, Teil 196, Teil 197, Teil 198, Teil 199, Teil 200, Teil 201, Teil 202, Teil 203, Teil 204, Teil 205, Teil 206, Teil 207, Teil 208, Teil 209, Teil 210, Teil 211, Teil 212, Teil 213, Teil 214, Teil 215, Teil 216, Teil 217, Teil 218, Teil 219, Teil 220, Teil 221


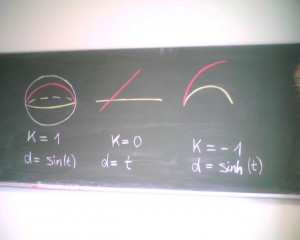
Letzte Kommentare