Vor allem aber würde die Geometrisierungsvermutung bedeuten, dass man 3-Mannigfaltigkeit-Topologie im Wesentlichen auf hyperbolische Geometrie reduzieren könnte. Einerseits wären entsprechend der Vermutung (nach Zerlegung als zusammenhängende Summe und Aufschneiden entlang Tori) alle hinreichend komplizierten 3-Mannigfaltigkeiten hyperbolisch, andererseits ist (für Mannigfaltigkeiten endlichen Volumens) die hyperbolische Metrik eindeutig nach dem Mostowschen Starrheitssatz. Man kann dann also alle topologischen Eigenschaften einer solchen Mannigfaltigkeit aus ihrer hyperbolischen Geometrie ablesen.

Die Gruppe orientierungs-erhaltender Isometrien der hyperbolischen Ebene ist PSL(2,R), für den hyperbolischen Raum ist es PSL(2,C). Uniformisierung gibt für die Fundamentalgruppe einer Fläche zahlreiche Darstellungen nach PSL(2,R). Analog entsprechen die hyperbolischen 3-Mannigfaltigkeiten H3/Γ den diskreten Untergruppen Γ von PSL(2,C), den sogenannten Kleinschen Gruppen. Kleinsche Gruppen waren in den 60er Jahren ein aktives Forschungsthema etwa in den Arbeiten von Ahlfors, Bers und Maskit, allerdings ging es dort meist um Gruppen, für die die Limesmenge wie im Bild oben nicht die gesamte Sphäre ist und für die dann H3/Γ unendliches Volumen hat. Endliches Volumen hat eine hyperbolische 3-Mannigfaltigkeit nur, wenn sie kompakt ist oder wenn der Rand ihrer Kompaktifizierung aus inkompressiblen Tori besteht. In diesem Fall ist die Limesmenge dann die gesamte Sphäre.
Robert Riley beschäftigte sich in den 70er Jahren mit Darstellungen von Knotengruppen in PSL(2,C). Für die Gruppe des Achterknotens fand er 1974 eine treue Darstellung mit diskretem Bild, damit also eine hyperbolische Struktur auf dem Achterknotenkomplement. Er zeigte dann, dass sein Ansatz auch für andere Knoten funktioniert. Seine Arbeit war eines der ersten Beispiele für extensiven Computereinsatz in der reinen Mathematik – zu einer Zeit, als Computer noch mit Lochkarten arbeiteten.
Thurston hörte von dieser Entdeckung erst 1976, als er bereits seit einem Jahr an der Hyperbolisierung von Haken-Mannigfaltigkeiten (irreduziblen, atoroidalen 3-Mannigfaltigkeiten mit inkompressiblen Flächen) arbeitete. (Dazu zählen Knotenkomplemente, weil die in den Knoten eingespannte Seifert-Fläche inkompressibel ist, und allgemeiner überhaupt alle 3-Mannigfaltigkeiten mit nicht-sphärischem Rand.)
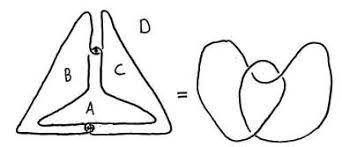
Das Achterknotenbündel ist ein Flächenbündel über dem Kreis, die Faser ist ein punktierter Torus, und die Monodromie die aus der Theorie dynamischer Systeme bekannte Anosovsche Katzenabbildung. Wenn ein solches Flächenbündel hyperbolisch ist, muß die Limesmenge der Fundamentalgruppe der Faser mit der gesamten Limesmenge der hyperbolischen 3-Mannigfaltigkeit, also mit der gesamten Sphäre im Unendlichen übereinstimmen müßte, woraus man – wie er später mit Cannon auch formal bewies – eine surjektive, stetige Abbildung S1—>S2 bekommen würde, also eine Peano-Kurve mit sehr ungewöhnlichen Symmetrien. Das sah zunächst ziemlich unwahrscheinlich aus, aber es gab diese hyperbolische Struktur auf dem Achterknoten nun einmal und die Korrektheit von Rileys Konstruktion war leicht zu überprüfen. Thurston erfuhr später, dass auch Troels Jørgensen in einer unveröffentlichten Arbeit eben diese Faserung zur Konstruktion einer hyperbolischen Metrik auf dem Achterknotenkomplement verwendet hatte. Thurston fand dann noch eine dritte Konstruktion: er zeigte, dass sich das Achterknotenkomplement in zwei ideale Tetraeder zerlegen läßt, die man sich als ideale Tetraeder im hyperbolischen Raum denken kann, so dass die Verklebeabbildungen sich als hyperbolische Isometrien realisieren lassen. Dieser Beweis war zunächst natürlich komplizierter als die von Riley gefundenen expliziten Matrizen, aber er hatte bessere Chancen, sich zu einem allgemeinen Algorithmus zur Bestimmung hyperbolischer Strukturen auf (ideal triangulierten) 3-Manngfaltigkeiten ausbauen zu lassen.
Als allgemeinere Klasse geschlossener 3-Mannigfaltigkeiten betrachtete Thurston dann die geschlossenen 3-Mannigfaltigkeiten, die man durch Chirurgie am Achterknoten erhält, also durch Ankleben eines Volltorus an den Torusrand des Knotenkomplements. Für das Ankleben hat man soviele Möglichkeiten, wie es Diffeomorphismen des Torus gibt, also bis auf Homotopie gerade die Matrizen aus SL(2,Z). Er bewies, dass die so erhaltenen Mannigfaltigkeiten einerseits fast alle hyperbolisch (und die zehn Ausnahmen ebenfalls geometrisierbar) sind, andererseits aber fast alle (bis auf acht) keine inkompressiblen Flächen enthalten, also keine Haken-Mannigfaltigkeit sind. Insbesondere war das ein überzeugendes Gegenbeispiel zu der unter niedrigdimensionalen Topologen kursierenden Frage, ob jede 3-Mannigfaltigkeit entweder eine Seifert-Faserung oder eine Haken-Mannigfaltigkeit ist.
Sein Beweis, dass fast alle durch Chirurgie konstruierten geschlossenen Mannigfaltigkeiten hyperbolisch sind, funktionierte auch für alle anderen Komplemente von Knoten und Verschlingungen, wenn man davon ausgeht, dass das Komplement bereits hyperbolisch ist – was aber gemäß seiner Vermutung für alle Knotenkomplemente mit Ausnahme von Torusknoten und Satellitenknoten der Fall sein sollte. Der Beweis verwendet, dass die komplexe Dimension der Charaktervarietät einer Verschlingung die Anzahl der Komponenten der Verschlingung ist. (Im Fall eines Knotens also 1.) Parametrisiert wird sie durch die Spuren der Bilder der Meridiane und diese Parametrisierung ist holomorph, insbesondere wird eine offene Menge von Parametern angenommen. Für die vollständige hyperbolische Metrik auf dem Knotenkomplement sind die Monodromien der Meridiane eine parabolische Isometrie der Spur 2. Hingegen entsprechen hyperbolische Metriken auf der durch Chirurgie erhaltenen Mannigfaltigkeit unvollständigen hyperbolischen Metriken auf dem Knotenkomplement, bei denen die Monodromie der Meridiane eine elliptische Isometrie ist, deren Spur für große p,q gegen 2 geht. Nach Mostows Starrheitssatz gibt es nur eine vollständige hyperbolische Metrik auf dem Knotenkomplement. Es gibt also genau eine Darstellung mit Parameter (2,2,…,2), woraus sich mit der Holomorphie der Parametrisierung herleiten läßt, dass alle nahegelegenen Spur-Parameter genau einmal realisiert werden müssen. Insbesondere gibt es für hinreichend große p,q Parameter, welche die q/p-Dehn-Chirurgie realisieren.


Kommentare (9)