Eine (komplexe) ebene Kurve kann man auf zwei Arten beschreiben: implizit durch eine Gleichung F(x,y)=0 oder explizit als Bild einer parametrisierten Kurve c:C–>C2. Kegelschnitte und auch singuläre Kubiken lassen sich durch rationale Funktionen parametrisieren, nichtsinguläre Kubiken (elliptische Kurven) aber nicht: für ihre Parametrisierung benötigt man die unten abgebildete Weierstraßsche ℘-Funktion eines Gitters L. Die elliptische Kurve ist (nach Hinzunahme des Punktes im Unendlichen) äquivalent zu einem Torus C/L für ein Gitter L, und die Parametrisierung der Kurve im C2 erfolgt dann durch (℘,℘’).

Das Problem, beliebige komplexe algebraische Kurven zu parametrisieren, wurde im 19. Jahrhundert als Uniformisierungsproblem bezeichnet. Felix Klein hatte 1878 entdeckt, dass die Quartik x3y+y3z+z3x=0 (in homogenen Koordinaten der projektiven Ebene) als Kompaktifizierung eines Quotienten H/Γ der hyperbolischen Ebene H parametrisiert werden kann: die Gruppe Γ ist eine Untergruppe der durch gebrochen-lineare Transformationen auf H wirkenden Matrixgruppe SL(2,R), nämlich die Hauptkongruenzgruppe zum Ideal (2cos(2π/7)-2), einem der Primfaktoren von (7). Das Bild zeigt einen Fundamentalbereich in der hyperbolischen Ebene, Kanten mit gleichen Ziffern werden identifiziert; der Quotient ist eine Fläche vom Geschlecht 3.

Solche Parametrisierungen galten zunächst als exotische Beispiele. 1880 hatte Henri Poincaré dann den Einfall, dass die Monodromien gewisser Differentialgleichungen gerade Isometrien der hyperbolischen Ebene sind, die Lösungen der Differentialgleichungen also wie Kleins Quartik als H/Γ für gewisse Monodromiegruppen Γ parametrisiert werden können. Felix Klein vermutete darauf, dass man mit Poincarés Konstruktion die Uniformisierung aller komplexen Kurven erhalten könne. Er bezeichnete das als Grenzkreistheorem, weil die Uniformisierung die universelle Überlagerung mit einem Grenkreis ausstattet. Beweisen wollte er das durch die Identifizierung der 6g-6 Moduli algebraischer Kurven vom Geschlecht g mit der Anzahl der Parameter der möglichen Fundamentalpolygone für diskrete Isometriegruppen der hyperbolischen Ebene. Sein Beweis war fehlerhaft, er diente aber immerhin Hermann Schwarz als Anlaß für die Entwicklung der Überlagerungstheorie, mit der das Problem auf den Beweis des (damals ebenfalls noch nicht bewiesenen) Abbildungssatzes zurückgeführt werden kann. Poincaré bewies dann mittels eines “Stetigkeitsarguments”, dass jede algebraische Kurve uniformisierbar ist und dass jede lineare Differentialgleichung mit algebraischen Koeffizienten durch Fuchssche Funktionen integriert werden kann. (Das Stetigkeitsargument besagt, dass injektive, stetige Abbildungen zwischen Mannigfaltigkeiten derselben Dimension surjektiv sein müssen. Das wurde später von Brouwer bewiesen.)

Aus dem Uniformisierungssatz folgt, dass jede Fläche geometrisiert werden kann: die Sphäre durch ihre runde Metrik, der Torus durch eine flache Metrik, die Flächen höheren Geschlechts durch hyperbolische Metriken. Niemand vermutete, dass es eine solche Uniformisierung auch für 3-Mannigfaltigkeiten geben könnte, erst Thurston brachte in den 70er Jahren diese Idee auf.
Thurston litt unter Strabismus, er hatte von Geburt an Schwierigkeiten mit dem dreidimensionalen Sehen. Als Kleinkind hatte seine Mutter mit ihm immer wieder bunte Muster angeschaut und er hatte ein ungewöhnliches Vorstellungsvermögen für dreidimensionale Geometrie entwickelt. In Vorträgen stand er manchmal einfach auf und malte komplizierte Bilder an die Tafel, mit denen er ein Beispiel oder Gegenbeispiel für eine mathematische Behauptung illustrieren wollte.
Schon während seiner Doktorarbeit über Blätterungen hatte er darüber nachgedacht, ob es eine Geometrisierung wie für Flächen auch im Dreidimensionalen geben könnte. Bekannt wurde er dann aber zunächst mit seinen Arbeiten über Blätterungen; er bewies 1974, dass jede Mannigfaltigkeit der Euler-Charakteristik Null eine Blätterung der Kodimension 1 besitzt.
Über die Jahre hatte er eine gewisse Intuition für hyperbolische 3-Mannigfaltigkeiten aufgebaut und schließlich vermutete oder spekulierte er, dass jede irreduzible 3-Mannigfaltigkeit ohne eingebettete inkompressible Tori eine von acht geometrischen Strukturen haben könnte, wobei die hyperbolischen Strukturen die häufigsten sein sollten, nämlich die auf irreduziblen, atoroidalen (d.h. ohne immersierte inkompressible Tori) 3-Mannigfaltigkeiten. Zu dieser Zeit bewiesen Waldhausens Student Johannson sowie unabhängig davon Jaco und Shalen gerade, dass man irreduzible 3-Mannigfaltigkeiten entlang Tori in Stücke schneiden kann (und die Stücke entweder atoroidal oder Seifert-Faserungen sind). Außerdem war schon länger bekannt, dass man jede 3-Mannigfaltigkeit als zusammenhängende Summe irreduzibler (oder S1xS2)-Stücke zerlegen kann. Damit behauptete seine Vermutung, dass man jede 3-Mannigfaltigkeit in geometrisierbare Stücke zerlegen kann.
Die Geometrisierungsvermutung subsumierte viele ältere Vermutungen, wie die berühmte Poincaré-Vermutung über einfach zusammenhängende 3-Mannigfaltigkeiten (diese sollen homöomorph zur S3 sein), allgemeiner das sphärische Raumformproblem (eine von Hopf aufgestellte Vermutung über endliche Gruppenwirkungen auf S3, die konjugiert zu einer Untergruppe von SO(4) sein sollen), die Smith-Vermutung (Fixpunktmengen von Diffeomorphismen der S3 sind unverknotet), die Endlichkeit der Abbildungsklassengruppe, die Frage nach der residuellen Endlichkeit der Fundamentalgruppen von 3-Mannigfaltigkeiten, oder die Frage nach der Klassifikation der möglichen universellen Überlagerungen von 3-Mannigfaltigkeiten.
Vor allem aber würde die Geometrisierungsvermutung bedeuten, dass man 3-Mannigfaltigkeit-Topologie im Wesentlichen auf hyperbolische Geometrie reduzieren könnte. Einerseits wären entsprechend der Vermutung (nach Zerlegung als zusammenhängende Summe und Aufschneiden entlang Tori) alle hinreichend komplizierten 3-Mannigfaltigkeiten hyperbolisch, andererseits ist (für Mannigfaltigkeiten endlichen Volumens) die hyperbolische Metrik eindeutig nach dem Mostowschen Starrheitssatz. Man kann dann also alle topologischen Eigenschaften einer solchen Mannigfaltigkeit aus ihrer hyperbolischen Geometrie ablesen.

Die Gruppe orientierungs-erhaltender Isometrien der hyperbolischen Ebene ist PSL(2,R), für den hyperbolischen Raum ist es PSL(2,C). Uniformisierung gibt für die Fundamentalgruppe einer Fläche zahlreiche Darstellungen nach PSL(2,R). Analog entsprechen die hyperbolischen 3-Mannigfaltigkeiten H3/Γ den diskreten Untergruppen Γ von PSL(2,C), den sogenannten Kleinschen Gruppen. Kleinsche Gruppen waren in den 60er Jahren ein aktives Forschungsthema etwa in den Arbeiten von Ahlfors, Bers und Maskit, allerdings ging es dort meist um Gruppen, für die die Limesmenge wie im Bild oben nicht die gesamte Sphäre ist und für die dann H3/Γ unendliches Volumen hat. Endliches Volumen hat eine hyperbolische 3-Mannigfaltigkeit nur, wenn sie kompakt ist oder wenn der Rand ihrer Kompaktifizierung aus inkompressiblen Tori besteht. In diesem Fall ist die Limesmenge dann die gesamte Sphäre.
Robert Riley beschäftigte sich in den 70er Jahren mit Darstellungen von Knotengruppen in PSL(2,C). Für die Gruppe des Achterknotens fand er 1974 eine treue Darstellung mit diskretem Bild, damit also eine hyperbolische Struktur auf dem Achterknotenkomplement. Er zeigte dann, dass sein Ansatz auch für andere Knoten funktioniert. Seine Arbeit war eines der ersten Beispiele für extensiven Computereinsatz in der reinen Mathematik – zu einer Zeit, als Computer noch mit Lochkarten arbeiteten.
Thurston hörte von dieser Entdeckung erst 1976, als er bereits seit einem Jahr an der Hyperbolisierung von Haken-Mannigfaltigkeiten (irreduziblen, atoroidalen 3-Mannigfaltigkeiten mit inkompressiblen Flächen) arbeitete. (Dazu zählen Knotenkomplemente, weil die in den Knoten eingespannte Seifert-Fläche inkompressibel ist, und allgemeiner überhaupt alle 3-Mannigfaltigkeiten mit nicht-sphärischem Rand.)
Das Achterknotenbündel ist ein Flächenbündel über dem Kreis, die Faser ist ein punktierter Torus, und die Monodromie die aus der Theorie dynamischer Systeme bekannte Anosovsche Katzenabbildung. Wenn ein solches Flächenbündel hyperbolisch ist, muß die Limesmenge der Fundamentalgruppe der Faser mit der gesamten Limesmenge der hyperbolischen 3-Mannigfaltigkeit, also mit der gesamten Sphäre im Unendlichen übereinstimmen müßte, woraus man – wie er später mit Cannon auch formal bewies – eine surjektive, stetige Abbildung S1—>S2 bekommen würde, also eine Peano-Kurve mit sehr ungewöhnlichen Symmetrien. Das sah zunächst ziemlich unwahrscheinlich aus, aber es gab diese hyperbolische Struktur auf dem Achterknoten nun einmal und die Korrektheit von Rileys Konstruktion war leicht zu überprüfen. Thurston erfuhr später, dass auch Troels Jørgensen in einer unveröffentlichten Arbeit eben diese Faserung zur Konstruktion einer hyperbolischen Metrik auf dem Achterknotenkomplement verwendet hatte. Thurston fand dann noch eine dritte Konstruktion: er zeigte, dass sich das Achterknotenkomplement in zwei ideale Tetraeder zerlegen läßt, die man sich als ideale Tetraeder im hyperbolischen Raum denken kann, so dass die Verklebeabbildungen sich als hyperbolische Isometrien realisieren lassen. Dieser Beweis war zunächst natürlich komplizierter als die von Riley gefundenen expliziten Matrizen, aber er hatte bessere Chancen, sich zu einem allgemeinen Algorithmus zur Bestimmung hyperbolischer Strukturen auf (ideal triangulierten) 3-Manngfaltigkeiten ausbauen zu lassen.
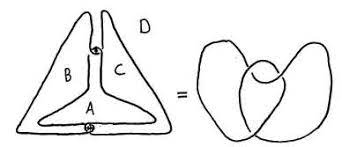
Als allgemeinere Klasse geschlossener 3-Mannigfaltigkeiten betrachtete Thurston dann die geschlossenen 3-Mannigfaltigkeiten, die man durch Chirurgie am Achterknoten erhält, also durch Ankleben eines Volltorus an den Torusrand des Knotenkomplements. Für das Ankleben hat man soviele Möglichkeiten, wie es Diffeomorphismen des Torus gibt, also bis auf Homotopie gerade die Matrizen aus SL(2,Z). Er bewies, dass die so erhaltenen Mannigfaltigkeiten einerseits fast alle hyperbolisch (und die zehn Ausnahmen ebenfalls geometrisierbar) sind, andererseits aber fast alle (bis auf acht) keine inkompressiblen Flächen enthalten, also keine Haken-Mannigfaltigkeit sind. Insbesondere war das ein überzeugendes Gegenbeispiel zu der unter niedrigdimensionalen Topologen kursierenden Frage, ob jede 3-Mannigfaltigkeit entweder eine Seifert-Faserung oder eine Haken-Mannigfaltigkeit ist.
Sein Beweis, dass fast alle durch Chirurgie konstruierten geschlossenen Mannigfaltigkeiten hyperbolisch sind, funktionierte auch für alle anderen Komplemente von Knoten und Verschlingungen, wenn man davon ausgeht, dass das Komplement bereits hyperbolisch ist – was aber gemäß seiner Vermutung für alle Knotenkomplemente mit Ausnahme von Torusknoten und Satellitenknoten der Fall sein sollte. Der Beweis verwendet, dass die komplexe Dimension der Charaktervarietät einer Verschlingung die Anzahl der Komponenten der Verschlingung ist. (Im Fall eines Knotens also 1.) Parametrisiert wird sie durch die Spuren der Bilder der Meridiane und diese Parametrisierung ist holomorph, insbesondere wird eine offene Menge von Parametern angenommen. Für die vollständige hyperbolische Metrik auf dem Knotenkomplement sind die Monodromien der Meridiane eine parabolische Isometrie der Spur 2. Hingegen entsprechen hyperbolische Metriken auf der durch Chirurgie erhaltenen Mannigfaltigkeit unvollständigen hyperbolischen Metriken auf dem Knotenkomplement, bei denen die Monodromie der Meridiane eine elliptische Isometrie ist, deren Spur für große p,q gegen 2 geht. Nach Mostows Starrheitssatz gibt es nur eine vollständige hyperbolische Metrik auf dem Knotenkomplement. Es gibt also genau eine Darstellung mit Parameter (2,2,…,2), woraus sich mit der Holomorphie der Parametrisierung herleiten läßt, dass alle nahegelegenen Spur-Parameter genau einmal realisiert werden müssen. Insbesondere gibt es für hinreichend große p,q Parameter, welche die q/p-Dehn-Chirurgie realisieren.
Nach einem 1961 von Lickorish bewiesenen Satz lassen sich alle 3-Mannigfaltigkeiten durch Dehn-Chirurgien an Verschlingungen in der 3-Sphäre realisieren. Mit seinem Satz über die Hyperbolizität fast aller Dehn-Chirurgien hatte Thurston also eine starke Evidenz für die Richtigkeit der Geometrisierungsvermutung. In den folgenden Jahren erarbeitete er einen Beweis der Geometrisierungsvermutung für Haken-Mannigfaltigkeiten, der Ideen aus Topologie, hyperbolischer Geometrie, komplexer Analysis, Dynamik und Ergodentheorie verwendete. Die Idee ist, dass man Haken-Mannigfaltigkeiten durch Aufschneiden entlang Flächen vereinfachen und so Induktionsbeweise führen kann. In diesem Fall besteht der Induktionsschritt darin, eine hyperbolische Metrik auf der aufgeschnittenen Mannigfaltigkeit so zu deformieren, dass sie in gewisser Weise auf den beiden Randkomponenten (genauer deren Entsprechung im Rand im Unendlichen) übereinstimmt und man dann eine hyperbolische Metrik auf der verklebten Mannigfaltigkeit bekommt. Dafür muß man letztlich einen Fixpunktsatz auf dem Teichmüller-Raum der Fläche beweisen. Thurstons Beweis sollte in einer aus sieben Teilen bestehenden Arbeit erscheinen, Teil I wurde 1986 in den Annals of Mathematics veröffentlicht, Teil II und III erschienen immerhin noch als Preprint. Einen Beweis des Fixpunktsatzes auf dem Teichmüller-Raum (und damit letztlich von Thurstons Vermutung für Haken-Mannigfaltigkeiten) veröffentlichte 1990 Curtis McMullen.
Bild: https://mathshistory.st-andrews.ac.uk/Biographies/Thurston/pictdisplay/


Kommentare (9)