Theorema Magnum MXM: die Witten-Vermutung

Atiyah tat viel für die Verbreitung der neuen physikalischen Ansätze unter den Mathematikern. Er entwickelte insbesondere eine Axiomatik topologischer Quantenfeldtheorien, nachdem Witten zuvor gezeigt hatte, dass sowohl Donaldsons Arbeit über Instantonen auf 4-Mannigfaltigkeiten als auch Floers neue Homologietheorie sich in diesem Sinne interpretieren lassen. Atiyahs Ansatz ging davon aus, dass jeder Mannigfaltigkeit ein Modul (in der Regel ein Hilbert-Raum) und jedem Bordismus ein Element des dem Rand zugeordneten Moduls (der “Vakuumzustand”) zugeordnet wird, so dass fünf Axiome gelten sollen.

Eine weitere überraschende Anwendung physikalischer Analogien wurde eine von Witten vermutete Formel für die Berechnung von Schnittzahlen auf dem Modulraum Riemannscher Flächen.
Bernhard Riemann hat die später nach ihm benannten Riemannschen Flächen 1851 als verzweigte Überlagerungen eingeführt und topologisch (durch Zählen der Verzweigungspunkte) argumentiert, dass es 3g-3 komplexe Moduli für Riemannsche Flächen vom Geschlecht g≥2 gibt. Man findet in seiner Arbeit keine präzise Definition der Moduli. Oswald Teichmüller fand 1939 einen Satz über die Existenz und Eindeutigkeit extremaler quasikonformer Abbildungen, mit dessen Hilfe er die Dimension des Modulraums bestimmen konnte, vollständige Beweise wurden später von Ahlfors und Bers ausgearbeitet. Der Modulraum ist der Quotient des zu C^3g-3 holomorphen Teichmüller-Raums unter der Wirkung der Abbildungsklassengruppe. Die Wirkung der Abbildungsklassengruppe auf dem Teichmüller-Raum ist eigentlich diskontinuierlich, aber nicht frei, weshalb es sich beim Modulraum um eine Orbifaltigkeit handelt.
Aus Sicht der algebraischen Geometrie handelt es sich bei Riemannschen Flächen um glatte projektive Kurven. Mit den von Grothendieck eingeführten Methoden konnte man Teichmüller-Räume als Schemata betrachten, es war aber zunächst nicht klar, ob sie eine quasi-projektive Varietät sind. Das bewiesen dann Mumford und Bailey mit Methoden der von Mumford entwickelten geometrischen Invariantentheorie und damit wurde auch der Modulraum eine quasi-projektive Varietät, der sogenannte Modulstack.
Man kann diesen Modulstack kompaktifizieren, indem man zu den glatten Kurven noch diejenigen hinzunimmt, die nur (lokal wie xy=0 aussehende) Doppelpunkte als Singularitäten und endliche Automorphismengruppen haben. Deligne und Mumford bewiesen, dass diese Kompaktifizierung eine irreduzible Varietät ist. Auch für den Modulstack der Kurven vom Geschlecht g mit n markierten Punkten konnten sie so eine irreduzible Varietät als Kompaktifizierung konstruieren. Auf diesem kompakten Raum kann man nun Schnitttheorie betreiben, d.h. man kann Schnittzahlen von Kohomologieklassen definieren, wenn deren Dimensionen sich zu aufaddieren. Die sehr viel später von Madsen und Weiss bewiesene Mumford-Vermutung beschreibt zumindest die stabile Kohomologie des stabilen Modulraums als von den Morita-Miller-Mumford-Klassen (MMM-Klassen) erzeugt. Für die Schnittzahlen dieser Kohomologieklassen hatte man aber keine plausible Vermutung.
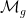
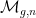
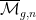
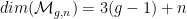
Eng mit den MMM-Klassen zusammen hängen Kohomologieklassen τ_i, die man als erste Chern-Klassen gewisser Linienbündel erhält: Zu jedem der n markierten Punkte x_i hat man ein Linienbündel L_i über der Kurve, dessen Faser über einem Punkt des Modulraums gerade die Faser des holomorphen Kotangentialbündels der Fläche in x_i für die dem Punkt des Modulraums entsprechende komplexe Struktur ist. Witten zeigte, dass die Schnitttheorie der τ_i=c₁(L_i) dieselbe Information liefert wie die Schnittheorie der MMM-Klassen.
Für natürliche Zahlen mit d1+…+dk=dim(Mg,n)=3(g-1)+n kann man das Produkt auf der Fundamentalklasse der Deligne-Mumford-Kompaktifizierung auswerten. Das kann man interpretieren als die Schnittzahlen der zu den Linienbündeln dualen Untermannigfaltigkeiten. Diese Schnittzahlen organisiert man mittels einer erzeugenden formalen Potenzreihe F.