Die Stringtheorie entstand ursprünglich aus dem Versuch der Physiker, die starke Wechselwirkung zu verstehen. Bei ihrer Entwicklung kamen reichhaltige mathematische Strukturen zutage, die aber wenig mit starker Wechselwirkung zu tun hatten. In den 70er Jahren war dann mit einer nichtabelschen Eichtheorie – der Beschreibung durch ein Yang-Mills-Feld zur Eichgruppe SU(3)xSU(2)xU(1) – eine erfolgreiche Theorie zur Erklärung der starken Wechselwirkung entstanden, das sogenannte Standardmodell. Doch die mathematische Struktur der Stringtheorie behielt ihre Faszination und während die ursprüngliche Motivation verblaßte, glaubte man nun, dass Stringtheorie den Rahmen für die Versöhnung von Gravitation und Quantenmechanik liefern könnte. Dafür muß man glauben, dass es zehn statt vier Dimensionen gibt, also neben der 4-dimensionalen Raum-Zeit noch sechs weitere Dimensionen in einer Größenordnung von 10-35 Metern. Diese zusätzlichen Dimensionen sollen eine Calabi-Yau-Mannigfaltigkeit bilden, also eine komplexe 3-Faltigkeit komplizierter Topologie, die die Voraussetzungen der von Yau bewiesenen Calabi-Vermutung erfüllt.

Wesentliche Beiträge zur Stringtheorie kamen von Edward Witten, der, obwohl er ein Physiker war, die Mathematik wie nur wenige Mathematiker beherrschte und immer wieder überraschende mathematische Interpretationen physikalischer Ideen fand.
Anfang der 80er Jahre fand er mit Hilfe des Dirac-Operators einen einfacheren Beweis der von Schoen und Yau bewiesenen Positivität der Energie in der Gravitationstheorie. Danach bewies er mit Vafa, einem iranischen Physiker, physikalisch motivierte Abschätzungen für die Eigenwerte des Dirac-Operators. Seit Ende der 80er Jahre befaßte er sich mit einer hypothetischen Verallgemeinerung des Dirac-Operators auf Schleifenräumen von Mannifaltigkeiten: der Index dieses Operators sollte ein gewisses elliptisches Geschlecht sein. Darüber hinaus hatten seine Arbeiten über globale Anomalien die Eta-Invariante prominent gemacht. Eine von ihm physikalisch begründete Formel konnten Atiyah und Singer aus allgemeinen Prinzipien herleiten. Wegen analytischer Schwierigkeiten verzögerte sich die Arbeit, die sie dann mit Donnolly doch noch abschloßen und in den Annals of Mathematics veröffentlichten, einen unabhängigen Beweis gab Werner Müller.
Vor allem beeindruckte Witten die Mathematiker aber mit einer physikalischen Interpretation des wenige Jahre zuvor von Vaughan Jones gefundenen Knotenpolynoms.
Witten fand für das Jones-Polynom eine stringtheoretische Interpretation mit Hilfe eines Pfadintegrals.
Für einen Zusammenhang A auf einem (trivialen) G-Bündel über einer 3-Mannigfaltigkeit M, der als 1-Form mit Werten in der Lie-Algebra von G angesehen werden kann, betrachtet man das Chern-Simons-Funktional
Eine Knoteninvariante erhält man, indem man die Holonomie des Knotens (bezüglich des Zusammenhangs) ins Spiel bringt und darauf noch eine Darstellung ρ von G anwendet. Für M=R3 und G=SU(2) sowie ρ die Standard-Darstellung von SU(2) bekommt man das Jones-Polynom. Dieses wird also als Pfadintegral für eine 3-dimensionale Eichtheorie interpretiert und man kann das Polynom jetzt für Knoten in beliebigen 3-Mannigfaltigkeiten definieren. (Insbesondere für den leeren Knoten, womit man eine 3-Mannigfaltigkeitsinvariante bekommt.) Obwohl das Integral nur ein heuristisches Werkzeug ist, führt es in diesem Fall zu einem rigorosen Ansatz im Sinne der klassischen Mechanik. Reshetikhin und Turaev nutzten die Formeln für eine rigorose algorithmische Definition. Daraus entwickelte sich eine ganze Industrie von Quanteninvarianten.
Der neue Zugang zu Knoteninvarianten und der neue Beweis der Positivität der Energie waren dann auch die ersten Punkte in Atiyahs Laudatio für die Fields-Medaille, die Witten – als erster Physiker – auf dem ICM in Kyoto erhielt.
Bernhard Riemann hat die später nach ihm benannten Riemannschen Flächen 1851 als verzweigte Überlagerungen eingeführt und topologisch (durch Zählen der Verzweigungspunkte) argumentiert, dass es 3g-3 komplexe Moduli für Riemannsche Flächen vom Geschlecht g≥2 gibt. Man findet in seiner Arbeit keine präzise Definition der Moduli. Oswald Teichmüller fand 1939 einen Satz über die Existenz und Eindeutigkeit extremaler quasikonformer Abbildungen, mit dessen Hilfe er die Dimension des Modulraums bestimmen konnte, vollständige Beweise wurden später von Ahlfors und Bers ausgearbeitet. Der Modulraum ist der Quotient des zu C3g-3 holomorphen Teichmüller-Raums unter der Wirkung der Abbildungsklassengruppe. Die Wirkung der Abbildungsklassengruppe auf dem Teichmüller-Raum ist eigentlich diskontinuierlich, aber nicht frei, weshalb es sich beim Modulraum um eine Orbifaltigkeit handelt.
Aus Sicht der algebraischen Geometrie handelt es sich bei Riemannschen Flächen um glatte projektive Kurven. Mit den von Grothendieck eingeführten Methoden konnte man Teichmüller-Räume als Schemata betrachten, es war aber zunächst nicht klar, ob sie eine quasi-projektive Varietät sind. Das bewiesen dann Mumford und Bailey mit Methoden der von Mumford entwickelten geometrischen Invariantentheorie und damit wurde auch der Modulraum eine quasi-projektive Varietät, der sogenannte Modulstack.
Man kann diesen Modulstack
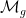

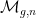
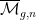
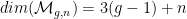
Eng mit den MMM-Klassen zusammen hängen Kohomologieklassen τi, die man als erste Chern-Klassen gewisser Linienbündel erhält: Zu jedem der n markierten Punkte xi hat man ein Linienbündel Li über der Kurve, dessen Faser über einem Punkt des Modulraums gerade die Faser des holomorphen Kotangentialbündels der Fläche in xi für die dem Punkt des Modulraums entsprechende komplexe Struktur ist. Witten zeigte, dass die Schnitttheorie der τi=c1(Li) dieselbe Information liefert wie die Schnittheorie der MMM-Klassen.
Für natürliche Zahlen mit d1+…+dk=dim(Mg,n)=3(g-1)+n kann man das Produkt

Diese Schnittzahlen und ihre erzeugende Potenzreihe
Die klassische Korteweg-de-Vries–Gleichung war im 19. Jahrhundert zur Analyse von Flachwasserwellen in engen Kanälen vorgeschlagen worden. Sie beschreibt sogenannte Solitonen, das sind Wellenpakete, die sich ohne Änderung ihrer Form durch ein dispersives, nichtlineares Medium bewegen, zum Beispiel Flachwasserwellen in engen Kanälen. Ihre Anwendbarkeit für echte Wasserwellen in Kanälen benötigt einige Annahmen. Für die Mathematik ist sie aber interessant, weil sie besser verstanden ist als die meisten anderen nichtlinearen Differentialgleichungen. Sie ist ein vollständig integrables System und war 1967 mit der von Gardner, Greene, Kruskal und Miura für diesen Zweck entwickelten inversen Streutheorie exakt gelöst worden. Peter Lax fand eine operatortheoretische Formulierung ihrer Methode, woraus sich dann eine allgemeine Theorie von Solitonen entwickelte.
Er vertiefte sich so in das Problem, dass er nicht zum abendlichen Empfang ging. Zwei Tage später auf der traditionellen Bootsfahrt erklärte er Atiyah, wie er das Problem lösen wolle. Der war so angetan, dass er ihm bei Hirzebruch eine Einladung an das Bonner Max-Planck-Institut für ein ganzes Jahr besorgte. Kontsevich schrieb sich dann als Doktorand von Zagier an der Bonner Universität ein und verfaßte über den Beweis der Witten-Vermutung seine Doktorarbeit.
Es ist schwer vorstellbar, dass ein Mathematiker ohne physikalischen Hintergrund auf die Idee gekommen wäre, dass die KdV-Gleichung eine Rolle bei der Berechnung von Schnittzahlen spielt. Kontsevichs Beweis verwendete jedoch nicht den ursprünglichen physikalischen Ansatz, sondern sein kombinatorisches Modell des Modulraums, um F durch Matrixintegrale auszudrücken und dann kombinatorisch Eigenschaften des Matrixintegrals zu zeigen, aus denen die gewünschte Differentialgleichung folgt.
Kommentare (3)