“If you loose your key in hyperbolic space, you never find it back.”
Auseinanderdriften von Geodäten, Jacobi-Gleichung und Brownsche Bewegung.
Krümmung ist, wie wir in TvF 48ff. mal geschrieben hatten, durch Formeln definiert, deren anschauliche Bedeutung nicht unmittelbar einleuchtet.
Vorletzte Woche hatten wir darüber geschrieben, daß kleinere (d.h. “negativere”) Krümmung anschaulich bedeutet, daß Dreiecke “dünner” werden.
Letztlich liegt das daran, daß bei negativerer Krümmung Geodäten schneller auseinanderdriften.
Wenn man sich (in einer Fläche mit konstanter Krümmung k) zwei Geodäten anschaut, die sich zum Zeitpunkt 0 schneiden, dann beträgt ihr Abstand zum Zeitpunkt t:
– C sin(kt) – – falls k positiv
– Ct – – falls k=0
– C sinh(-kt) – – falls k negativ.
(C hängt vom Winkel ab. Siehe den letzten Absatz unten für die Herleitung dieser Formeln aus der Jacobi-Gleichung.)
Also:
bei positiver Krümmung bleibt der Abstand beschränkt,
bei flacher Krümmung wächst der Abstand linear,
bei negativer Krümmung wächst der Abstand exponentiell, nämlich näherungsweise wie Ce-kt/2.
Es ist sicher anschaulich klar, daß bei exponentiell auseinanderdriftenden Geodäten dann auch das Volumen von Kugeln in negativ gekrümmten Räumen exponentiell mit dem Radius wachsen sollte. Dazu nächste Woche.
Brownsche Bewegung
Eine andere Konsequenz ist, daß Irrfahrten (wie die Brownsche Bewegung) nicht zum Ausgangspunkt zurückkehren.
“If you loose your key in hyperbolic space, you never find it back” brachte es mal ein Prof bei einer Sommerschule auf den Punkt.
Mathematisch geht es dabei um folgendes: Eine Irrfahrt ist eine zufällige Bewegung, bei der man jederzeit seine Richtung zufällig wählt (d.h. alle Richtungen sind gleichwahrscheinlich). Kann man dann (mit Wahrscheinlichkeit 1) davon ausgehen, daß man immer wieder zum Ausgangspunkt zurückkehrt?
Diese Frage war 1912 von Polya untersucht worden, siehe https://www.amt.canberra.edu.au/biogpolya.html: “Inspired by walks in the woods near Zurich, Pólya in 1912 published one of his major results, the solution of the random walk problem. In this problem one walks in an infinite rectangular grid system, at each node having an equal probability of walking to each of the adjoining nodes on his next leg. Pólya was able to show that in the two dimensional case it was almost certain (but with probability 1) that one would eventually return to the original position.”
Polya veröffentlichte sein Ergebnis 1921 (auf Deutsch) in den “Mathematische Annalen” unter dem Titel “Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Straßennetz”.
Also: in der euklidischen Ebene (aber nicht im 3-dimensionalen Raum) kommt man mit Wahrscheinlichkeit 1 unendlich oft zu der Stelle zurück, wo man seinen Schlüssel verloren hat. (Man sagt: die Brownsche Bewegung in der Ebene ist “rekurrent”.)
Vorgerechnet wird das z.B. auf Seite 8/9 in de la Harpe’s Buch. Die Rückkehrwahrscheinlichkeit im 3-dimensionalen Raum wird dort mit 0.35 angegeben.
Allgemein ist es so, daß die Rückkehrwahrscheinlichkeit eng mit dem Volumenwachstum zusammenhängt (dazu nächste Woche). Insbesondere ist die Brownsche Bewegung in negativ gekrümmten Räumen nicht-rekurrent (“transient”).
Jacobi-Gleichung
Noch kurz zum mathematischen Hintergrund der auseinanderdriftenden Geodäten.
Das Auseinanderdriften von Geodäten wird durch die Jacobi-Gleichung beschrieben.
Das Setting ist dabei folgendes: man hat eine Menge von Geodäten, die von einem Parameter s abhängen. (Den Zeitparameter der Geodäten nennt man t.)
H(t,s) ist dann die Geodäte mit Parameter s, zum Zeitpunkt t:
Die Ableitung dH/dt ist natürlich die Tangente T an die jeweilige Geodäte.
Die Ableitung dH/ds ist das sogenannte Jacobi-Feld J(t,s). Die Größe des Jacobi-Felds mißt, wie schnell die Geodäten auseinanderdriften.
Die Jacobi-Gleichung sagt:
J”+ R(J,T)T=0
wobei R der Riemannsche Krümmungstensor ist. Bei konstanter Krümmung K vereinfacht sich das zu
J”+KJ=0.
Für K=0 hat J”=0 (wegen J(0)=0) nur lineare Lösungen: J(t)=Ct, die Konstante C ist dabei die Ableitung in 0: C=J'(0).
Für K=1 hat J”+J=0 die Lösungen J(t)=C sin(t).
Für K=-1 hat J”-J=0 die Lösungen J(t)= C sinh(t).
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16, Teil 17, Teil 18, Teil 19, Teil 20, Teil 21, Teil 22, Teil 23, Teil 24, Teil 25, Teil 26, Teil 27, Teil 28, Teil 29, Teil 30, Teil 31, Teil 32, Teil 33, Teil 34, Teil 35, Teil 36, Teil 37, Teil 38, Teil 39, Teil 40, Teil 41, Teil 42, Teil 43, Teil 44, Teil 45, Teil 46, Teil 47, Teil 48, Teil 49, Teil 50, Teil 51, Teil 52, Teil 53, Teil 54, Teil 55, Teil 56, Teil 57, Teil 58, Teil 59, Teil 60, Teil 61, Teil 62, Teil 63, Teil 64, Teil 65, Teil 66, Teil 67, Teil 68, Teil 69, Teil 70, Teil 71, Teil 72, Teil 73, Teil 74, Teil 75, Teil 76, Teil 77, Teil 78, Teil 79, Teil 80, Teil 81, Teil 82, Teil 83

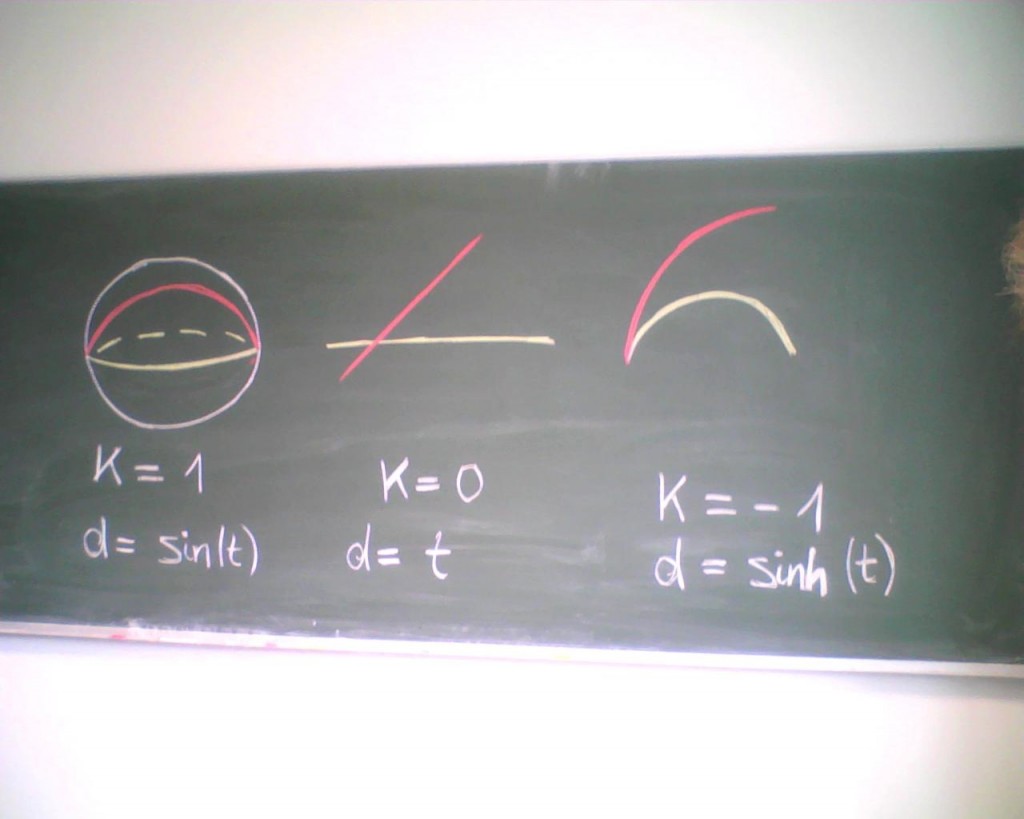
Kommentare (1)