Von Thilo / 26. Juni 2013 / 17 Kommentare

Letzten Endes bekommt man stets bestätigt was man ohnehin schon glaubte – das will uns xkcd wohl mit seiner heutigen Graphik sagen:

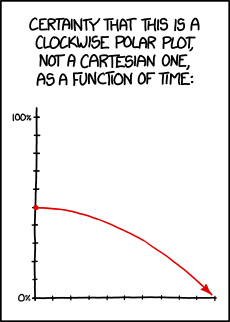
Wenn man glaubt, es handele sich um einen Funktionengraphen in der x-y-Ebene, dann nimmt die Wahrscheinlichkeit (dafür, dass es sich um Polarkoordinaten handelt) von zunächst 50% auf 0% ab, man ist am Ende also sicher, dass es sich um keine Polarkoordinaten handelt, was man ja auch von Anfang an angenommen hatte.

Wenn man hingegen glaubt, es handele sich um Polarkoordinaten, dann muss man konsequenterweise bei φ=0 beginnen und gegen den Uhrzeigersinn laufen. Am Ende hat man also eine Wahrscheinlichkeit von 50% für die Polarkoordinaten, an die man ja sowieso schon geglaubt hatte.

Konsequenter im Sinne der Story wäre ja man landete am Ende bei 100%. Dann bestätigt einem die Grafik am Ende stets das, woran man sowieso schon glaubte. Oder gibt es für die 50% einen Grund, der mir entgangen wäre?

Graphen in Polarkoordinaten

Wie auch immer der heutige xkcd gemeint sein mag, Polarkoordinaten sind jedenfalls eine nützliche Sache, oft sehr praktisch, wenn man in der Ebene rechnen will.

Und viele Bilder lassen sich in Polarkoordinaten besser beschreiben als in kartesischen.
Angefangen mit dem Kreis r=1

(in kartesischen Koordinaten zusammengesetzt aus den Graphen von und )

über die logarithmische Spirale r=e^φ

oder r=2sin(4φ)

Graphen in Polarkoordinaten zeichnen kann man mit FooPlot

Kommentare (17)

#1 H.M.Voynich
26. Juni 2013

“Oder gibt es für die 50% einen Grund, der mir entgangen wäre?”

Vermutlich das Wörtchen “clockwise”.
#2 Thilo
26. Juni 2013

Verstehe ich nicht, wenn man im Uhrzeigersinn weiterläuft wird’s nicht besser.
#3 haarigertroll
26. Juni 2013

Wenn die x- und die y-Achse gleich skaliert sind, dann beginnt man doch bei 50% und kommt nach einer Drehung im Uhrzeigersinn am Ende bei 100% raus, oder sehe ich das falsch?
#4 Martin Windischer
26. Juni 2013

Mit “clockwise” ist vermutlich gemeint, dass man mit φ=90° beginnt, und der Winkel kleiner wird, bis φ=0°
#5 rolak
27. Juni 2013

Wo ist das Problem? Titel ist ja “Wahrscheinlichkeit dafür daß dies Bild ein Uhrzeigersinn-Polarkoordinaten-Graph ist…” (also wie in der Navigation: 0° bzw 360° ist Norden bzw ‘oben’). Jibbet sich zwei Fälle:

a) Betrachter nimmt kartesische Koordinaten an. W. fängt an bei ‘unentschieden’ und entwickelt sich mit steigendem x zu 0%-Polar, also kartesisch.
b) Betrachter nimmt Polarkoordinaten an. W fängt an bei ‘unentschieden’ und entwickelt sich mit steigendem φ zu 100%, also polar.

Kurz gesagt: Der Graph bestätigt des Betrachters Annahme, egal wofür er sich entschieden hatte. Ist doch ne schöne Spielerei.
#6 Frank Wappler
https://play.nice--score.twice
27. Juni 2013

Nette Spielerei, sofern man einen Grund für
$P[ t ] == P[ t + 2 \pi k ], k \in {\mathbb{Z}}$
hat;
oder nicht über $t \in \{ P{-1}[ 100 % ] ... 4 P{-1}[ 50 % ] \}$ hinaus spielt …

p.s.
Thilo schrieb (Juni 26, 2013):
> Und viele Bilder lassen sich in Polarkoordinaten besser beschreiben als in kartesischen.

Viele Bilder lassen sich am besten koordinatenfrei beschreiben; angefangen mit dem Kreis:

$K | a, b, p, q \in K \rightarrow$
$2 + 2 \left( \frac{ap}{ab} \right)^2 + 2 \left( \frac{ap}{bp} \right)^2 – \left( \frac{ab}{bp} \right)^2 – \left( \frac{bp}{ab} \right)^2 – \left( \frac{ap}{ab} \right)^2 \left( \frac{ap}{bp} \right)^2 =$
$\left(\frac{ap}{bq}\right)^2 \left( 2 + 2 \left( \frac{bq}{bp} \right)^2 + 2 \left( \frac{bq}{pq} \right)^2 – \left( \frac{bp}{pq} \right)^2 – \left( \frac{pq}{bp} \right)^2 – \left( \frac{bq}{bp} \right)^2 \left( \frac{bq}{pq} \right)^2 \right)$ .
#7 Frank Wappler
https://insert.personalized.comment.preview.request.here
27. Juni 2013

$K | a, b, p, q \in K \rightarrow$
$2 + 2 ( \frac{ap}{ab} )^2 + 2 ( \frac{ap}{bp} )^2 – ( \frac{ab}{bp} )^2 – ( \frac{bp}{ab} )^2 – ( \frac{ap}{ab} )^2 ( \frac{ap}{bp} )^2 =$
$( \frac{ap}{bq} )^2 ( 2 + 2 ( \frac{bq}{bp} )^2 + 2 ( \frac{bq}{pq} )^2 – ( \frac{bp}{pq} )^2 – ( \frac{pq}{bp} )^2 – ( \frac{bq}{bp} )^2 ( \frac{bq}{pq} )^2 )$ .
#8 Frank Wappler
https://insert.personalized.comment.preview.request.here
27. Juni 2013

Nette Spielerei, sofern man einen Grund für
$P[ t ] == P[ t + 2 \pi k ], k \in {\mathbb{Z}}$
hat;
oder nicht über $t \in \{ P^{-1}[ 100 % ] ... 4 P^{-1}[ 50 % ] \}$ hinaus spielt …

p.s.
Thilo schrieb (Juni 26, 2013):
> Und viele Bilder lassen sich in Polarkoordinaten besser beschreiben als in kartesischen.

Viele Bilder lassen sich am besten koordinatenfrei beschreiben; angefangen mit dem Kreis:

$2 + 2 \left( \frac{ap}{ab} \right)^2 + 2 \left( \frac{ap}{bp} \right)^2 – \left( \frac{ab}{bp} \right)^2 – \left( \frac{bp}{ab} \right)^2 – \left( \frac{ap}{ab} \right)^2 \left( \frac{ap}{bp} \right)^2 =$
$\left(\frac{ap}{bq}\right)^2 \left( 2 + 2 \left( \frac{bq}{bp} \right)^2 + 2 \left( \frac{bq}{pq} \right)^2 – \left( \frac{bp}{pq} \right)^2 – \left( \frac{pq}{bp} \right)^2 – \left( \frac{bq}{bp} \right)^2 \left( \frac{bq}{pq} \right)^2 \right)$ .
#9 Thilo
27. Juni 2013

@Frank Wappler: irgendwas ist mit den LaTex-Befehlen nicht in Ordnung, ich finde aber den Fehler nicht.
#10 Frank Wappler
https://play.nice--score.twice
27. Juni 2013

Nette Spielerei, sofern man einen Grund für
$P[ t ] == P[ t + 2 \pi k ], k \in {\mathbb{Z}}$
hat;
oder nicht über
$t \in \{ P^{-1}[ 100 \% ] ... 4 P^{-1}[ 50 \% ] \}$
hinaus spielt …

p.s.
Thilo schrieb (Juni 26, 2013):
> Und viele Bilder lassen sich in Polarkoordinaten besser beschreiben als in kartesischen.

Viele Bilder lassen sich am besten koordinatenfrei beschreiben; angefangen mit dem Kreis:

$2 + 2 \left( \frac{ap}{ab} \right)^2 + 2 \left( \frac{ap}{bp} \right)^2 – \left( \frac{ab}{bp} \right)^2 – \left( \frac{bp}{ab} \right)^2 – \left( \frac{ap}{ab} \right)^2 \left( \frac{ap}{bp} \right)^2 =$
$\left(\frac{ap}{bq}\right)^2 \left( 2 + 2 \left( \frac{bq}{bp} \right)^2 + 2 \left( \frac{bq}{pq} \right)^2 – \left( \frac{bp}{pq} \right)^2 – \left( \frac{pq}{bp} \right)^2 – \left( \frac{bq}{bp} \right)^2 \left( \frac{bq}{pq} \right)^2 \right)$ .
#11 Frank Wappler
https://rapid.hindsight.inc
27. Juni 2013

Thilo schrieb (#9, 27. Juni 2013):
> irgendwas ist mit den LaTex-Befehlen nicht in Ordnung, ich finde aber den Fehler nicht.

Danke für die rasche Rückmeldung (und Entschuldigung für meine Fehlversuche; insbesondere die z.Z. vorliegenden #7 und #8 bei Gelegenheit bitte löschen.).

Aber was mit den LaTeX-Befehlen nicht in Ordnung ist, ist ja sehr offensichtlich:
denen fehlt die ScienceBlogs-Kommentarvorschau!
#12 Frank Wappler
https://testing.testing--zwölf.zwölf...
27. Juni 2013

Was ich schon in den z.Z. vorliegenden Fehlversuchen #7 und #8 vergeblich versucht hatte:

$K | a, b, p, q \in K \rightarrow$
$2 + 2 ( \frac{ap}{ab} )^2 + 2 ( \frac{ap}{bp} )^2 – ( \frac{ab}{bp} )^2 – ( \frac{bp}{ab} )^2 – ( \frac{ap}{ab} )^2 ( \frac{ap}{bp} )^2 =$
$( \frac{ap}{bq} )^2 ( 2 + 2 ( \frac{bq}{bp} )^2 + 2 ( \frac{bq}{pq} )^2 – ( \frac{bp}{pq} )^2 – ( \frac{pq}{bp} )^2 – ( \frac{bq}{bp} )^2 ( \frac{bq}{pq} )^2 )$ .
#13 rolak
28. Juni 2013

Mensch Wappler, das ist (auch Dir) schon x-mal gesagt worden: Statt hier rumzuspammen nutze gefälligst eine Plattform mit angemessener Vorschau (zB). WP-angepasste Hilfe zu Latex gibts bei WP, wirste doch hoffenbtlich selber finden? Hier ist ja typischerweise bei drei urls modtime, soll Thilo nicht für arbeiten müssen.
#14 michael
28. Juni 2013

> …eine Plattform mit angemessener Vorschau …

Eine weitere Platform mit Anschnauz Funktionalität wird sich aber so leicht nicht findem lassen.
#15 Frank Wappler
https://Any.sufficiently.advanced.functionality.is.indistinguishable.from.a.bug.
28. Juni 2013

rolak schrieb (28. Juni 2013):
> Mensch Wappler, das ist (auch Dir) schon x-mal gesagt worden: […]nutze gefälligst eine Plattform mit angemessener Vorschau

Ich weiß nicht, wo das zu lesen gewesen sein soll (sonst hätte ich bestimmt umgehend nach einer entsprechenden Empfehlung gefragt).
Zu den direkten entsprechenden Anfragen (nicht nur von mir) und hoffnungsvoll – vagen Kenntnisnahmen gab’s dort bisher offenbar keine Rückmeldung.

> (zB [https://agyon.de/produkte/synchronisationsstrahlsynchonisierer/] )

Danke für die Empfehlung! Das probier ich mal aus …
Ergebnis: meine originale Formel (#12, 27. Juni 2013) wurde in der dortigen Vorschau ebenso wie hier im Kommentar geparst (d.h. in wesentlichen Teilen gar nicht).

Nachdem wiederholte Nutzung der empfohlenen (und tatsächlich vorhandenen und nutzbaren!) Vorschaufunktion mir erlaubte, meinen Fehler einzugrenzen, aufzufinden und soweit zu beheben, dass mir die Vorschau dort nun die korrigierte Formel vollständig geparst zeigte (zzgl. weniger bedeutender Formatierungsänderungen, über die ich erst anhand der geparsten Formel entscheiden konnte) – schau’n wir mal hier:

Thilo schrieb (Juni 26, 2013):
> Und viele Bilder lassen sich in Polarkoordinaten besser beschreiben als in kartesischen.

Viele Bilder lassen sich am besten koordinatenfrei beschreiben; angefangen mit dem Kreis:

$K | a, b, p, q \in K \rightarrow$

$\left(2 + 2 \, ( \frac{ap}{ab} )^2 + 2 \, ( \frac{ap}{bp} )^2 - ( \frac{ab}{bp} )^2 -( \frac{bp}{ab} )^2 -( \frac{ap}{ab} )^2 ( \frac{ap}{bp} )^2 \right) ( \frac{bq}{ap} )^2 =$

$2 + 2 \, ( \frac{bq}{bp} )^2 + 2 \, ( \frac{bq}{pq} )^2 -( \frac{bp}{pq} )^2 - ( \frac{pq}{bp} )^2 - ( \frac{bq}{bp} )^2 ( \frac{bq}{pq} )^2$ .
#16 Ben
4. Juli 2013

“Verstehe ich nicht, wenn man im Uhrzeigersinn weiterläuft wird’s nicht besser.”

Mit clockwise meinen die, dass man nicht wie normal gegen den uhrzeigersinn den ‘zeiger’ dreht sondern halt von 0° (auf 12 uhr) im uhrzeigersinn bis hier auf 90° (3 uhr). Somit geht die chance von 50% auf 100%.
#17 情趣用品
22. Juli 2013

Thank you for the suggestions posed within this post. They have offered me a fresh outlook on this subject. I appear forward to researching much more.

SPAM link removed