Schon die Babylonier hatten vor 3600 Jahren eine Formel, mit der sie unendlich viele ganzzahlige Lösungen der Gleichung x2+y2=z2 finden konnten. Diophantus bewies später, dass man alle Lösungen aus der Formel der Babylonier erhält. Im 17. Jahrhundert entwickelte Pierre de Fermat die Methode des unendlichen Abstiegs, um zu bewiesen, dass es keine positiven ganzzahligen Lösungen von x4+y4=z4 gibt und an den Rand seiner im Nachlaß aufgefundenen Kopie von Diophantus’ Arithmetica schrieb er die Behauptung, dass er auch die Unmöglichkeit von positiven ganzzahligen Lösungen von xn+yn=zn für n>2 beweisen könne.
Die Suche nach diesem Beweis wurde für mehr als 350 Jahre eine treibende Kraft der Zahlentheorie. Euler löste den Fall n=3, Legendre und Dirichlet unabhängig voneinander den Fall n=5. Ein fehlerhafter Beweis führte im 19. Jahrhundert zur Theorie der Kreisteilungskörper und letztlich zur Entwicklung der Idealtheorie. Der Fehler hatte in der Annahme gelegen, dass man im Ganzheitsring gewisser Zahlkörper eine eindeutige Primfaktorzerlegung habe. Das ist aber nicht der Fall oder jedenfalls erst, wenn man gewisse ideale Zahlen hinzunimmt. Die idealen Zahlen entsprechen aus heutiger Sicht Idealen im Ganzheitsring, welche keine Hauptideale sind. (Hauptideale entsprechen den ganzen Zahlen des Zahlkörpers.) Die eindeutige Primärzerlegung in allgemeinen Noetherschen Ringen ist der Inhalt des Lasker-Noether-Theorems.
Spätestens seitdem am Beginn des 20. Jahrhunderts ein an Multipler Sklerose erkrankter Bankierssohn, Arzt und Mathematiker 100000 Goldmark aus seinem Nachlaß auf den Beweis aussetzte, beschäftigten sich auch viele Laien mit dem Problem. Das änderte sich auch nicht mit der inflationsbedingten Entwertung auf wenige Reichsmark. (Immerhin wurden es später wieder 70000 Mark.) Für die zuständigen Göttinger Mathematiker war es nicht immer leicht, die Laien von der Unstimmigkeit der gemachten Annahmen und der oft komplizerten formellen Berechnungen zu überzeugen.
Ernstzunehmende Beweisversuche folgten bis in die 1970er Jahre mehr oder weniger dem aus dem 19. Jahrhundert bekannten Ansatz der Untersuchung der Idealklassengruppen von Kreisteilungskörpern. Die Frage gehörte aber nicht mehr zu den zentralen Problemen der Mathematik. Immerhin wurde mit Computerhilfe (unter Weiterentwicklung der Methoden des vorigen Jahrhunderts) für immer größere Werte von n das Problem gelöst.
Mitte der 80er Jahre verbreitete sich dann der Vorschlag Gerhard Freys, zu einer hypothetischen Lösung der Fermat-Gleichung a
n+b
n=c
n die elliptische Kurve y
2=x
3+(a
n-b
n)x
2-a
nb
nx zu betrachten. Wenn n eine ungerade Primzahl ist, dann erhält man eine semistabile elliptische Kurve, die nicht modular zu sein scheint. Diese Kurven waren Ende der 60er Jahre in mehreren Arbeiten von Hellegouarch untersucht worden, der ebenso wie unabhängig Demjanenko erkannte, dass ein Torsionspunkt der Ordnung 2n
2 zu einer nichttrivialen Lösung der ursprünglichen Fermat-Gleichung führt. Gerhard Frey hatte dann die Idee gehabt, das Fermat-Problem auf die Modularität besagter elliptischen Kurve zurückzuführen.
Die Modularität elliptischer Kurven war in den 50er Jahren von Taniyama vermutet worden. Martin Eichler hatte zuvor in einer Arbeit über die elliptische Kurve y2+y=x3-x2 festgestellt, dass für Primzahlen p die Anzahl ap ihrer Punkte über dem Körper Fp gerade der Koeffizient von xp in der Reihenentwicklung des unendlichen Produkts 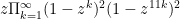
Die Vermutung besagt, dass für die L-Reihe einer elliptischen Kurve – welche eine damals bereits etablierte Art war, die ap in einer einzigen Funktion zu kodieren – mit der Heckeschen L-Reihe einer geeigneten Modulform übereinstimmt. (Genauer: einer geeigneten Spitzenform vom Gewicht 2 mit ganzzahligen Fourier-Koeffizienten.) Eine äquivalente komplex-analytische Formulierung der Vermutung besagt: für jede elliptische Kurve E mit Führer N gibt es eine nichtkonstante holomorphe Abbildung X0(N)—>E. Dabei ist X0(N) die Kompaktifizierung (durch Hinzufügen der Spitzen) von Y0(N)=Γ0(N)\H2, dem Quotienten der hyperbolischen Ebene nach der Hecke-Kongruenzgruppe Γ0(N).

Kommentare (3)