Theorema Magnum MXMV: der große Satz von Fermat

Ernstzunehmende Beweisversuche folgten bis in die 1970er Jahre mehr oder weniger dem aus dem 19. Jahrhundert bekannten Ansatz der Untersuchung der Idealklassengruppen von Kreisteilungskörpern. Die Frage gehörte aber nicht mehr zu den zentralen Problemen der Mathematik. Immerhin wurde mit Computerhilfe (unter Weiterentwicklung der Methoden des vorigen Jahrhunderts) für immer größere Werte von n das Problem gelöst.

Mitte der 80er Jahre verbreitete sich dann der Vorschlag Gerhard Freys, zu einer hypothetischen Lösung der Fermat-Gleichung an+bn=cn die elliptische Kurve y2=x3+(an-bn)x2-anbnx zu betrachten. Wenn n eine ungerade Primzahl ist, dann erhält man eine semistabile elliptische Kurve, die nicht modular zu sein scheint. Diese Kurven waren Ende der 60er Jahre in mehreren Arbeiten von Hellegouarch untersucht worden, der ebenso wie unabhängig Demjanenko erkannte, dass ein Torsionspunkt der Ordnung 2n2 zu einer nichttrivialen Lösung der ursprünglichen Fermat-Gleichung führt. Gerhard Frey hatte dann die Idee gehabt, das Fermat-Problem auf die Modularität besagter elliptischen Kurve zurückzuführen.

Die Modularität elliptischer Kurven war in den 50er Jahren von Taniyama vermutet worden. Martin Eichler hatte zuvor in einer Arbeit über die elliptische Kurve y²+y=x³-x² festgestellt, dass für Primzahlen p die Anzahl a_p ihrer Punkte über dem Körper F_p gerade der Koeffizient von x^p in der Reihenentwicklung des unendlichen Produkts 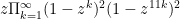ist. Dieses Produkt ist eine Modulform. Taniyama fand einige weitere Modulformen, deren Koeffizienten zu einer elliptischen Kurve gehören. Auf einem Symposium in Tokio schlug er eine allgemeine Vermutung vor, die aber nicht korrekt war. Shimura gab eine korrigierte Formulierung und propagierte im weiteren die Vermutung über die Entsprechung zwischen elliptischen Kurven und Modulformen.

Die Vermutung besagt, dass für die L-Reihe einer elliptischen Kurve – welche eine damals bereits etablierte Art war, die a_p in einer einzigen Funktion zu kodieren – mit der Heckeschen L-Reihe einer geeigneten Modulform übereinstimmt. (Genauer: einer geeigneten Spitzenform vom Gewicht 2 mit ganzzahligen Fourier-Koeffizienten.) Eine äquivalente komplex-analytische Formulierung der Vermutung besagt: für jede elliptische Kurve E mit Führer N gibt es eine nichtkonstante holomorphe Abbildung X₀(N)—>E. Dabei ist X₀(N) die Kompaktifizierung (durch Hinzufügen der Spitzen) von Y₀(N)=Γ₀(N)\H², dem Quotienten der hyperbolischen Ebene nach der Hecke-Kongruenzgruppe Γ₀(N).

Die meisten Mathematiker außerhalb Japans waren skeptisch. André Weil meinte, für die Vermutung spreche nicht viel mehr als dass elliptische Kurven und Modulformen jeweils abzählbare Mengen bildeten und so gesehen nichts gegen eine Bijektion zwischen beiden spreche.

Ende der 60er Jahre, bemerkenswerterweise durch den zuvor skeptischen André Weil, erwachte wieder das Interesse an der Taniyama-Shimura-Vermutung. Weil zeigte, dass sie aus der vermuteten Funktionalgleichung der getwisteten L-Funktion der elliptischen Kurve folgen würde und dass der Führer der elliptischen Kurve der Grad der Modulform sein müsse. Damit konnte man die Vermutung nun an Beispielen testen und die Mathematiker waren plötzlich überzeugt von ihrer Richtigkeit. Einige numerische Beobachtungen würden sich mit dieser Vermutung nun erklären lassen. Zum Beispiel hatte man beobachtet, dass der Führer einer elliptischen Kurve über Q mindestens 11 ist. Dies würde mit der Modularitätsvermutung folgen, weil die Modulkurve X₀(N) für N<11 Geschlecht 0 hat und damit nicht auf eine elliptische Kurve abbilden kann. Wenig später wurde die Vermutung Teil des viel allgemeineren Langlands-Programms. Freys Idee einer Anwendung der Modularitätsvermutung auf das Fermat-Problem, die er seit den 70er Jahren vielen Kollegen erzählte, beeindruckte diese zunächst aber wenig. Sie sahen den Zusammenhang eher als Indiz dafür, dass die Vermutung über die Modularität elliptischer Kurven ebenso schwer sein sollte wie die unzugängliche Fermat-Gleichung. Neukirch überzeugte Frey schließlich 1986, seine Idee aufzuschreiben. Die dreiseitige Notiz verbreitete sich unter Zahlentheoretikern und gelangte auch zu Jean-Pierre Serre. Der fand schnell einen Fehler im Argument, erkannte aber, dass das Argument jedenfalls zeigt, dass die zur elliptischen Kurve assoziierte Darstellung modulo n sehr wenig verzweigt ist. Das erinnerte ihn an Vermutungen, die er vor längerer Zeit einmal aufgestellt (aber nur in Spezialfällen publiziert) hatte und er machte sich klar, dass diese Vermutungen jedenfalls völlig ausreichen würden, um Freys Argument zu rechtfertigen. Ribet hörte bald darauf von dieser sogenannten ε-Vermutung und bewies sie bei einem Gespräch mit Mazur während des ICM in Berkeley. Damit wußte man also, dass die Fermat-Vermutung aus der Modularität der Frey-Hellegouarch-Kurve folgen würde.
Modularität elliptischer Kurven kann man im größeren Kontext von Galois-Darstellungen sehen. Bekanntlich läßt sich eine elliptische Kurve als C/L für ein Gitter L realisieren, wobei die Addition der elliptischen Kurve der Addition in C/L entspricht. Insbesondere bilden die l-Torsionspunkte der elliptischen Kurve eine zu (Z/lZ)² isomorphe Untergruppe. Für eine über Q definierte elliptischen Kurve haben die Torsionspunkte Koordinaten im algebraischen Abschluß von Q. 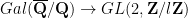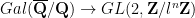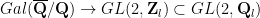Insbesondere wirkt die Galois-Gruppe auf den l-Torsionspunkten, womit man eine Darstellung bekommt. Für alle natürliche Zahlen n kann man dann die lⁿ-Torsionspunkte betrachten, bekommt also eine Darstellung , und damit im projektiven Limes eine Darstellung über den l-adischen Zahlen . Man hat also zu jeder elliptische Kurve eine solche sogenannte Galois-Darstellung.

Galois-Darstellungen kommen in vielen Zusammenhängen in der Zahlentheorie vor. Insbesondere kann man auch gewissen Modulformen Galois-Darstellungen zuordnen: Eine Konstruktion von Deligne gibt zu jeder Spitzenform zur Kongruenzgruppe Γ1(N) eine Galois-Darstellung über einem etwas größeren Körper, nämlich der durch die Koeffizienten der Spitzenform erzeugten Erweiterung von Q tensoriert mit Ql. Für alle Nl nicht teilenden Primzahlen p ist diese Darstellung unverzweigt, und die Spur des Bildes des Frobenius-Automorphismus Frobp ist gerade der Koeffizient ap. Weiterhin ist die Determinante ε0(p)pk-1 für den mit der Spitzenform assoziiierten Charakter ε0 und durch diese Eigenschaften ist die Darstellung bis auf Isomorphismus eindeutig festgelegt.

Allgemein weiß man durch tiefe Sätze von Shimura, Deligne, Mazur und Langlands, dass man jeder Eigenform eines auf einem Raum von Modulformen wirkenden Hecke-Operators eine Galois-Darstellung (sogar über einem endlichen Körper der Ordnung ln) zuordnen kann. Deligne hatte 1972 eine Vermutung von Serre bewiesen, derzufolge man zu Modulformen l-adische Galois-Darstellungen hat. Das hat zahlentheoretische Anwendungen zahlreiche arithmetische Funktionen aus den Koeffizienten von Modulfunktionen oder Modulformen gewonnen werden können. So vermutete er, dass gewisse Kongruenzen der τ-Funktion durch die 2-dimensionalen l-adischen Darstellungen der Galois-Gruppe (für alle l) erklärt werden können, wo man die τ-Funktion als Spur von Frobp erhält. Beispielsweise kann man auf diese Weise die berühmte von Ramanujan gefundene Kongruenz τ(p)=1+p¹¹ mod 691 erklären.

Mit diesem Ansatz war die Modularität elliptischer Kurven dann Teil des Langlands-Programms geworden. Ein wichtiger Vorteil war die Analogie zu Modulfomen vom Gewicht 1: hier kann man das Bild durch 2-dimensionale komplexe Darstellungen ersetzen, deren Konstruktion 1974 von Deligne und Serre gegeben worden war, und die wesentliche Umkehrung für auflösbare Darstellungen war ein Spezialfall von Langlands Reziprozitätsvermutung für Artinsche L-Funktionen (nämlich die Holomorphie der Zetafunktion für nichttriviale Darstellungen), er wurde von Langlands in seinem Buch “Basiswechsel für GL(2)” (mit einigen Details in einer Arbeit von Tunnell) bewiesen. Das war der erste nichtelementare Fortschritt zur Artin-Vermutung, welche Holomorphie Artinscher L-Funktionen behauptet. 1987 hatte Serre dann eine Modularitätsvermutung aufgestellt: jede (absolut irreduzible, stetige und ungerade) Galois-Darstellung über einem endlichen Körper soll auf diese Weise durch eine Darstellung im Raum der Spitzenformen (in der Charakteristik des endlichen Körpers und mit Koeffizienten im endlichen Körper) gegeben sein. Die Wirkung der Galois-Gruppe ist durch Hecke-Operatoren und es gelten die obigen Formeln für Spur und Determinante. Diese Vermutung ist stärker als die Modularität elliptischer Kurven.

Auch den im 19. und 20. Jahrhundert lange verfolgten Ansatz über die Klassenzahl zyklotomischer Körper kann man als Frage über Galois-Darstellungen interpretieren. Zum Beispiel ist die Bestimmung der Klassenzahl von 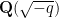äquivalent zur Berechnung des Kerns eines gewissen Homomorphismus in der Kohomologie mit Koeffizienten in einer Galois-Darstellung. Obwohl es bei solchen Problemen viel Fortschritt gab, hatten sich keine überzeugenden Vermutungen gefunden, aus denen der große Satz von Fermat folgen würde. Letztlich würde der Beweis aus einer anderen Quelle kommen, obwohl er auch auf einer verallgemeinerten Klassenzahlformel beruhte.

Bewiesen wurde die Modularität der Frey-Hellegouarch-Kurve und damit der große Satz von Fermat dann von Andrew Wiles mit Unterstützung von Richard Taylor. Sein Beweis benutzte so ziemlich alles, was in den letzten Jahren an neuen Methoden entwickelt worden war – einen “postmodernen Beweis” nannte es Mumford später. Aber er benutzte nicht nur die neuentwickelten Methoden, er führte alles immer noch etwas weiter als jeder andere und fand verblüffende Tricks, wenn die Methoden zu versagen schienen.

Sein Zugang war nicht über elliptische Kurven, sondern über Galois-Darstellungen. Er wollte also zeigen, dass jedes kompatible System l-adischer Galois-Darstellungen von einer Neuform vom Gewicht 2 mit rationalen Koeffizienten auf Γ0(N) kommt. Tatsächlich betrachtete er Formen auf Γ1(N) und schränkte sich auf l-adische Darstellungen für ein einzelnes l ein. Der Beweis begann mit der wesentlichen Beobachtung, dass für jede elliptische Kurve über Q die Darstellung auf den 3-Teilungspunkten modular ist: das folgt unmittelbar aus dem von Langlands und Tunnell bewiesenen Satz. Wenn die Darstellung irreduzibel ist, dann ist jede Hebung zu einer GL(2,Z3)-Darstellung modular (was hier nicht bedeutet, über einem endlichen Körper definiert, sondern von einer Modulform kommend). Das ist Teil einer allgemeineren Theorie, welche Bedingungen beschreibt, unter denen Hebungen modularer Darstellungen modular sind und folgt aus einer überraschenden Verbindung zu einer verallgemeinerten Klassenzahlformel. Letztlich erhält er Modularität für alle elliptischen Kurven von semistabilem Typ, d.h. im Wesentlichen nur Doppelpunkte als Singularitäten nach Reduktion modulo Primzahlen, was für den Beweis der Fermat-Vermutung ausreicht (Faltings formulierte: “wenn man Glück hat, ist die Hebung modular, wenn nicht, zeigt man, dass die Kurve nicht semistabil ist“).

Den ersten, letztlich noch nicht korrekten Beweis hatte Andrew Wiles im Juli 1993 auf einer Tagung in Cambridge vorgetragen. Man hatte ihn eine dreiteilige Vortragsreihe halten lassen, deren Zuhörer zunächst nicht wußten, worum es gehen würde. Am zweiten Tag verdichteten sich dann aber doch die Gerüchte. Immer mehr Zuhörer machten während des dritten Vortrags Fotos, so dass der Raum schließlich mehr einem Premierentheater als einem Vortragssaal glich. Nach dem Ende seines Vortrags wurde die Nachricht per Fax und e-Mail um die Welt geschickt.

Als nach einigen Monaten kein Manuskript vorlag, mehrten sich kritische Stimmen und Gerüchte. Im Dezember, ein halbes Jahr nach seiner Vortragsreihe und kurz nach einem Artikel in “Le Monde”, schrieb Wiles eine e-Mail an zahlreiche Kollegen: „Wegen der Spekulationen möchte ich kurz berichten. Während des Reviews gab es verschiedene Probleme. Die meisten konnten gelöst werden, aber eines nicht. Die Berechnung einer oberen Schranke für eine Selmer-Gruppe ist noch nicht fertig. Ich glaube, dass ich das bald mit den Ideen aus meinem Cambridge-Vortrag fertigstellen kann. Deshalb gibt es noch kein Preprint. Im Februar halte ich Vorträge in Princeton.“

Wiles hielt den Vortrag in Princeton und verteilte maschinengeschriebene Seiten. Der Vortrag endete mit dem Resultat, dass es unendlich viele j-Invarianten gibt, deren zugehörige elliptische Kurven modular sind. Die Vorträge sollten im Herbst fortgeführt werden. Richard Taylor, sechs Jahre zuvor bei Wiles promoviert hatte und inzwischen in Oxford arbeitete, sagte etwas über den schwierigeren Teil, aber auf Geheiß Wiles wurde die Zirkulation von Mitschriften untersagt. Taylor kehrte dann für einige Zeit nach Princeton zurück, um Wiles beim Schließen der Beweislücke zu helfen. So richtig glaubte niemand mehr an den Erfolg, zu oft war in der Vergangenheit schon ein Beweis der Fermat-Vermutung angekündigt worden.

Auf dem ICM August 1994 in Zürich durfte Wiles den Schlußvortrag halten, er hatte aber keinen Beweis der Fermat-Vermutung. Eine Fields-Medaille hätte er ohnehin nicht bekommen können, denn mit 41 war er ein Jahr zu alt. Einige Wochen nach dem Kongreß gelang es Wiles und Taylor dann doch, zwar nicht die Lücke im Beweis zu schließen, aber für den fehlerhaften Teil einen neuen, anderen Beweis zu finden, was sie aber zunächst noch nicht öffentlich machten. Faltings, gerade zum Direktor des Max-Planck-Instituts in Bonn berufen, meinte unterdessen, die Lücke im ursprünglichen Beweis schließen zu können und skizzierte seinen Plan in der Ankündigung einer Sommerschule über elliptische Kurven, die er mit Harder halten wollte. Am ersten Tag der Sommerschule erhielten sie morgens eine zur weiteren Verbreitung bestimmte e-Mail eines Mathematikers, das der besagte Teil im Beweis entfällt und durch einen anderen ersetzt wird. Faltings hielt dann auf der Sommerschule fünf Vorträge, wo er mit einigen Vereinfachungen im Wesentlichen Wiles und Taylor folgte.

Es dauerte einige Zeit, bis das Manuskript herauskam, das zunächst nur wenige Eingeweihte erhielten, was zu neuen Verstimmungen führte. Als Resultat hatte man vor allem, dass die L-Funktion einer (semistabilen) elliptischen Kurve eine Funktionalgleichung mit erfüllt. Veröffentlicht wurde Wiles‘ Arbeit „Modular elliptic curves and Fermat‘s last theorem“ und die gemeinsame Arbeit von Wiles-Taylor „Ring-theoretic properties of certain Hecke algebras“ 1995 in den Annals of Mathematics.