Je älter man ist, desto höher ist statistisch gesehen das Risiko, zu sterben. Das ist trivial. Deswegen interessiert beim Vergleich von Sterberaten, z.B. zwischen zwei Landkreisen, oft nicht allein die rohe Sterberate, also die Zahl der Gestorbenen bezogen auf die Einwohner/innen, sondern man möchte die Sache auch altersbereinigt haben. Dann sieht man, ob sonst noch etwas im Spiel ist.
Alte und junge Regionen und eine etwas unbekannte Geschichte des kalten Krieges
Ein Beispiel: Im Landkreis Wunsiedel im nordöstlichen Oberfranken lag die rohe Sterberate 2010 bei 1.427,6 je 100.000 Einwohner/innen, im Landkreis Freising dagegen, Nähe München, lag sie bei 710,4 je 100.000 Einwohner/innen. Der Anteil der Bevölkerung, die 65 Jahre und älter ist, lag 2010 im Landkreis Wunsiedel bei 25,4 %, im Landkreis Freising bei 15,3 %. Wunsiedel ist der älteste Landkreis Bayerns, Freising der jüngste. Kein Wunder also, dass die Sterberate in Wunsiedel höher ist als die in Freising.
Aber das ist noch nicht die ganze Geschichte. Man kann jetzt altersbereinigte Sterberaten berechnen, d.h. eine Altersstandardisierung vornehmen. Bei einer Altersstandardisierung anhand der sog. „alten Europastandardbevölkerung“ errechnet sich für Wunsiedel eine altersbereinigte Sterberate von 620,9 je 100.000, für Freising kommt man auf 507,3 je 100.000. Das sieht schon besser für Wunsiedel aus, aber es hat offenkundig auch altersbereinigt eine höhere Sterberate, für die demnach andere Ursachen verantwortlich sein müssen. In diesem Fall spielen die sozioökonomischen Rahmenbedingungen der Region eine wichtige Rolle. Nordostbayern war lange Zeit „Zonenrandgebiet“, wie es so schön hieß, eine Region ohne wirtschaftliches Hinterland. Schlechtere sozioökonomische Lage bedeutet höhere Sterblichkeit, ein altes Gesetz der Sozialepidemiologie. In den Sterberaten Nordostbayerns machen sich die Folgen der europäischen Teilung bis heute bemerkbar.
Altersstandardisierung, leicht gemacht
Das war Geschichte, aber immer noch nicht die, die ich eigentlich erzählen will. Bevor das kommt, muss ich ein paar trockene Vorübungen machen und die Verfahren der Altersstandardisierung erklären. Man unterscheidet dabei im Wesentlichen zwei Methoden, die direkte und die indirekte Altersstandardisierung. Bei der direkten Altersstandardisierung gewichtet man die altersspezifischen Sterberaten einer Untersuchungspopulation mit den altersspezifischen Kopfzahlen einer Standardbevölkerung. Damit unterstellt man für die Vergleichsregionen einen gleichen Altersaufbau. Für viele Zwecke, z.B. für europäische Vergleiche, ist die schon erwähnte „alte Europastandardbevölkerung“ gebräuchlich. Man kann aber z.B. auch die deutsche Bevölkerung des Jahres 2010 nehmen, oder die bayerische des Jahres XY. Es kommt nur darauf an, für alle Vergleichsregionen die gleiche Standardbevölkerung zu nehmen.
Bei der indirekten Altersstandardisierung geht man in gewisser Weise umgekehrt vor. Man nimmt die altersspezifischen Sterberaten einer Standardpopulation, z.B. der bayerischen, und gewichtet diese mit den altersspezifischen Bevölkerungszahlen der Untersuchungspopulation, z.B. des Landkreises Freising. Daraus ergeben sich „erwartete Sterbefälle“, nämlich die Zahl der Sterbefälle, die in Freising zu erwarten wäre, wenn in Freising mit seinem Altersaufbau die gleichen Sterberaten bestehen würden wie in Bayern. Setzt man dann die reale Zahl der Sterbefälle in Freising mit der so berechneten erwarteten Zahl ins Verhältnis, erhält man die „Standardisierte Mortalitätsratio (SMR)“. Sie gibt an, wie sich die Sterblichkeit Freisings zu der Bayerns verhält. Ist die Sterblichkeit gleich, beträgt die SMR 1. Wäre sie in Freising höher als in Bayern, läge die SMR über 1, andernfalls unter 1. Die Abweichung von der 1 lässt sich als prozentuale Abweichung der Sterblichkeit Freisings von der Bayerns interpretieren.
Im Jahr 2010 lag die SMR Freisings bei 0,95, d.h. Freising hat altersbereinigt eine um 5 % geringere Sterblichkeit als Bayern. Für den Landkreis Wunsiedel errechnet sich eine SMR von 1,12, also eine um 12 % höhere Sterblichkeit als im bayerischen Durchschnitt.
Man erkennt sofort, wo der Vorteil der indirekten Altersstandardisierung liegt: Man hat für die SMR die Altersverteilung der Sterbefälle in Freising nicht verwendet. Bei kleinen Fallzahlen oder einer unsicheren Altersverteilung der Fälle ist das die Methode der Wahl. Der Nachteil liegt ebenfalls auf der Hand: In der SMR ist der Altersaufbau Bayerns bereinigt, d.h. der SMR liegt der Altersaufbau Freisings zugrunde. Das hat zur Folge, dass die indirekte Altersstandardisierung immer nur im Zweierverhältnis Untersuchungspopulation – Standardpopulation zu einem altersbereinigten Vergleich führt. Die SMR Freisings und die SMR Wunsiedels kann man eigentlich so nicht vergleichen, es sei denn, beide Landkreise haben nahezu den gleichen Altersaufbau. Man muss nicht lange googeln, um herauszufinden, dass das oft nicht beherzigt wird.
Altersstandardisierung, schwer gemacht
Wenn man nun zwei Landkreise altersstandardisiert erst nach einer Methode vergleicht, dann nach einer anderen Methode, sollte das zu gleichen Ergebnissen führen. Und weiter: Wenn man bei der direkten Altersstandardisierung, die die Methode der Wahl zum Vergleich vieler Regionen ist, sollten Rangreihen von Landkreisen unabhängig von der Wahl der Standardbevölkerung sehr hoch korrelieren. Kleine Abweichungen der Rangordnung wird man methodenbedingt immer akzeptieren, aber es sollte keine allzu großen Sprünge in der Rangordnung geben. Schließlich soll die Auskunft, ob die Sterberate, die Krebshäufigkeit oder die Unfallrate in einer Population höher ist als in einer anderen, primär nicht von der gewählten Methode der Altersstandardisierung abhängen.
Hier beginnt nun der wirklich spannende Teil der Sache. Im Rahmen eines Methodenprojekts zur Altersstandardisierung habe ich gerade eine Masterarbeit betreut, die untersucht, wie gut die Rangordnungen der bayerischen Landkreise und kreisfreien Städte – bezogen auf die Sterblichkeit – bei verschiedenen Methoden der Altersstandardisierung übereinstimmen. Das Ergebnis ist etwas beunruhigend, weil sich die Ausgangsthese, dass manche Landkreise methodenabhängig recht große Rangsprünge machen, bestätigt hat. Die Ergebnisse der Masterarbeit werden demnächst auf der Jahrestagung der Deutschen Gesellschaft für Sozialmedizin und Prävention zur Diskussion gestellt. Das Methodenprojekt wird in Zusammenarbeit mit einem statistischen Institut noch weitergeführt – wer gute Ideen dazu hat, ist herzlich eingeladen, sie hier zu äußern.

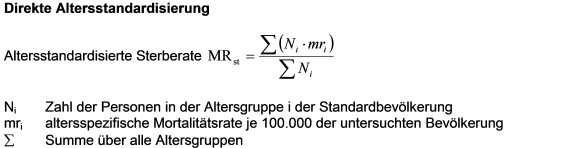
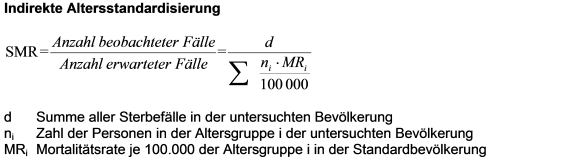



Kommentare (12)