Derzeit wird intensiv darüber diskutiert, ob Deutschland mehr testen muss. Dazu gehört die Frage, wer das bezahlen soll. Wenn größere Gruppen regelmäßig durchgetestet werden, kommen schnell ein paar hundert Millionen Euro zusammen. Private Labors kalkulieren mit Preisen zwischen 100 und 200 Euro.
Am letzten Donnerstag ging das zweite Pandemiegesetz durch den Bundestag. Es sieht vor, dass die gesetzliche Krankenversicherung künftig auch die Kosten für Tests bei nichtsymptomatischen Personen übernimmt, also präventive Tests. Die GKV soll das auch für die Privatversicherten abwickeln, eine interessante Konstruktion. Wenn man so will, attestiert das Bundesgesundheitsministerium der PKV gerade die Systemirrelevanz. Die Refinanzierung der Testkosten soll aus der Liquiditätsreserve des Gesundheitsfonds erfolgen. Die Details sind noch offen, das wird eine Rechtsverordnung regeln, die zeitnah folgen soll.
Damit das Geld nicht sinnlos verpulvert wird, sollte man sich gut überlegen, wen man testet und in welcher Frequenz. Wollte man beispielsweise die mehr als 5 Mio. Beschäftigten im Gesundheitswesen zweimal die Woche durchtesten, kann sich jeder an drei Fingern oder drei Excelzellen ausrechnen, dass das unbezahlbar wäre und auch jede Testkapazität sprengen würde. Da braucht man nicht weiter zu überlegen, ob man zusätzlich auch noch alle Lehrer/innen und Erzieher/innen regelmäßig testen kann oder alle Krankenhausfälle oder alle Menschen in Heimen. Man muss also irgendwie auswählen, sich z.B. auf besonders vulnerable Gruppen konzentrieren oder auf besonders sensible Situationen, z.B. Verlagerungen von Patient/innen zwischen Einrichtungen.
Hinzu kommt, dass ein PCR-Test zum direkten Virennachweis nur eine Momentaufnahme liefert, für ein Zeitfenster kurz nach der Infektion. Erst müssen genug Viren da sein, sonst sieht man noch nichts, dann müssen noch genug Viren da sein, sonst sieht man nichts mehr. Außerdem sollte man beachten, dass die PCR-Methode zwar im Labor sehr genau ist, aber vom Abstrich bis zum Testergebnis doch einige Störungen ins Spiel kommen. In der Literatur wird die klinische Sensitivität der Tests mit ca. 75 % angegeben. Die Sensitivität ist die Wahrscheinlichkeit, mit der ein Test Infizierte erkennt. Die Spezifität wird auf 99 % geschätzt. Sie gibt an, mit welcher Wahrscheinlichkeit der Test Nichtinfizierte erkennt. Wenn man dann noch einen Anhaltspunkt dafür hat, wie hoch die Prävalenz der Infizierten in der Testpopulation ist, kann man ausrechnen, mit welcher Wahrscheinlichkeit ein positives Testergebnis auch wirklich eine Infektion anzeigt.
Nehmen wir dazu einmal an, es würde in der Gesamtbevölkerung getestet. Die Prävalenz beträgt derzeit vielleicht 1 %.* Man wird es erst wissen, wenn die Befunde repräsentativer Studien mit guten Antikörpertests vorliegen. Die Verteilung der Testbefunde unter unseren Annahmen bei einer Testpopulation von 1 Mio. Personen zeigt die folgende Vierfeldertafel:
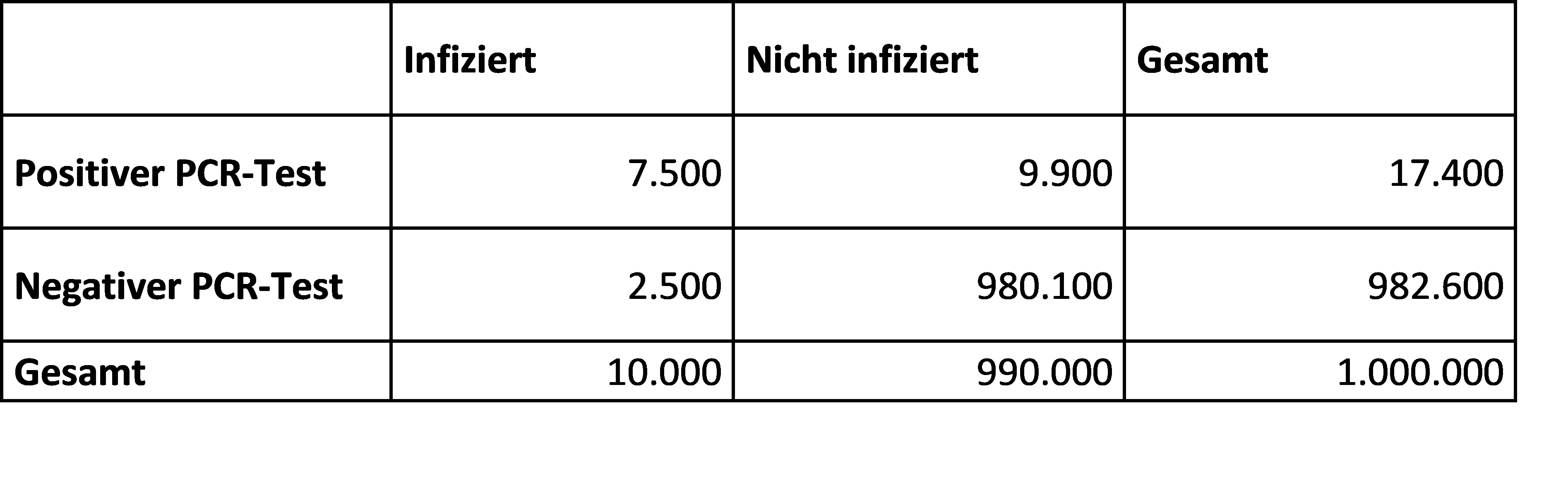
Die Wahrscheinlichkeit, mit der ein positives Testergebnis auch wirklich eine Infektion anzeigt, beträgt damit 7.500/17.400, also ca. 43 %. Diesen Wert nennt man den „positiven prädiktiven Wert“. Anders formuliert: Mehr als jeder zweite positive Test ist bei diesen Ausgangsdaten falsch. Wenn man statt einer Million Testpopulation 10 oder 80 Millionen nimmt, muss man die Zahlen in der Vierfeldertafel nur entsprechend multiplizieren, der positive prädiktive Wert ändert sich durch die Veränderung der Größe der Testpopulation nicht.
Jetzt gibt es allerdings ein paar Punkte zu beachten: Die absolute Zahl der falsch Positiven ist gegenüber der Zahl der durchgeführten Tests sehr klein. Es werden also nicht massenhaft falsch positive Ergebnisse produziert. Und mit Blick auf die Frage, wen man testen soll, ist von hoher Relevanz, ob man eine Gruppe mit niedriger Prävalenz testet oder eine Gruppe mit höherer Prävalenz, etwa in einem Hotspot oder einem durchseuchten Heim. Dann steigt der positive prädiktive Wert sehr schnell deutlich an. Je schlechter die Lage, desto besser für den Test, sozusagen. Wie hoch der positive prädikative Wert etwa für Heinsberg nach der Prävalenzschätzung von ca. 15 % von Herrn Streeck ist, kann sich mit einer Vierfeldertafel jeder selbst einmal ausrechnen. Manche werden vielleicht überrascht sein, wie klein dann der Anteil der falsch positiven Befunde ist. Heute darf man vielerorts ja eh nicht vatertagstypisch mit dem Bollerwagen voller Corona-Bier durch die Landschaft ziehen, Zeit also zum kleinen Einmaleins der Epidemiologie.
————————-
* Nachtrag:
Wie Stefan Wagner unten in Kommentar # 8 richtig anmerkt, dürfte die Prävalenz der aktiven Fälle deutlich unter 1 % liegen, vielleicht um den Faktor 10. Ich bin gedankenlos von der Prävalenz der Immunität ausgegangen, die vor einiger Zeit einmal für Österreich berichtet wurde. Wer will, kann ja auch für diese Variante einmal den ppW ausrechnen. Das Ergebnis wirft einige Fragen auf.
————————-
Zum Weiterlesen:
Beck-Bornholdt H.-P., Dubben, H.-H.: Der Hund, der Eier legt. Frankfurt, rororo, 4. Auflage 2001. Zwar schon etwas älter, aber nach wie vor eins der besten Bücher zum Thema.
Razum, O., Breckenkamp, J., Brzoska, P.: Epidemiologie für Dummies. Weilheim, Wiley, 3. Auflage 2017. Ein didaktisch sehr gut aufgemachtes Lehrbuch.
Kuhn, J., Wildner, M.: Gesundheitsdaten verstehen. Bern, Hogrefe, 2. Auflage 2019. Auch wenn wir nicht direkt auf den positiven prädiktiven Wert eingehen, etwas Eigenwerbung muss sein.




Kommentare (21)