Drüben bei Geograffitico gab es gerade eine Diskussion über eine Publikation des Physikers David Robert Grimes in PLoS ONE über die Lebensdauer von Verschwörungstheorien. Leider ging die Diskussion um Grimes Modell bei Geograffitico unter den Trümmern einer immer seltsamer werdenden Diskussion um die Anschläge auf das World Trade Center verschütt. Ich will das Thema daher hier noch einmal aufgreifen.
Zur Erinnerung: Grimes will zeigen, dass Verschwörungstheorien, insbesondere solche mit viele Beteiligten, schon aus statistischen Gründen keine guten Überlebenschancen haben. Da jeder Mitwisser ein gewisses Aufdeckungsrisiko mit sich trägt, wird, wenn sie nicht schnell genug wegsterben, irgendwann einer plaudern. So weit, so gut. Diese Grundidee wollte er quantitativ unterfüttern und hat dazu das Aufdeckungsrisiko anhand eines Modells auf der Basis der Poisson-Verteilung und dreier konkreter Beispiele berechnet. Die Poisson-Verteilung bildet unter bestimmten Voraussetzungen die Wahrscheinlichkeit des Eintritts von Ereignissen in einem definierten Zeitintervall, z.B. einem Jahr, ab.
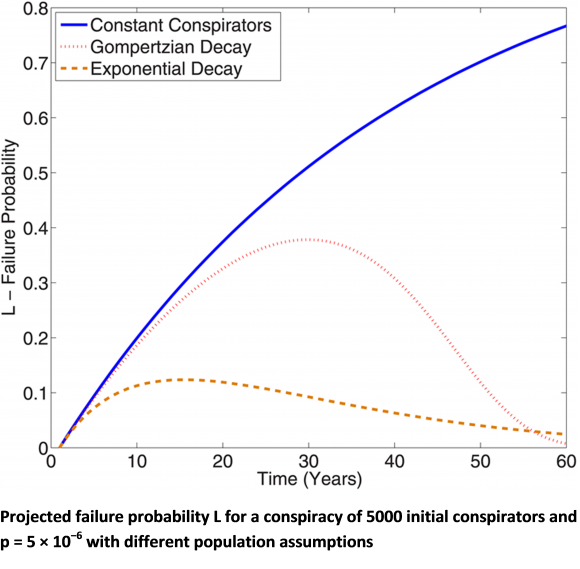
Grimes modelliert nun die Wahrscheinlichkeit, dass eine Verschwörungstheorie aufgedeckt wird und unterscheidet dabei drei Verläufe der Zahl der Mitwisser, einmal, dass sie konstant bleibt und zwei Varianten, bei der die Leute wegsterben (Grimes 2016, Seite 5):
Dann berechnet er, wie lange eine Verschwörungstheorie je nach Zahl der Mitwisser überlebt. Thomas Steinschneider hat in seinem Blog den Artikel von Grimes in mehrfacher Hinsicht kritisiert, angefangen von der Fragwürdigkeit, das Modell mit Daten aus drei Beispielen zu füttern, von denen man nicht weiß, an welcher Stelle in der Verteilung aller Verschwörungen sie stehen, über die Eignung der Poisson-Verteilung für dieses Problem bis hin zum Verlauf der gezeigten Kurven.
Diese Kurven haben mir auch Kopfzerbrechen bereitet. Was zeigen diese Kurven eigentlich? Die Wahrscheinlichkeit, dass die Verschwörung in einem gewissen Zeitintervall (z.B. einem Jahr nach Ablauf von X Jahren) aufgedeckt wird? So hat es, wenn ich ihn richtig verstanden habe, Scienceblogskollege Jürgen Schönstein aufgefasst. Aber warum steigt dann die blaue Linie und verläuft nicht waagrecht? Bleibt die Anzahl der Mitwisser gleich und auch die Wahrscheinlichkeit, mit der eine Person plaudert, müsste auch die Aufdeckungswahrscheinlichkeit in einem definiertem Zeitintervall gleich bleiben. Und warum steigen die beiden anderen Linien erst, bevor sie fallen? Oder sollen die Kurven die Wahrscheinlichkeit zeigen, mit der eine Verschwörungstheorie bis zum Zeitpunkt X aufgedeckt wird? So ist Grimes Artikel angelegt, darauf zielen seine Berechnungen ab und so wurde er überall zitiert. Aber dann müssten alle drei Kurven monoton steigen, weil es um kumulative Wahrscheinlichkeiten geht. Die Wahrscheinlichkeit, dass eine Verschwörungstheorie innerhalb von 10 Jahren aufgedeckt wird, kann nicht kleiner sein als die Wahrscheinlichkeit, dass sie schon innerhalb von 5 Jahren aufgedeckt wird, egal wie viele Mitwisser nach 5 Jahren noch plaudern können. Eine negative Aufdeckungswahrscheinlichkeit kann schließlich nicht dazu kommen. Anders, wenn es um die Wahrscheinlichkeit gehen würde, mit der eine Verschwörungstheorie nach dem Zeitpunkt X aufgedeckt wird: Diese Wahrscheinlichkeit kann natürlich kleiner sein als die der Aufdeckung bis zum Zeitpunkt X. Aber auch hier würde die blaue Kurve nicht ins Bild passen.
Grimes Artikel wurde weltweit rezipiert, vom SPIEGEL bis zur Internetseite der Richard Dawkins-Foundation. Die Geschichte kann auf mehrere Weisen ausgehen:
a) Grimes hat da irgendwas verdreht und das peer review hat es übersehen. Das ist im Moment meine Meinung, so sieht es z.B. auch Thomas Steinschneider.
b) Die Darstellungen bei Grimes sind korrekt, ich stehe nur auf dem Schlauch und der Groschen fällt einfach nicht. Dann habe ich mir – Fasching steht vor der Tür – eine Narrenkappe verdient. Die kann ich mir ja vielleicht mit Thomas Steinschneider teilen (den ich übrigens nicht kenne, wir stecken nicht in einer Verschwörungstheorie unter einer Decke).
c) Oder kommt es am Ende noch so, wie ich drüben bei Geograffitico geunkt habe, dass Grimes demnächst sagt, „April April“, ich wollte nur mal zeigen, wie man mit einer plausiblen Grundidee und ein paar Formeln eine ansonsten haltlose Geschichte in die Welt setzen kann? Dann wäre ihm der “Sokal-Hoax-Gedächtnis-Preis 2016“ sicher.
Um Einschätzungen der drei Alternativen wird gebeten, möglichst unter Verzicht auf die Heranziehung mathematischer Modelle, deren Betrachtung erneut zu diesen drei Alternativen führt.
———————
Nachtrag 8.2.2016:
Der Kommentar von “ajki” unten (#30) hat mich darauf aufmerksam gemacht, dass ich im Blogbeitrag mit starrem Blick auf das Modell meist unbedacht auch von “Verschwörungstheorien” spreche, wo es um “Verschwörungen” geht. Also: Grimes analysiert Verschwörungen, um damit zu zeigen, dass manche Verschwörungstheorien unglaubwürdig sind, weil sie als Verschwörungen nach seinem Modell schon aufgeflogen wären.
Nachtrag 7.3.2016:
Grimes hat eine Korrektur veröffentlicht:
https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0151003
Variante a) ist also richtig.




Kommentare (66)