Raster key 44: An encryption method from the Second World War and a message encrypted with it
The Raster Key 44 is a simple encryption method used by the Germans during World War II to replace the Enigma. Blog reader Allan Carstairs provided me with a challenge on this method.
Again and again I receive letters from readers which have something like the following wording: “I have invented an encryption method. A text encrypted with it reads: AKSH FKJA WFXS MAKJ. Can your readers crack it?”
Unfortunately, from experience, my readers are not very interested in such riddles. It gets a little more exciting when the encryption method used is known and my readers are only asked to guess the key. However, the matter is usually only interesting if no self-developed method was used, but a historically significant method. There are quite a number of excellent code breakers who are interested in such methods and also like to solve corresponding challenges.
I have published several such challenges myself, which has led to amazing successes and scientific publications. Here is a selection:
- Over ten years ago, I encrypted a text using the double cube method. George Lasry was able to solve it, which was widely reported in the media.
- My Playfair challenges have led to several records.
- My bigram challenges also led to records.
Allan Carstairs
A few weeks ago I had an exchange with blog reader Allan Carstairs, who runs a very interesting crypto challenge website, on this topic. It came up that the Raster Key 44 method from World War II is extremely interesting. We were not aware of a challenge for this cipher. Allan then created one.
But who is Allan Carstairs anyway? He wrote me the following about himself:
Allan Carstairs is a pseudonym I have adopted for the encrypted puzzle project. I am originally from Zimbabwe, Africa but have lived in other countries for the past twenty years. I originally became interested in codes and ciphers when I was about 9 years of age, in the mid 1970’s, when I bought myself a book on the subject, I think it may have been “Codes and Ciphers, Secret Writing Through The Ages” by John Laffin but I am not sure and I no longer have the book. This sparked my interest in modifying the ciphers detailed in the book to make them more secure.
Back in the 70’s and 80’s my peers were not interested in such things, so I lost interest after a few years. My interest was briefly rekindled when I read “The Code Book” by Simon Singh a few years ago. Then, in September last year I found a reference to the Vigenère cipher on the internet and realised the online interest. I decided I would try my hand again at improving the classical ciphers and as there seems to be more interest now I started the encrypted puzzle website. I am more interested in making classical ciphers secure using methods available to their original designers than breaking ciphers or in the modern digital encryption, about which I know nothing.
The raster key 44
The Raster 44 key is an encryption method introduced by the German military in 1944. All that was needed for this method was a form. A cipher tool or even a machine was not necessary.
The Raster key, like the double box, was intended as a replacement for the Enigma. If one was too expensive, too heavy or broken, which happened frequently, the Raster key was the intended alternative from 1944 on. The procedure is described, for example, in my book “Codebreakers versus Codemakers”. Further descriptions can be found here, here and here.
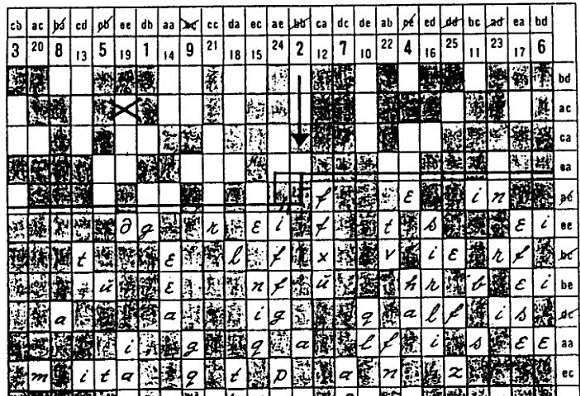
The Raster key 44 does not replace any letters, but only changes their order. The procedure thus belongs to the transposition ciphers. The form in question contains a matrix of 24 rows and 25 columns,
in which 15 fields per row are blackened.
Above each column there is a pair of letters (bigram) in which letters between a and e occur. As can be easily calculated, there are exactly 25 such bigrams, which means that one is available for each column. Each row is also assigned such a bigram, which is located at the end of the row.
Each field can be identified by a pair of bigrams. Thus, cdaa in the example stands for the fourth field in the fourth row. The distribution of the bigrams over the columns and rows is random and part of the key.
Above the 25 columns of the matrix, the numbers between 1 and 25 are additionally noted. Their order is also random and part of the key. The key of the method thus consists of four pieces of information: the location of the blackened fields, the distribution of the column bigrams, the distribution of the row bigrams, and the distribution of the numbers from 1 to 25 in the columns.
The encryptor enters his message line by line in the free fields of the form and then reads it out again column by column. The sender can choose the start field for entering the message. In the example the message THIS IS A SHORT TEST MESSAGE, and the start field is cdaa. Since
this is a redacted field (it is permissible to choose one), the text does not start until the next free field to the right of it, i.e. in bcaa.
The reading of the message starts in a column that the encryptor calculates in a method described below. For example, if this is the column with the number 7, then the sender notes its contents as the first part of the encrypted text (in the example, this is TI). As second
the column with the number 8 comes in the same way (Z), then the column with the number 9 (empty) and so on. After 25 it continues at 1.
In the example, this results in the encrypted message TIZIA EHUTT RSHID NISSN EREKC EECT.
The message is prefixed with the time, the number of letters, and the bigrams that mark the start field. However, the latter is not done in plain text, but with a substitution table that is not known to the codebreaker.
The column that is read first is determined by the sender using the time as well as the number of letters in the message. If the message is sent at 10:21 and it has 29 letters (as in the example), then the encryptor must add 1+0+2+1+2+9 (i.e. 15) to the column of the starting field. If the result is greater than 25, then 25 is subtracted. In the example, this results in 17+15-25=7. Thus, the readout starts in column 7.
The instructions to the encryptors during the Second World War provided for the insertion of meaningless terms (choice words) in a shorter message. The first and last choice words of a choice word block were indicated by doubling the este and last two terms, respectively (e.g., “HHAAUS … KATZZEE”).
The recipient can undo the encryption if he has the same form as the sender and the substitution table.
Thee Challenge
Allan Carstairs created the following challenge, which was created using grid key 44:
1244 ---- 198 ---- LGRJ KNGSR EWYTS TGURM AIWSW EDEHP AEIOH ETIRF RCDTA CSSID OEROK ASPEI LARNT FABWT EPLAD LNLOU EENOC TAIGY EAIRI ATRHU TSOAO ESNAR GEHST UIWSF WTSDT PUGKI SADHR EOSRR SDSEY HODEM RAOFW NBITI GTPEM NISBI PSERL CRVRL LCUHT TTESS FOOSH CREHS ELY
The plain text is written in English. There may be choice words in it. Can anyone solve this challenge?
If you want to add a comment, you need to add it to the German version here.
Follow @KlausSchmeh
Further reading: The Reihenschieber – A cold war encryption device
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/





Letzte Kommentare