Die Corona-Impfung schützt nicht zu 100 %, aber sie ist hochwirksam, vor allem, was schwere Verläufe und Tod angeht. Das lässt sich mit unterschiedlichen Methoden zeigen. Der „Goldstandard“ zur Bestimmung der Impfstoffwirksamkeit ist der Vergleich von Inzidenzraten zwischen Geimpften und Ungeimpften im RCT, dem randomisierten kontrollierten klinischen Versuch. Bei den Zulassungsstudien ist man so vorgegangen. Verglichen mit früheren, „bewährten“ Impfstoffen, hatte man dabei durchaus beachtliche Fallzahlen, aber RCTs haben naheliegenderweise ihre logistischen Grenzen und im Zulassungsverfahren kommen bei RCTs auch Einschränkungen hinzu, was den Einschluss bestimmter Personengruppen angeht, z.B. Kinder oder Schwangere.
Später, in der praktischen Anwendung, lassen sich, allerdings mit weniger strengen Studiendesigns, ebenfalls Wirksamkeitsberechnungen vornehmen. In einer inzwischen kaum mehr überschaubaren Zahl von Studien hat sich dabei die hohe Wirksamkeit der Corona-Impfung auch unter Alltagsbedingungen bestätigt, mit interessanten Befunden z.B. zum Vergleich der Wirksamkeit verschiedener Impfstoffe. Begrifflich wird dabei gelegentlich die „Impfstoffwirksamkeit“ von der „Impfeffektivität“ unterschieden, analog der gebräuchlichen Unterscheidung von efficacy und effectiveness. Im living e-book „Corona verstehen – evidenzbasiert“ wird darauf kurz eingegangen.
Die Impfeffektivität unter Alltagsbedingungen kann man je nach Art der verfügbaren Daten unterschiedlich berechnen. Das RKI schätzt die Impfeffektivität in seinen Wochenberichten nach der sog. “Screeningmethode nach Farrington“. Dabei werden nicht Inzidenzraten für Geimpfte und Ungeimpfte verglichen, sondern man stützt sich auf Angaben zur Impfquote bei Covid-19-Erkrankten relativ zur Impfquote in der Gesamtbevölkerung. Ein Schätzverfahren wie gesagt, keine ganz exakte Mathematik. Der SPIEGEL hat daran anlässlich einer Anpassung des Rechenverfahrens gerade eine ziemlich polemische Kritik veröffentlicht, aber wohl das Rechenverfahren nicht so ganz verstanden, weil mit dem Inzidenzvergleich von Geimpften und Ungeimpften argumentierend, der hier gar nicht zur Anwendung kommt und bei dem sich eine analoge Änderung des Verfahrens genau gegenteilig auswirken würde.
Im Wochenbericht vom 7.10.2021 kommt das RKI zu folgenden Ergebnissen:
• Impfeffektivität für den Zeitraum von der 5. bis 39. Kalenderwoche für die Altersgruppe 18-59 Jahre ca. 83 % und für die Altersgruppe ab 60 Jahren ca. 82%. Für den Zeitraum der letzten vier Wochen (36. bis 39. KW): für die Altersgruppe 18-59 Jahre ca. 80% und für die Altersgruppe ab 60 Jahren ca. 77%.
• Schutz vor Hospitalisierung: ca. 92% (18-59 J.) bzw. ca. 88% (ab 60 J.)
• Schutz vor Behandlung auf Intensivstation: ca. 95% (18-59 J.) bzw. ca. 93% (ab 60 J.)
• Schutz vor Tod: ca. 99% (18-59 J.) bzw. ca. 90% (ab 60 J.)
Wie gesagt: Die Corona-Impfung ist hochwirksam, auch gegen die derzeit dominante Delta-Mutante. Demgegenüber wird im Internet allerdings immer wieder einmal darauf verwiesen, dass es einen großen Anteil an Sterbefällen unter den Geimpften gibt. Klar ist, dass der Anteil der Geimpften unter den Gestorbenen notwendigerweise zunehmen muss, wenn die Impfquote steigt. Trivialerweise könnte es, wenn alle geimpft wären, nur noch geimpfte Gestorbene geben. Aber wenn unter den Geimpften auch noch die Sterberate höher ist als unter den Ungeimpften, dann kann das in der Tat irritieren.
In einem kleinen Methodensplitter, der in Heft 10/2021 der Zeitschrift „Gesundheitswesen“ erscheinen soll, wird kurz erläutert, wie es dazu kommen kann. In Bayern lag Mitte Juli 2021 die Fallsterblichkeit („Case Fatality Rate“, CFR) aller Coronafälle kumulativ bei 2,4 %, die der unvollständig Geimpften bei 3,4 %, die der vollständig Geimpften bei 4,3 %. Erhöht also die Impfung das Sterberisiko, wie manche daraus messerscharf schließen?
Wie diese Zahlen zu den guten Angaben zur Wirksamkeit der Impfung passen, zeigt sich, wenn man die CFR nach Alter differenziert, also altersspezifische Sterberaten bildet. Dann sieht man, dass sie in jeder einzelnen Altersgruppe bei den vollständig Geimpften deutlich niedriger ist als bei den unvollständig Geimpften und hier wiederum niedriger als bei allen Infizierten (die Ausnahme in der Altersgruppe 30-49 ist zufallsbedingt aufgrund sehr kleiner Fallzahlen).
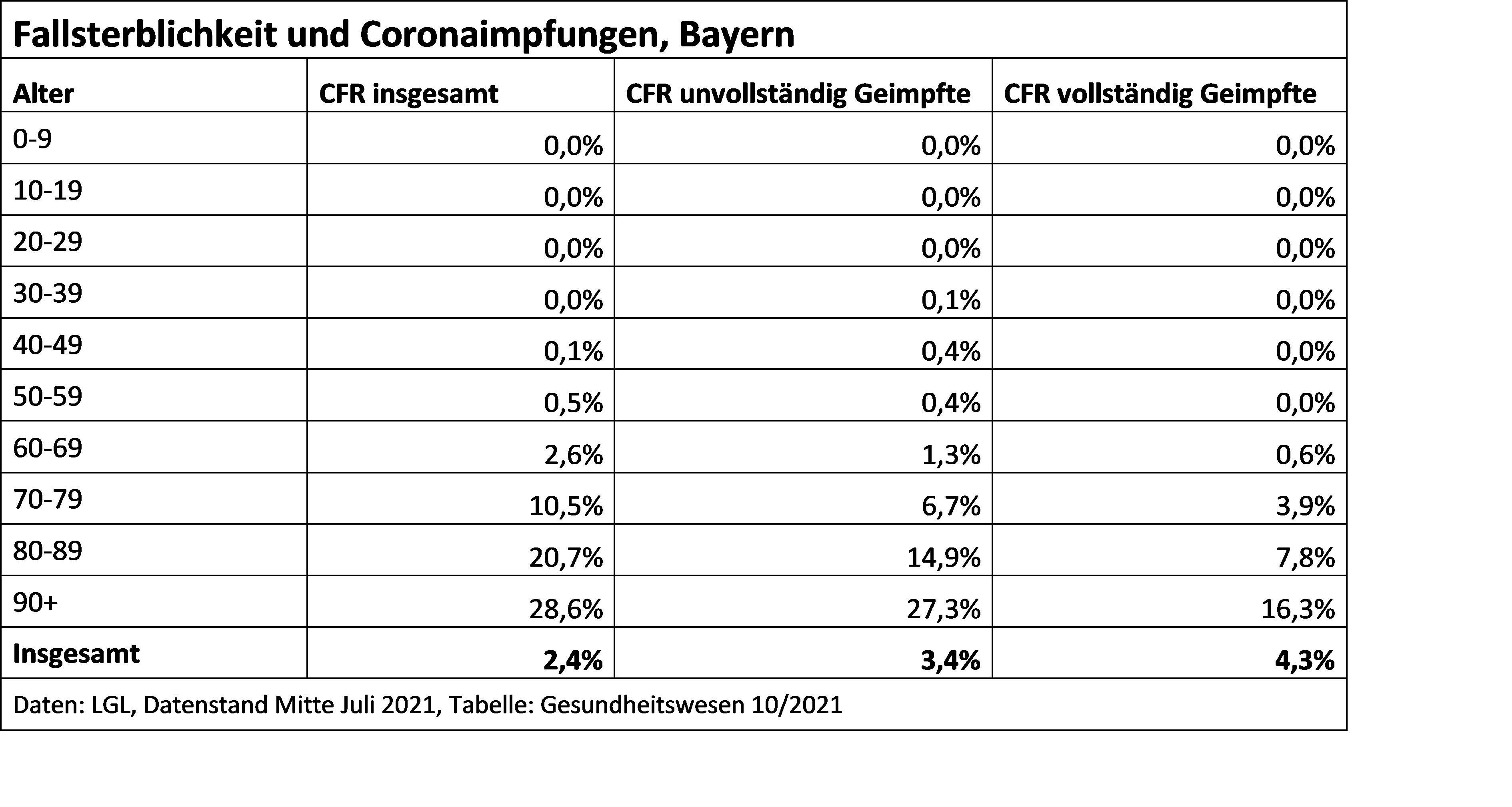
Was man hier sieht, ist das berühmte „Simpson-Paradoxon“. Die ungewichtete Gesamtrate von 4,3 % Gestorbenen unter den vollständig Geimpften ist am höchsten, weil hier viele Hochaltrige mit höheren Sterberaten enthalten sind. Das Simpson-Paradoxon verschwindet, wenn die Gesamtraten der drei Gruppen altersstandardisiert werden, was bei Ratenvergleichen zwischen Gruppen mit unterschiedlichem Altersaufbau und altersabhängigem Outcome immer sinnvoll ist. Auf die Bevölkerung Bayerns 2019 standardisiert waren es 2,8 %, 2,0 % und 1,0%.




Kommentare (60)