StartseiteCipherbrain

LCS35-Kryptogramm: Ein Verschlüsselungsrätsel, dessen Lösung 35 Jahre dauert

Von / 12. Juli 2014 / 21 Kommentare
Mehr

1999 veröffentlichte der Kryptologe Ron Rivest einen verschlüsselten Text. Um ihn zu dechiffrieren, muss man eine kurze mathematische Gleichung lösen. Das ist relativ einfach, dauert aber extrem lang. Bisher hat es niemand geschafft.

Wissen Sie, was ein Time-Lock-Puzzle ist? Dabei handelt es sich um ein (mathematisches) Rätsel, für dessen Lösung man sehr viel Zeit benötigt. Time-Lock-Puzzles sind sehr hilfreich in der Kryptologie. Wenn man die Lösung eines solchen Rätsels als Schlüssel verwendet, dann ergibt sich eine interessante Situation: Wer an den Schlüssel herankommen (und damit einen bestimmten verschlüsselten Text entschlüsseln) will, braucht dafür sehr lange. Dafür gibt es zahlreiche Anwendungen:

  • Ein Bieter bei einer Auktion will sein Gebot so verschlüsseln, dass es erst nach Ablauf der Ausschreibungsfrist entschlüsselt werden kann.
  • Ein Tagebuch-Autor will seine Aufzeichnungen so verschlüsseln, dass sie erst für kommende Generationen entschlüsselbar sind.
  • Ein Hellseher, der bereits jetzt weiß, wie das morgige WM-Finale zwischen Deutschland und Argentinien ausgeht, will sein Wissen beweisen, ohne durch eine Vorab-Veröffentlichung irgendwelche Wettbüros zu ruinieren.
  • Eine Polizeibehörde soll die Möglichkeit haben, verschlüsselte E-Mails mitzulesen – aber nur mit zeitlichem Abstand und wenn sie einen gewissen Aufwand investiert.
  • In einem Währungssystem soll jeder die Möglichkeit haben, Geld zu “drucken” – trotzdem soll die Geldmenge beschränkt bleiben (nach diesem Prinzip funktioniert BitCoin).

Die Idee der Time-Lock-Puzzles stammt aus den neunziger Jahren. Hier gibt es eine Arbeit dazu.

1999 stellte der Kryptologe Ron Rivest ein Time-Lock-Puzzle (LCS35-Kryptogramm) vor. Es basiert auf einer einfachen mathematischen Formel:

LCS-35-bar

Die Werte von t und n sind festgelegt (siehe Ende des Artikels). Es geht also darum, den Wert von w zu finden (“mod n” steht für den Rest, der beim Teilen entsteht). Der Haken bei der Sache: t und n sind sehr große Zahlen. Die einzige bekannte Lösungsmethode ist sehr aufwendig und lässt sich nicht parallelisieren.

Banner-Kryptografie

Rivest schätzte, dass es 35 Jahre dauern würde, um das Rätsel zu lösen – sofern stets ein aktuelles Computer-Modell eingesetzt wird. 15 Jahre Später dürfte es deutlich schneller gehen (kann mal jemand ausrechnen, von welchem Zeitraum man bei Anwendung des Mooreschen Gesetzes ausgehen kann?). Wer nun anfangen will, sollte beachten: Passiert bei der ganzen Rechnerei auch nur ein einziger Fehler, dann kommt am Ende ein falsches Ergebnis heraus.

t = 79685186856218

n = 631446608307288889379935712613129233236329881833084137558899
077270195712892488554730844605575320651361834662884894808866
350036848039658817136198766052189726781016228055747539383830
826175971321892666861177695452639157012069093997368008972127
446466642331918780683055206795125307008202024124623398241073
775370512734449416950118097524189066796385875485631980550727
370990439711973361466670154390536015254337398252457931357531
765364633198906465140213398526580034199190398219284471021246
488745938885358207031808428902320971090703239693491996277899
532332018406452247646396635593736700936921275809208629319872
7008292431243681

Stichworte: ,
Mehr

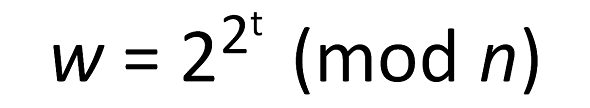
Kommentare (21)

  1. #1 DeLuRo
    12. Juli 2014

    Der Link Hier gibt es eine Arbeit dazu funktioniert leider nicht korrekt — http: // fehlt.

    • #2 Klaus Schmeh
      12. Juli 2014

      Danke, wird korrigiert.

  2. #3 rolak
    12. Juli 2014

    bei Anwendung des Mooreschen Gesetzes

    kommt man keinen Schritt weiter, da es die Komplexität der IC-Technik betrifft, nicht jedoch die Rechenleistung der damit gebauten Computer.

    Ansonsten, unter dem analogen Postulat, daß sich jedes Jahr die erreichbare Geschwindigkeit bei der Lösung just diesen Problemes verdoppelt, diese Entwicklung gleichmäßig verläuft und instantan umgesetzt wird, gehts wie beim Tempo: s(T)=35km, v0=1/35 km/y, v(t)=v_0 2^t => s(T)=\int_0^T t v_0 2^t dt oder bei ca 7,2 Jahren ist das Ende nahe.

    • #4 Klaus Schmeh
      12. Juli 2014

      Interessant, in gut sieben Jahren könnte man das Rätsel also lösen – wenn kein Fehler passiert.

  3. #5 hugo
    12. Juli 2014

    bzgl Mooreschem Gesetz:
    Rivest hat das doch in seine Schätzung von 35 Jahren schon mit einbezogen (“…the computer being replaced every year by
    the next fastest model available.”).
    Und selbst wenn nicht: rolaks Rechnung ist an zwei Stellen fehlerhaft: Wenn man s(T)=35 km (warum auch immer km) setzt, sollte v0 doch gleich 1km/y sein (für v(t)=v0=const. muss ja T=35y rauskommen). Und das t im Integral ist auch nicht so sinnvoll…

    • #6 rolak
      12. Juli 2014

      1km/y

      ärgks, doppelt runtergerechnet

      warum auch immer km

      Weils auf die üblichere und gewohntere Frage “wann ist bei der und der Geschwindigkeit die Strecke durchfahren” umgebaut wurde.

      t im Integral ist auch nicht so sinnvoll

      Nicht? Bisher war mir so als würde s=t*v gelten.

      Simpler wirds bei jährlicher Ersetzung des abgenudelten Altrechners, da werden im Jahre J nach dem Start \frac{2^J}{35} des Problems gelöst, an den Jahresenden sind also 1, 3, 7, 15, 31 Fünfundreißigstel erledigt und ca Karneval des sechsten Jahres ist alles vorbei. Der Aschermittwochs-Effekt.

  4. #7 DeLuRo
    12. Juli 2014

    @hugo, rolak: Das Argument von hugo ist richtig, Rivest nahm in seinem Text explizit an, dass der Rechner jedes Jahr durch das schnellste Modell ersetzt würde. Dabei setzte er voraus, dass das Moor’sche Gesetz bis zum Jahr 2012 linear angewendet werden könnte, und danach sei bis 2034 noch eine Verfünffachung der Geschwindigkeit möglich. Insgesamt also ein Faktor 64 oder 65, den er in seine Schätzung mit einbezog. Nebenbedingung ist, dass der Algorithmus weiterhin nicht parallelisierbar sein wird, und dass n als Produkt zweier großer Primzahlen nicht effektiver (als bisher) faktorisierbar ist.

    • #8 rolak
      12. Juli 2014

      Argument von hugo ist richtig

      Klar, doch Klaus’ Frage ließ trotz des ‘stets den..’ darauf schließen, daß ‘Rechner einschalten bis er fertig ist’ die aktuelle Variante war. Zugegeben, das paper gelesen habe ich nicht, warum sollte ich. Nur um die Interpretation Richtung Sinnhaftigkeit der Frage zu verifizieren?

      Letztlich sehe ich Möglichkeiten sowohl im SW- (oder hat doch schon jmd die Nicht-Parallelisierbarkeit gezeigt?) als auch im HW-Bereich.

  5. #9 hugo
    12. Juli 2014

    @rolak:
    s = \int v dt, nicht \int t v dt

    • #10 rolak
      12. Juli 2014

      -.- durchgemachte Nacht

  6. #11 joe
    Berlin
    12. Juli 2014

    Hallo,
    also wenn ich in der Schule doch mal richtig aufgepasst habe kann man die Potenzrechnung “vereinfachen”:

    2 ^(2*t) (MOD n)

    It es richtig das n keine Primzahl bzw. ungerade Zahl ist?

    Jörg

  7. #12 Klaus Schmeh
    12. Juli 2014

    >Rivest hat das Mooresche Gesetz doch in seine Schätzung
    >von 35 Jahren schon mit einbezogen
    Stimmt. Er hat von 1999 an gerechnet. Wenn man 2014 anfangen würde, müsste es deutlich schneller gehen (die Aufgabe an sich hat sich ja nicht geändert).

  8. #13 DeLuRo
    12. Juli 2014

    @joe: Lies am besten den Text von Rivest aus dem 3. Link; er ist nicht zu lang, und das Programm kann man weglassen.
    Die Gleichung kann man etwas umformen, siehe Text, aber deine Zeile sieht mir nicht richtig aus. 2^t ist nicht dasselbe wie 2 * t , das Potenzieren bindet stärker, oder man sollte gleich 2 ^ (2^t) schreiben. Etwas anderes mag für das Ergebnis der Anwendung des Modulo gelten. — n ist nach Rivest das Produkt zweier großer Primzahlen und damit ungerade.

  9. #14 DeLuRo
    12. Juli 2014

    @myself: bzw. das Argument beim Potenzieren ist, dass der Operator in dieser Schreibweise rechtsassoziativ ist, also das “Innere” zuerst.

    • #15 Klaus Schmeh
      12. Juli 2014

      Ja, das muss so sein, sonst ist der Exponent zu klein, um die Aufgabe schwierig zu machen. Außerdem könnte man andernfalls statt (2^2)^t ja gleich “4^t” schreiben.

  10. #16 sfa
    13. Juli 2014

    also, zumindest “mod n” lässt sich parallisieren. cpu1 div x, cpu2 div x+1, zurück zum koordinator und schaun ob mod erfüllt

    • #17 Klaus Schmeh
      13. Juli 2014

      Das würde sicherlich eine Verkürzung pro Arbeitsschritt bringen, aber die Anzahl der Arbeitschritte bliebe gleich. Oder liege ich falsch?

  11. #18 DeLuRo
    13. Juli 2014

    @sfa: Ich verstehe nicht, wohin “schaun ob mod erfüllt ist” führen soll, und wieso sollen a div x, a div (x+1), … berechnet werden?
    Der Modulo-Operator berechnet einen Rest bei Division, das funktioniert immer, auch wenn der Rest 0 sein sollte (was in diesem Beispiel unsinnig wäre).

    Die Aufgabe ist doch folgende: t ist eine Zahl in der Größenordnung 10^14, man kann diese Zahl noch mit 47 Bit plus Vorzeichen darstellen. Dann wird 2^t gebildet, binär eine 1 mit t Nullen hinten dran. Würde man diese Zahl mit einem Bit je Datenbyte speichern, hätte sie alleine schon eine Darstellung von 72 Terabyte Daten. Und dann soll noch 2^(2^t) gebildet werden, eine Zahl mit Stellen größer als die (vermutete) Anzahl von Kernteilchen im Universum. Außerdem hat n 616 dezimale bzw. 2048 binäre Stellen.

    Die Aufgabe verlangt nun nichts anderes, als dass man 2^(2^t) bildet, diese dann durch n teilt und den Rest der Division berechnet (und diesen dann mit einem Kryptotext ver-xodert). Das Dumme ist nur, dass man die erste Zahl nicht real im Rechner darstellen kann, auch nicht logarithmisch, und man also ein Ersatzverfahren benötigt. Aufgrund einiger Gesetze für Division und Modulo (in Restklassenringen) ergibt sich: man berechnet w(0) = 2, und für i=1,…,t : w(i) = Mod( w(i-1) ^2, n). w(t) ist dann das gesuchte w(t).

    Der Knackpunkt der Parallelisierung ist nun, dass für jede Berechnung des w(i) vorher das w(i-1) bekannt sein muss. Das ist gemeint mit einem “intrinsisch seriellen Problem”. Abgesehen davon kann w(i) nie größer als n^2 sein und es reichen daher 4096 Bit (128 Dword) für die Arithmetik aus; das kann mit Routinen für Langinteger erreicht werden. Diese können zwar intern durch Parallelisierung beschleunigt werden, aber nicht durch CPU-Threads (das würde eher bremsen). Es bleiben jedoch immer ca. 10^14 Iterationen für w(i).

  12. #19 DeLuRo
    13. Juli 2014

    @myself: “…w(t) ist dann das gesuchte w der linken Seite”.

    Noch eine Überlegung: bei 10^14 Iterationen muss ein Rechner im Schnitt erstaunliche gute 700.000 pro Sekunde schaffen, um die 35 Jahre zu erreichen.

  13. #20 DeLuRo
    16. Juli 2014

    Falls es niemandem aufgefallen ist: ich habe mich verrechnet, und es sind nur 72.000 Iterationen pro Sekunde (im langjährigen Schnitt). Heutige Rechner können das wohl mit nur einem Kern. Ansonsten wäre die Geschichte auch schon in 3,5 Jahren gegessen gewesen.

  14. #21 Verschlüsselung auf Zeit | Lehrerzimmer
    9. August 2014

    […] ein paar Wochen stellte Klaus Schmeh in Klausis Krypto Kolumne ein Time-Lock-Verschlüsselungsverfahren vor. Um das Prinzip richtig zu begreifen, habe ich das alles nachprogrammiert, und wenn ich mir so viel […]