StartseiteCipherbrain

Fleissner challenge: can this cryptogram be broken?

Von / 13. Januar 2017 / 19 Kommentare
Mehr

The Fleissner grille is one of the most popular encryption tools. In spite of its popularity, surprisingly little has been published about deciphering a Fleissner grille. I wonder if a reader can break the Fleissner challenge I am going to present today.

Even if you’re not very familiar with cryptography, you might have heard of the Fleissner grille. The Fleissner grille is named for Edouard Fleissner von Wostrowitz (1825–1888), who described it in one of his publications. However, this method had long been known before.

 

The Fleissner grille

A Fleissner grille is a square stencil looking like this:

Fleissner-Grille

Fleissner grilles exist in different sizes. The one above (provided to me by Andreas Önnerfors) is based on a 12×12 matrix. The following grille (from the Heinz Nixdorf MuseumsForum) is a 15×15 version:

Fleissner-Paderborn

 

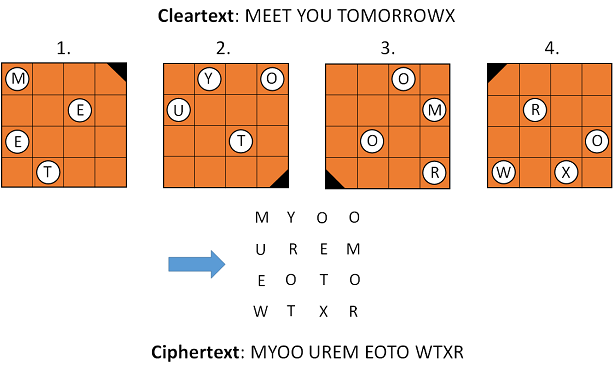
How it works

Here’s how a Fleissner grille works (the stencil is used four times, each step is followd by a 90 degree turn):

Fleissner-Explanantion

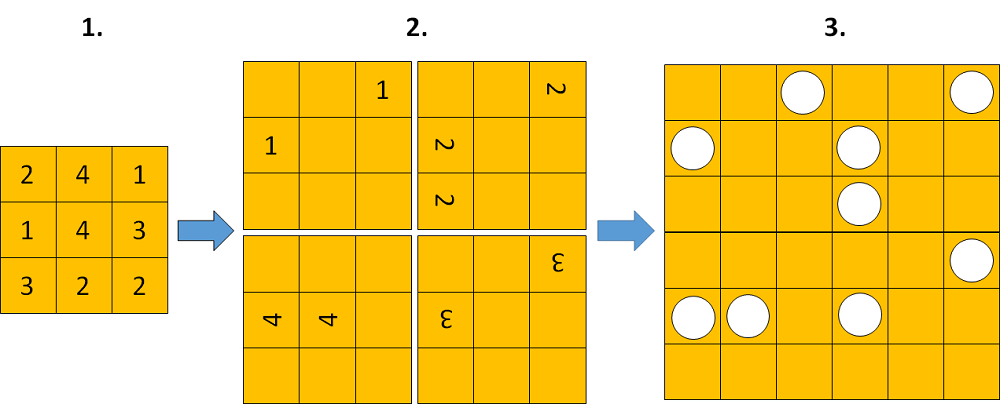
A Fleissner encryption represents a transposition cipher. This means that no letter substitution takes place. Instead, the order of the letters is changed. To construct a Fleissner grille you can proceed as follows (start with a square matrix and fill it with numbers from 1 to 4 at random):

Fleissner-Construction

 

A genuine Fleissner cryptogram

The following encrypted message created with a Fleissner grille was found (and broken) by my Dutch friend Karl de Leeuw in an archive in the Netherlands (see here for details):

Fleissner-Leeuw

 

A Fleissner challenge

Karl de Leeuw broke the Fleissner cryptogram shown above with a marvelous side channel attack. This attack only works, when the user is sloppy in writing down the ciphertext. Of course, there are also cryptoanalytical methods to solve a Fleissner encryption. However, not much has been published about this. The only substantial treatise about breaking Fleissner encipherments I am aware of is a chapter in the book Cryptanalysis by Helen Fouché Gaines (published in the 1950s). Gaines shows how a 6×6 Fleissner message is broken based on the (correct) assumption that the word VIADUCT appears in it. It should be clear that it gets much harder if we deal with a larger matrix and no cleartext word is known.

When Gaines wrote her book, computers were almost non-existent. As this has changed, it would be interesting to know how well a Fleissner cryptogram can be attacked with computer support. To stimulate research in this field I have created a Fleissner challenge. The following ciphertext was created with a 20×20 Fleissner grille from an English cleartext:

EAPTISUZLANEDETHSPNF
EIORDEMAARNNAROORFTL
AETLMLOIFHATOEUDMVNE
OXNPBAOEDOIGTRANEEIU
XPNPOURNTASEOMMWDHAN
IANHTNEIEODNSOTOTETD
MONENANPRRIOLAOGNELN
INATCFIVOREATDNIEDDA
UHIIEURININGTTEDNSTN
ATGHPEESAOAEISETDRMM
YANTSOEITESYTEVTTACH
BNINCALEHUCHTHALLHLG
OIKWESOEHRNGREERRRME
SAAMHIBEIDMNSAINARLI
DTESGINTETACIARHLYLM
ESESRUUISINEADSRANOE
COSWOEAUETJPOERNSDTW
BYEPFNINGHERHIVNTOSE
MNTBERAEOLUNNANSYIIX
TPOUTYPFIEOWVULEACRA

Can a reader break this cryptogram? A Hill Climbing algorithm might be a good candidate to try. Hill Climbing means (in this case): a Fleissner grille is constructed at random and used to decrypt the cipher text. The result is fed to a function that rates the correctness of the letter sequence (for instance, based on whether the bigram frequencies ressemble the ones of English text). Then the grille is changed slightly, and again the ciphertext is decrypted and rated. If the rating is better now, the current grille will be kept, otherwise the previous one is reloaded. Again, the grille is changed slightly, used for decryption and the result is rated, and so on. This procedure is carried on, until the rating doesn’t improve any more. If we are lucky, this maximum rating indicates that we have found the correct grille.

Codebreakers like George Lasry, Nils Kopal, Jim Gillogly and Dan Girard have been very successful with Hill Climbing. Maybe this technique will solve the Fleissner challenge, too.

Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/

Further reading: How to Use a Rubik’s Cube for Encryption

Stichworte:
Mehr

Kommentare (19)

  1. #1 Thomas
    13. Januar 2017

    Also Friedman wrote about breaking revolving grilles in general:
    https://archive.org/stream/41761079080022#page/n50

  2. #2 Norbert
    Berlin
    14. Januar 2017

    @Thomas: Danke für den Hinweis und Link, es ist doch immer wieder erstaunlich, wieviele Felder Friedman schon beackert hat!

    Ausgehend von Friedmans Prinzipien, würde mir ein Algorithmus vorschweben, der sich von Hill Climbing unterscheidet. Der Fachbegriff ist mir unklar, ich nenne das für mich meistens “Vorwärtshangeln”. Leider fehlt mir gegenwärtig die Zeit, die Idee in die Tat umzusetzen. Hier eine Kurzbeschreibung:

    Ich definiere zunächst diejenige Position der Schablone, bei der das Zeichen oben links sichtbar ist, als Position 1. Ich weiß somit, dass der 100 Buchstaben umfassende Textabschnitt für Position 1 mit “E” beginnt. Gleichzeit weiß ich, dass der Textabschnitt für Position 3 (Schablone um 180° gedreht) mit “A” (dem Buchstaben unten rechts) aufhört.

    Das Programm soll in einem ersten Schritt alle Möglichkeiten für die ersten vier Buchstaben in Position 1 durchgehen, es ergibt sich dabei (der erste Buchstabe steht ja schon fest) ein Klartext-Tetragramm “E???”, aber gleichzeitig ein weiteres Tetragramm für die um 180° gedrehte Schablone: “???A”. Die statistischen Häufigkeiten dieser beiden Tetragramme für die englische Sprache sind zu multiplizieren, um sozusagen die Wahrscheinlichkeit zu erhalten, dass die gewählte Position richtig geraten ist (wenn man wie üblich mit den Logarithmen der Häufigkeiten arbeitet, sind die beiden Werte zu addieren).

    Das sind ca. 10 Millionen Kombinationen, die das Programm im ersten Schritt bearbeitet. Es behält davon eine gewisse Anzahl, z. B. die 10000 Möglichkeiten mit den besten Wahrscheinlichkeitswerten, im Speicher, alle anderen Kandidaten werden verworfen. Nun hangelt man sich vorwärts: Für jedes der 10000 Tetragramme untersucht man alle Möglichkeiten für einen fünften Buchstaben und ermittelt wieder die Wahrscheinlichkeitswerte, die sich daraus ergeben, dass neben dem nun entstandenen Pentagramm ein weiteres für die um 180° gedrehte Schablone feststeht. Wieder werden die 10000 besten Kandidaten behalten, der Rest verworfen, und so geht es weiter, bis man bei hundert Zeichen angekommen ist. Unterwegs muss darauf geachtet werden, dass die Kandidaten korrekte Schablonen ergeben können (entspricht Friedmans “principle of exclusion”), das verkleinert die Zahl der zu untersuchenden Möglichkeiten und verringert hoffentlich auch die Gefahr, dass sich Bruchstücke von Schablonenposition 2, 3 und 4, die vielleicht zufällig an irgendeinem Punkt gut passen, in die Suche hineinmischen und alles durcheinander bringen (die vermutlich größte Gefahr bei meinem Ansatz).

    Mit etwas Glück findet man am Ende korrekte Klartextviertel (und die richtige Schablone) ganz weit oben in der Kandidatenliste.

  3. #3 Klaus Schmeh
    14. Januar 2017

    @Norbert: Das ist ein interessanter Ansatz. Die wichtigste Frage ist wohl, ob man aus den vielen Verästelungen, die selbst jeweils weitere Verästelungen nach sich ziehen, am Ende den richtigen Ast herausfiltern kann. Es könnte funktionieren.

  4. #4 Klaus Schmeh
    14. Januar 2017

    Jim Gillogly via Facebook:
    My program struggles with large squares, and isn’t reliable much past the ACA guideline of 12×12 for what we call “Grille” (aka Turning Grille). I didn’t know anything about the history of it, and was pleased to see some background in the article. I let it go overnight, and although it came up with suspiciously coherent phrases like “[he?]unitedstatesarmy” and [posedmany?]technicalchall” it had less coherent suggestions like “”…fated on..export..need someone…” and “saint carlie droe sword.figh..” and “outjest befingers meant…”. I tuned the program for the ACA guideline, though, so it’s possible that other square manipulations could extend its range somewhat.

  5. #5 Klaus Schmeh
    14. Januar 2017

    Jim Gillogly via Facebook:
    Two more notes: first, the grille can just as easily be rotated widdershins rather than the usual deasil shown above. Also, a rough estimate of increasing difficulty may be the size of the key space, which is two bits each for each cell in the key quadrant – 2×36=72 bits for the 12×12 ACA version, or 2×100=200 bits for the challenge above. Naturally this doesn’t give the same strength as a 200-bit modern computer cipher, but does suggest that larger squares may be substantially harder than smaller ones.

  6. #6 Martin
    Bern/Schweiz
    15. Januar 2017

    ^
    EAPTISUZLA|NEDETHSPNF
    EIORDEMAAR|NNAROORFTL
    AETLMLOIFH|ATOEUDMVNE
    OXNPBAOEDO|IGTRANEEIU
    XPNPOURNTA|SEOMMWDHAN
    IANHTNEIEO|DNSOTOTETD
    MONENANPRR|IOLAOGNELN
    INATCFIVOR|EATDNIEDDA
    UHIIEURINI|NGTTEDNSTN
    ATGHPEESAO|AEISETDRMM
    ———-+————>
    YANTSOEITE|SYTEVTTACH
    BNINCALEHU|CHTHALLHLG
    OIKWESOEHR|NGREERRRME
    SAAMHIBEID|MNSAINARLI
    DTESGINTET|ACIARHLYLM
    ESESRUUISI|NEADSRANOE
    COSWOEAUET|JPOERNSDTW
    BYEPFNINGH|ERHIVNTOSE
    MNTBERAEOL|UNNANSYIIX
    TPOUTYPFIE|OWVULEACRA

    The position of the A above and right of the coordinate center would be (1,1), the E next to it (1,2) etc.
    If the grille has a hole at (1,2) then by turning clockwise 90 degree we get (1,-2) the C, again turing (-2,1) the T and again (-1,2) the I.
    (Ignoring the x and y value 0 as turning the grille/hole is simpler this way)
    Initializing the grille would be: for each point in the upper right quadrant randomly choose it or one of its other 3 possiblities e.g.:
    (-1,-1), (2,-1), (1,3), (1,-4), (1,-5), (1,-6), (-1,-7), …
    With this init vector hill climb can be started. To vary the vector during hill climb I would rotate each hole in its four positions.

    I don’t think Norbert’s idea works as it is not sure where the first letter is. Imagine all the holes are in the upper right quadrant (I now then there is no encryption)
    so the E in the upper left corner would come in the last 90 degree turn.

  7. #7 Armin
    16. Januar 2017

    The Grille contains the following plaintext:

    PLANS FOR MANNED MOON EXPEDITIONS ORIGINATED DURING THE EISENHOWER ERA IN AN ARTICLE SERIES WERNHER VON BRAUN POPULARIZED THE IDEA OF A MOON EXPEDITION A MANNED MOONLANDING POSED MANY TECHNICAL CHALLENGES BESIDES GUIDANCE AND WEIGHT MANAGEMENT ATMOSPHERIC REENTRY WITHOUT OVERHEATING WAS A MAJOR HURDLE AFTER THE SOVIET UNIONS LAUNCH OF THE SPUTNIK SATELLITE VON BRAUN PROMOTED A PLAN FOR THE UNITED STATES ARMY TO ESTABLISH A MILITARY LUNAR OUTPOST BY NINETEEN SIXTY FIVE

    This grid would well be solvable with a Hill climber. But there is one difficulty: At the third rotation of the mask, the plaintext is not entered left to right from top to bottom in the empty spaces, but vertically from right to left, top to bottom. Once I realized this, the Hill climber did the rest.

  8. #8 Norbert
    16. Januar 2017

    @Armin: Congratulations!
    In the meantime, I managed to code my approach. While it worked fine for some 8×8 test squares, it failed with the 20×20 challenge cipher. (At least, it revealed similar fragments of the plaintext as did Jim’s program: “technical challenge[s]” and “for the United States”).
    So the superiority of the hill climbing approach is proven! I think one reason might be that a hill climber can score the whole text, with all rotations of the mask, from the beginning, whereas my program stays a long time limited to one rotation and its 180 degree counterpart.

  9. #9 Marc
    16. Januar 2017

    @Armin
    Super, trotz “eingebautem Fehler” (ist natürlich Absicht vom Klaus gewesen), gelöst. Darf ich fragen, wie lange dein Hill-Climber für diese Aufgabe so ca. im Schnitt benötigt ?

  10. #10 Nils
    Kassel
    16. Januar 2017

    Gratulations Armin… i changed my hillclimber the way you said and suddenly saw EISENHOWER… I am curious to see what will come out at the end. Thus, i spent the whole weekend on optimizing my program in the wrong direction. Nevertheless, nice that you solved that Armin 😉

    @Klaus: I really like that you create such challenges… BUT: It would be nice if you stay with Kerkhoff 😛
    Working on data with the wrong assumptions do not help us to improve our algorithms… in the worst case, they make them worse 🙂

    @Armin: Which kind of cost-function do you use?

  11. #11 Tony
    16. Januar 2017

    Well done Armin – I was having a go at this with pencil and paper and found the word ‘challenge’ which was confirmed by rotating 180 degrees which produced ‘for the’ – I was still struggling when I saw your solution – again well done.

  12. #12 Klaus Schmeh
    16. Januar 2017

    Thank you Armin, great job!!!

    >At the third rotation of the mask, the plaintext is not
    >entered left to right from top to bottom in the empty
    >spaces, but vertically from right to left, top to bottom.
    You’re right, I’m terribly sorry. It was not my intention to trick somebody. I simply forgot to turn the grill (on my Powerpoint slide) before I filled in the third part. I corrected this mistake immediately by turning the grille and turning the grouped letters. Then I ungrouped the letters and turned them again. It seemed like a good idea, but I didn’t realise that the order of the letters was wrong now.

    >I really like that you create such challenges…
    >BUT: It would be nice if you stay with Kerkhoff
    Yes, sorry, I will be more careful next time.

  13. #13 Klaus Schmeh
    16. Januar 2017

    @Jim Gillogly:
    >“[he?]unitedstatesarmy” and >[posedmany?]technicalchall”
    Your guesses were correct.

  14. #14 Thomas
    17. Januar 2017

    @Armin: Well done! Is your solution based on Friedman’s principles?

    @Klaus: So you didn’t use paper and scissors 😉

  15. #15 Armin
    17. Januar 2017

    @Thomas: The Hill climber doesn’t directly make use of Friedman’s principles. But I used the fact that known plaintext fragments give more plaintext fragments, when the stencil is rotated by 180°, to identify correct holes and thus reduce the search space for the Hill climber.

  16. #16 Gillogly
    18. Januar 2017

    @Armin: I was wondering whether my hill-climber would be more effective if it used that 180-degree observation to work on diagonally opposite quadrants, at first ignoring the effects on the other two quadrants. I’d thought about implementing that when you posted your solution, so I haven’t gotten around to trying it. In the event, I guess it could have done well on rotations 1 and 3, but would still have been confused by the different direction for rotation 4.

  17. #17 Hendrik
    19. Januar 2017

    I also managed to solve the grille. I used a hill climbing algorithm with quadgram frequencies to rate the acurateness of the decrypted text.
    The algo starts with a random grille and will search for the best solution possible by only changing one cell. If this best solution is better than the previous one it will go on with it (apply the change) and start again the search for the best solution. If not, it will apply a random two-cell-change and restart. I used the information from Armin that in the last move the grille is not readout as expected. Not sure if it would work out well without that hint. Maybe I will test it.
    If anyone is interested in the Java source code. Let me know and I will share.

    @Klaus: Thanks for this challenge. It was a lot of fun 🙂

  18. #18 BE
    19. Januar 2017

    Hello Hendrik,
    do you know the e-learning program Java-CrypTool (JCT)? (see https://www.cryptool.org/en/jcryptool)
    It has a visualization of how the Grille cipher works, but no analysis. It would be great if you could send me your Java code so maybe I find a student to integrate it in JCT. Or maybe you want to do so by yourself?
    Best regards, Bernhard

  19. #19 Hendrik
    19. Januar 2017

    Hello Bernhard,
    I didn’t know JCT. Sounds interesting. I just recently stumbled across Klaus blog and was fascinated. This was my first try on decrypting.
    Feel free to download the Java code here: https://www.somany.de/fleissnergrille/src.zip
    (It is far away from perfect. A lot is hardcoded. This was for fun rather than “good coding” 😉 Anyway, it works..)

    Best regards,
    Hendrik