A Rubik’s Cube can be used to implement a low-tech encryption method. But is it secure? Here’s a challenge for my readers to solve.
In a Cryptologia publication from 1992, Douglas W. Mitchell proposed an interesting cipher that does not require computer support: encryption with a Rubik’s Cube.
The algorithm
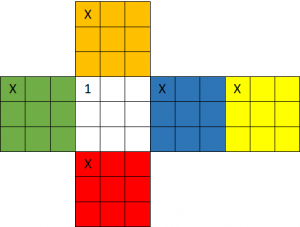
To use Mitchell’s cube encryption algorithm, the surface of the cube should be coated so that it can be written on. The colors on the cube faces are irrelevant.
To begin with, write the numeral “1” on the upper left square of one of the cube faces. Write “2” on an arbitrarily chosen square of any other cube face, write “3” on any square of any other cube face, and so on.
Then fill in a 48 letter plaintext on the remaining 48 squares of the cube. The first eight letters are written on cube face “1”, letters 9 to 16 on cube face “2”, letters 17 to 24 on face “3” and so on. Always start writing in the upper left cube of the face. As an example, I took the cleartext “ABCDEFGHIJKLMNOPQRSTUVWXabcdefghijklmnopqrstuvwx”.
For encryption and decryption to work properly, it must be defined, which corner is considered as the upper left one (this is only clear for the front face). I used the following scheme:
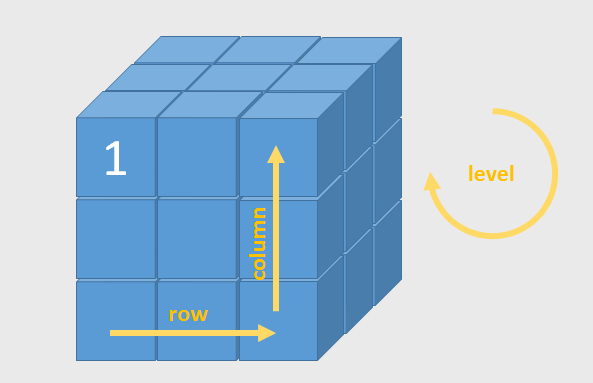
In the next step, the cube is twisted. Assuming that we always keep the “1” square at the upper left position, 18 rotations are possible in one step (rotating the right column by 90/180/270 degrees, rotating the middle column by 90/180/270 degrees, rotating the lower row by 90/180/270 degrees, rotating the middle row by 90/180/270 degrees, rotating the back level by 90/180/270 degrees, and rotating the middle level by 90/180/270 degrees).
The rotations carried out are the key. For my example I took the key MC90, LR270, RC180, ML90, BL270 (for a real application I would have taken a longer key).
Now the letters and numbers are read from the cube (front face with the 1 in the upper left corner, right face, back face, left face, top face, bottom face). The result of my encryption procedure is the following ciphertext:
134CTnILp iwrODWPoV BENbtual5 SjfAmcv6H kJKUdgxGX QRqM2nheF
This looks quite random, considering that the cleartext was “ABCDEF…” and I used only five rotations.
Decryption is straightforward. Take the ciphertext and write it on the cube (front face, right face, …). Then carry out the reverse rotations in the reverse order. Then read the letters from the “1” face, the “2” face and so on.
A challenge
I published a blog post about Mitchell’s cube encryption algorithm two years ago. There were many comments, some of which doubted the security of this method. As far as I know, nobody has ever published a research paper that discusses attacks on this kind of encryption. So, it is still quite unclear whether this algorithm is as secure as it seems and if it can be improved.
To stimulate research in Mitchell’s cube encryption algorithm, I have created a challenge. I took a sentence consisting of 48 letters and encrypted it with a Rubik’s Cube in the way I described it above. Here is the ciphertext I received:
1GDWOHOER GTNTTROI3 AET2NEV5N EIOYR6IBO WEHM4UCOD TNEIEMYET
Can a reader break this cryptogram? If so, which codebreaking method did you use? Is Hill Climbing an option? I’m looking forward to your comments.
Follow @KlausSchmeh
Further reading: The world record crypto challenge






Kommentare (20)