StartseiteCipherbrain

A challenge based on a 1919 cipher tool

Von / 9. November 2019 / 20 Kommentare
Mehr

After the First World War, Italian engineer Luigi Nicoletti invented a transposition cipher tool. Can you break a ciphertext I created with this device?

Most cipher machines and tools implement a substitution cipher. This means that they replace letters with others. The Enigma, the Sigaba, the Kryha and virtually all cipher disks/slides/cylinders are of this kind – just to name a few.

 

Nicoletti’s cipher tool

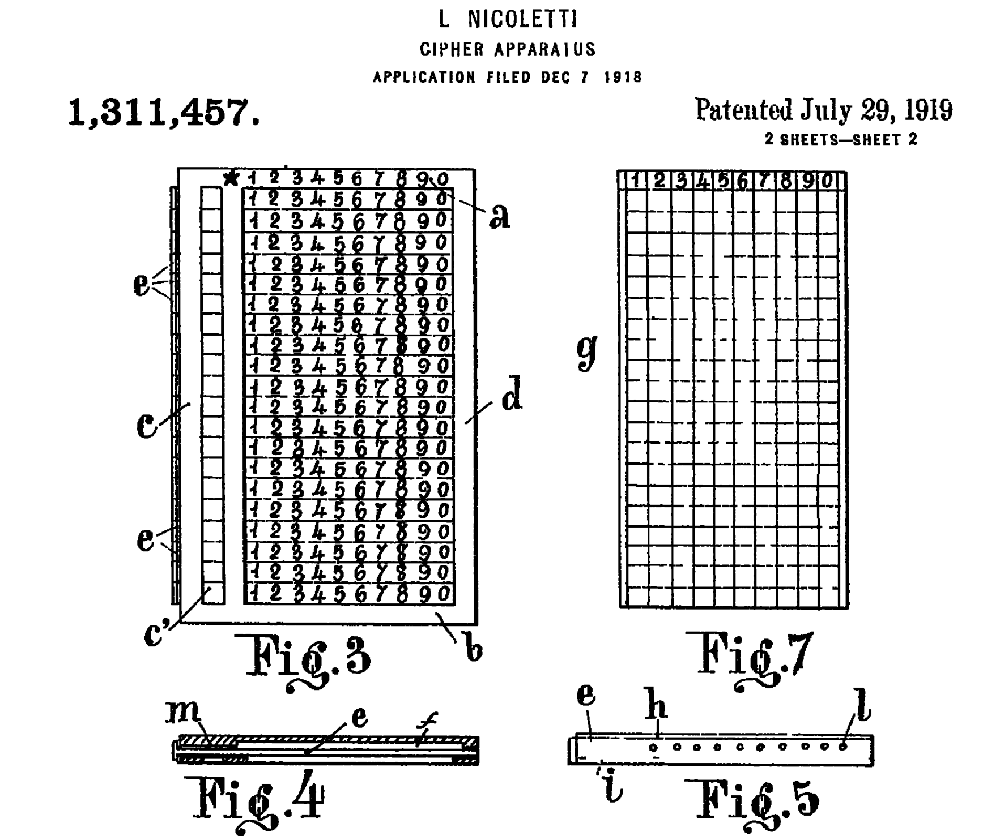
Among the very few devices that realize a transposition cipher (i.e., letters are not replaced, but their order is changed) is a cipher tool invitend by an Italian engineer named Luigi Nicoletti in 1919. The only description of it I know is the patent Nicoletti was granted.

To explain this system, we take the following plaintext:

MEET YOU AT TWENTYNINE MILLNER STREET WEDNESDAY AT MIDNIGHT MYERS

And we take a twenty-digit number as key:

46074 28638 93271 22909

For our plaintext we only use the first ten digits of the key (46074 28638), while the rest is not needed (for a longer text, we would need more). The following picture shows how the device is configured based on the key and how the plaintext is written into it:

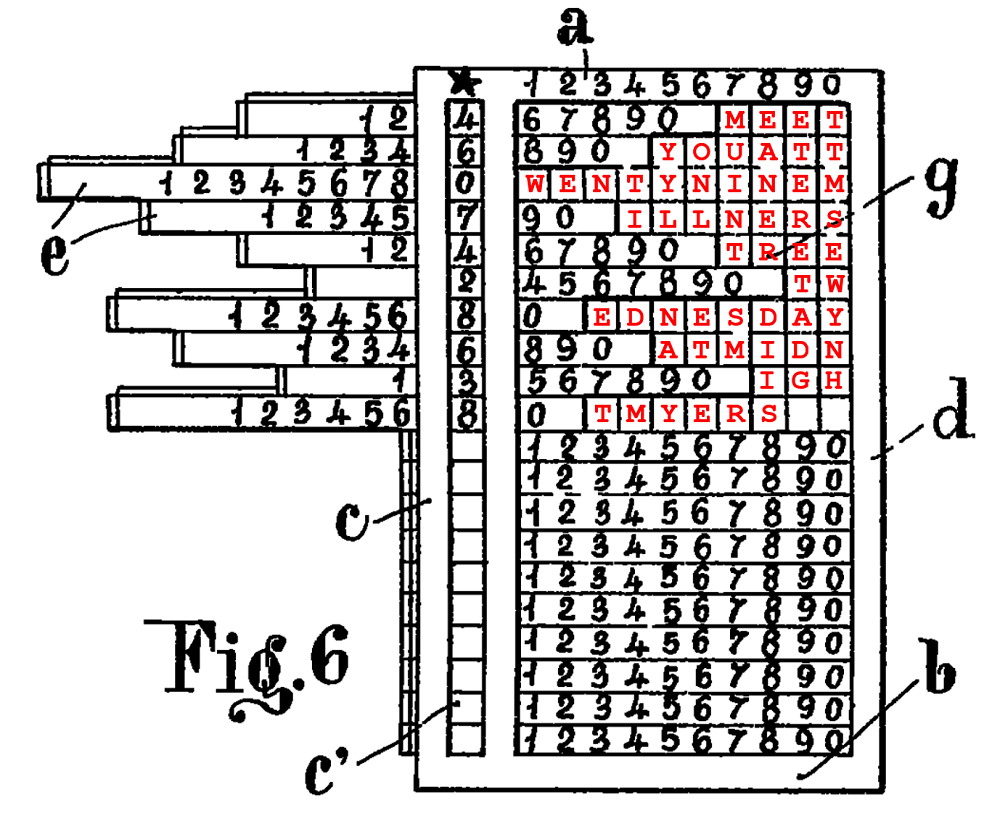
From this picture it should become clear why we only need the first ten digits of the key (and only the first ten lines of the device). A longer message requires more lines and therefore more key digits.

In the second encryption step, the text is read out column-wise. The result is the ciphertext:

WENETTIDMY YLNAYONLET EMUINTSMRE ANERDIISET ERETADGTTM SEWYNH

 

A challenge

The following ciphertext is encrypted in the same way, but with a different key:

TOGURRDTEN OIEOHFETNC MRNNCIMOSI TEIIDBASER SLHESVTOTI
SJMWDEDSEA AIDSSAIAAN TORKWTSAAA MTHIWPOUAE OTLN

Can you break this cryptogram?


Further reading: Can you solve this Cold War encryption challenge?

Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/

Subscribe to Blog via Email

Enter your email address to subscribe to this blog and receive notifications of new posts by email.

Stichworte:
Mehr

Kommentare (20)

  1. #1 anderer Michael
    10. November 2019

    In der 4 und 9 Gruppe sind jeweils 11 Buchstaben, ansonsten immer nur 10 , weil nur 10 Stellen bis auf den Rest. Ist das ein Irrtum oder verstehe ich etwas falsch?. Bzw besteht die Nachricht aus 92 oder 94 Buchstaben?

  2. #2 Klaus Schmeh
    10. November 2019

    @anderer Michael: Thanks for letting me know. Every group should have 10 letters. I changed it. The ciphertext as such stays the same.

  3. #3 Klaus Schmeh
    10. November 2019

    Kuntal Das via Linked-in:
    A nice technique. Thank you for sharing!

  4. #4 TWO
    Geilenkirchen
    10. November 2019

    Is this solved already?

    I am hopelessly stuck on this puzzle.

    Klaus challenged seem yo getting harder and harder.

    I saw the light on his Des challenge, failed the Cold War puzzle and now this.

    What happened to easy beginners puzzles?

  5. #5 Klaus Schmeh
    10. November 2019

    @TWO:
    It’s not solved yet.

    >I saw the light on his Des challenge, failed
    >the Cold War puzzle and now this.
    Perhaps, you can try your luck on encrypted postcards 😉

  6. #6 Dampier
    11. November 2019

    How long would it take with brute force anagram solving (+ dictionary check)?

  7. #7 Narga
    11. November 2019

    I guess to decode (if you are the recipient and have the key) you would configure the bars to the key and then fill in the encrypted text columnwise?

    I think this means that the last digit of the code must actually match the number of letters in that line (or that number+1). In the illustrated example the recipient would have filled the top right T actually in the bottom row behind TMYERS and thus the rightmost column would shift one row up.

  8. #8 Dampier
    11. November 2019

    @Narga, interesting. If the text was shorter – e. g. without MYERS – then there would be only one letter in the last line, and 7 blanks …

  9. #9 Dampier
    11. November 2019

    Of course you can determine the number of blanks at the end, if you know the number of letters …

  10. #10 Narga
    11. November 2019

    What I wanted to say is: I think this cipher does not decrypt correctly (using the right key) if the number of blanks at the end is greater than 1.

  11. #11 Dampier
    11. November 2019

    @Narga, I think, after putting the bars in the correct position, you just need to count the empty boxes linewise, before filling the text in. You count up to the number of letters in your ciphertext. Then the rest is blanks.
    (You could mark every box with a point or stretch out the blanks, then you see where the text belongs.)

  12. #12 Norbert
    11. November 2019

    Here’s my concept for a solver. Haven’t got the time to implement it atm. Maybe someone does?

    1.) Make a presumption about how many rows are involved, and whether the last row is complete or not. If the following steps do not succeed, modify the presumption. For example, let’s assume that all 20 rows are used, and that the last row ends with some blanks.

    2.) Now we can already fill in the rightmost column: It is obviously “TSAAAMTHIWPOUAEOTLN ” (note the blank at the end).

    3.) As a next step, we try to fill in the column second from right. This is, of course, ambiguous, but for each row, there are only two possibilities: Either it has only one letter (skip it) or it has two or more letters (use it). For the last row, there is an extra option of being a blank. For a computer, this is not a huge amount of possibilities, all the more since many combinations can be ruled out: if we assign “one letter only” to too many rows, the ciphertext will not fit anymore in the presumed 20 rows.

    4.) For each combination not ruled out, we perform a bigram scoring. The computer stores the, say, 10,000 best combinations.

    5.) For all of the stored combinations, we perform the same task for the columns third to right. Note that, if a row has previously considered to hold only one letter, this cannot be changed anymore, so the row will be skipped in this and all following steps. For the other rows, there is again a binary decision to take: “only two letters” or “three or more letters” (don’t forget the extra option for the last row). Rule out any combination which will make the ciphertext too long or too short to fill the space. Again, the 10,000 combinations with the best overall bigram score will be kept in memory.

    6.) Repeat this step until all colums are filled. Print out the combination with the best score.

  13. #13 Thomas
    11. November 2019

    Working with an array, before filling in columnwise, in the last – len(key)th – row the rightmost 10(cross sum(key) +10) – len(ciphertext) squares must be marked as void.

  14. #14 Matthew Brown
    11. November 2019

    I’ve managed to assemble the following probable text, but it is not exactly correct;

    THIS IS A MESSAGE FOR JAMES SMITH WAIT UNTIL DAWN THEN PROCEED TO MISSOURI RIVER AND TAKE WOODEN BOATS TO LOCATION

    One intresting quirk of this encryption is that the sum of the key digits must be greater than or equal to the cipher text length but less than the ciphertext length+10. This helps reduce the key space.

    I wrote a script to check millions of these viable keys and recorded the best using a tetragram fitness function. While none were correct, sentence fragments appeared in different places in the deciphered texts like this;

    GTESSWAHITILDAWENTHENPTUNCEEDTOMISSOUORIVERARINDTAKEAWOTTORENBOISLOCATDANISAHISSSAMEJAMDFORMIT
    RIVEKERONDTAWOTRINBOATTISLECATDANDOISISAOTHMESSAFORJAMESSMITHGETILWAINTHDAWENPUNCEEDTOMISSOURA
    THISIDAMESSAFORJSMUEESSMATORNTILWIHONTHDAIEAWRICEEDNPMISSTORIVEOURANDTAKEWOTGDENBOATTSLOCATIAN

    By compositing from different solutions and making some educated guesses I was able to compile the ‘almost’ solution above.

  15. #15 Narga
    11. November 2019

    @Dampier and others: Thanks, you’re right!

  16. #16 Norbert
    11. November 2019

    @Matthew Brown: Great job, almost there! I think the right solution is

    THIS IS A MESSAGE FOR JAMES SMITH WAIT UNTIL DAWN THEN PROCEED TO MISSOURI RIVER AND TAKE WOODEN BOAT TO CAT ISLAND

  17. #17 Norbert
    11. November 2019


    7   THISISA
    5     MESSA
    8  GEFORJAM
    6    ESSMIT
    1         H
    3       WAI
    9 TUNTILDAW
    6    NTHENP
    8  ROCEEDTO
    6    MISSOU
    8  RIRIVERA
    6    NDTAKE
    2        WO
    9 ODENBOATT
    7   OCATISL
    2        AN
    3       D

  18. #18 Christof Rieber
    Wien
    11. November 2019

    An attack could be ‘easy’ to write down the ciphertext from bottom to the top on the right side of a paper. Trying this with e.g. 5, 6, 7,….12 rows, the cleartext shows up (sort of a ‘transposition’).

    This method fails, however, on register cards pulled out only two letters or so….the shorter the word sequences in a row, the harder it’d be to crack.

  19. #19 Klaus Schmeh
    11. November 2019

    @Matthew, Norbert:
    Thank you very much! Matthews solution is almost correct. Norbert’s corrected version is exactly the plaintext I encrypted.
    Congratulations!

  20. #20 Thomas
    11. November 2019

    Mattew, Norbert:
    Good job!