Der Rasterschlüssel 44 ist ein einfaches Verschlüsselungsverfahren, das die Deutschen im Zweiten Weltkrieg als Ersatz für die Enigma nutzten. Blog-Leser Allan Carstairs hat mir eine Challenge zu dieser Methode zur Verfügung gestellt.
English version (translated with Deepl)
Immer wieder erhalte ich Zuschriften von Lesern, die etwa folgenden Wortlaut haben: “Ich habe ein Verschlüsselungsverfahren erfunden. Ein damit verschlüsselter Text lautet: AKSH FKJA WFXS MAKJ. Können Ihre Leser das knacken?”
Leider haben meine Leser an solchen Rätseln erfahrungsgemäß kein großes Interesse. Etwas spannender wird es, wenn das verwendete Verschlüsselungsverfahren bekannt ist und meine Leser lediglich den Schlüssel erraten sollen. Wirklich interessant ist die Sache aber meist nur dann, wenn keine selbstentwickelte Methode verwendet wurde, sondern ein historisch bedeutsames Verfahren. Es gibt eine ganze Reihe von hervorragenden Codeknackern, die sich für solche Methoden interessieren und auch gerne entsprechende Challenges lösen.
Ich habe selbst schon einige derartige Challenges veröffentlicht, was zu erstaunlichen Erfolgen und wissenschaftlichen Veröffentlichungen geführt hat. Hier eine Auswahl:
- Vor über zehn Jahren verschlüsselte ich einen Text mit dem Doppelwürfel-Verfahren. George Lasry konnte es lösen, worüber die Medien ausführlich berichteten.
- Meine Playfair-Challenges haben zu mehreren Rekorden geführt.
- Auch meine Bigramm-Challenges führten zu Rekorden.
Allan Carstairs
Vor ein paar Wochen tauschte ich mich mit Blog-Leser Allan Carstairs, Betreiber einer sehr interesanten Krypto-Challenge-Webseite, zu diesem Thema aus. Dabei kam zur Sprache, dass das Verfahren Rasterschlüssel 44 aus dem Zweiten Weltkrieg äußerst interessant ist. Eine Challenge zu dieser Chiffre war uns nicht bekannt. Allan erstellte daraufhin eine solche.
Doch wer ist Allan Carstairs überhaupt? Er hat mir folgendes über sich geschrieben:
Allan Carstairs is a pseudonym I have adopted for the encrypted puzzle project. I am originally from Zimbabwe, Africa but have lived in other countries for the past twenty years. I originally became interested in codes and ciphers when I was about 9 years of age, in the mid 1970’s, when I bought myself a book on the subject, I think it may have been “Codes and Ciphers, Secret Writing Through The Ages” by John Laffin but I am not sure and I no longer have the book. This sparked my interest in modifying the ciphers detailed in the book to make them more secure.
Back in the 70’s and 80’s my peers were not interested in such things, so I lost interest after a few years. My interest was briefly rekindled when I read “The Code Book” by Simon Singh a few years ago. Then, in September last year I found a reference to the Vigenère cipher on the internet and realised the online interest. I decided I would try my hand again at improving the classical ciphers and as there seems to be more interest now I started the encrypted puzzle website. I am more interested in making classical ciphers secure using methods available to their original designers than breaking ciphers or in the modern digital encryption, about which I know nothing.
Der Rasterschlüssel 44
Der Rasterschlüssel 44 ist ein Verschlüsselungsverfahren, das das deutsche Militär 1944 einführte. Man benötigte für diese Methode nur ein Formular. Ein Chiffrierwerkzeug oder gar eine Maschine war nicht notwendig.
Der Rasterschlüssel war, wie der Doppelkasten, als Ersatz für die Enigma gedacht. Wenn eine solche zu teuer, zu schwer oder kaputt war, was häufig vorkam, war der Rasterschlüssel ab 1944 die vorgesehene Alternative. Das Verfahren wird beispielsweise in meinem Buch “Codeknacker gegen Codemacher” beschrieben. Weitere Beschreibungen finden sich hier, hier und hier.
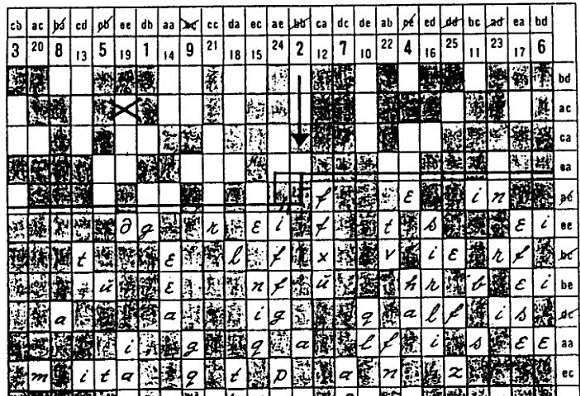
Der Rasterschlüssel 44 ersetzt keine Buchstaben, sondern ändert lediglich deren Reihenfolge. Das Verfahren zählt damit zu den Transpositionschiffren. Das besagte Formular enthält eine Matrix aus 24 Zeilen und 25 Spalten,
in der pro Zeile 15 Felder geschwärzt sind.
Über jeder Spalte steht ein Buchstabenpaar (Bigramm), in dem Buchstaben zwischen a und e vorkommen. Wie man leicht nachrechnet, gibt es genau 25 derartige Bigramme, wodurch pro Spalte eines zur Verfügung steht. Jeder Zeile ist ebenfalls ein derartiges Bigramm zugeordnet, das am Zeilenende steht.
Jedes Feld lässt sich mit Hilfe eines Bigramm-Paars identifizieren. So steht cdaa im Beispiel für das vierte Feld in der vierten Zeile. Die Verteilung der Bigramme über die Spalten und Zeilen ist jeweils zufällig und Teil des Schlüssels.
Über den 25 Spalten der Matrix sind zusätzlich die Zahlen zwischen 1 und 25 notiert. Auch deren Reihenfolge ist zufällig und ein Teil des Schlüssels. Der Schlüssel des Verfahrens besteht damit aus vier Informationen: der Lage der geschwärzten Felder, der Verteilung der Spalten-Bigramme, der Verteilung der Zeilen-Bigramme sowie der Verteilung der Zahlen von 1 bis 25 in den Spalten.
Der Verschlüssler trägt seine Nachricht zeilenweise in die freien Felder des Formulars ein und liest sie anschließend spaltenweise wieder aus. Das Startfeld für das Eintragen der Nachricht kann der Absender selber wählen. Im Beispiel lautet die Nachricht DIES IST EINE KURZE TESTNACHRICHT, und das Startfeld ist cdaa. Da
es sich dabei um ein geschwärztes Feld handelt (es ist zulässig, ein solches zu wählen), beginnt der Text erst im nächsten freien Feld rechts davon, also in bcaa.
Das Auslesen der Nachricht beginnt in einer Spalte, die der Verschlüssler auf eine weiter unten beschriebene Methode berechnet. Handelt es sich dabei beispielsweise um die Spalte mit der Zahl 7, dann notiert der Absender deren Inhalt als ersten Teil des verschlüsselten Texts (im Beispiel ist dies TI). Als zweites
kommt die Spalte mit der Zahl 8 auf gleiche Weise an die Reihe (Z), dann folgte die Spalte mit der Zahl 9 (leer) und so weiter. Nach 25 geht es bei 1 weiter.
Im Beispiel ergibt sich so die verschlüsselte Nachricht TIZIA EHUTT RSHID NISSN EREKC EECT.
Der Nachricht werden die Uhrzeit, die Zahl der Buchstaben und die Bigramme, die das Startfeld markieren, vorangestellt. Letzteres geschieht allerdings nicht im Klartext, sondern mit einer Ersetzungstabelle, die dem Codeknacker nicht bekannt ist.
Die Spalte, die zuerst ausgelesen wird, ermittelt der Absender mit Hilfe der Uhrzeit sowie der Anzahl der Buchstaben der Nachricht. Wird die Nachricht um 10:21 Uhr verschickt und hat sie (wie im Beispiel) 29 Buchstaben, so muss der Verschlüssler 1+0+2+1+2+9 (also 15) zur Spalte des Startfelds hinzuzählen. Ist das Ergebnis größer als 25, dann wird 25 abgezogen. Im Beispiel ergibt sich 17+15–25=7. Das Auslesen beginnt also in Spalte 7.
Die Anweisungen an die Verschlüssler im Zweiten Weltkrieg sahen vor, dass bei einer kürzeren Nachricht sinnlose Begriffe (Wahlwörter) einfgefügt wurden. Das erste und das letzte Wahlwort eines Wahlwort-Blocks wurden durch Verdoppelung der esten bzw. letzten beiden Begriffe angezeigt (z. B. “HHAAUS … KATZZEE”).
Der Empfänger kann die Verschlüsselung wieder rückgängig machen, wenn er das gleiche Formular wie der Absender und die Ersetzungstabelle besitzt.
Die Challenge
Allan Carstairs hat folgende Challenge erstellt, die mit dem Rasterschlüssel 44 entstanden ist:
1244 ---- 198 ---- LGRJ KNGSR EWYTS TGURM AIWSW EDEHP AEIOH ETIRF RCDTA CSSID OEROK ASPEI LARNT FABWT EPLAD LNLOU EENOC TAIGY EAIRI ATRHU TSOAO ESNAR GEHST UIWSF WTSDT PUGKI SADHR EOSRR SDSEY HODEM RAOFW NBITI GTPEM NISBI PSERL CRVRL LCUHT TTESS FOOSH CREHS ELY
Der Klartext ist auf Englisch verfasst. Möglicherweise sind Wahlwörter darin enthalten. Kann jemand diese Challenge lösen?
Follow @KlausSchmeh
Further reading: The Reihenschieber – A cold war encryption device
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/





Kommentare (6)