In 1999 cryptographer Ron Rivest published an encrypted text that was designed to take 35 years to break. Apparently, it has now been solved.
Two years ago, I blogged about the so-called LCS35 cryptogram, a cryptographic challenge created by cryptographer Ron Rivest in 1998. It is listed at position 48 on my Top 50 unsolved encrypted messages list. This challenge depends on the following equation:
To solve the challenge, one needs to calculate the value of w, which is the key that can be used to decrypt the actual cryptogram. The values of t and n are the following:
t = 79685186856218
n = 631446608307288889379935712613129233236329881833084137558899
077270195712892488554730844605575320651361834662884894808866
350036848039658817136198766052189726781016228055747539383830
826175971321892666861177695452639157012069093997368008972127
446466642331918780683055206795125307008202024124623398241073
775370512734449416950118097524189066796385875485631980550727
370990439711973361466670154390536015254337398252457931357531
765364633198906465140213398526580034199190398219284471021246
488745938885358207031808428902320971090703239693491996277899
532332018406452247646396635593736700936921275809208629319872
7008292431243681
The LCS35 challenge was developed by Ron Rivest, known as the “R” in RSA. I took the following picture of him at the RSA Conference 2015 in San Francisco:
Ron Rivest published this challenge on the occasion of the 35th birthday of MIT’s Laboratory for Computer Science (LCS) in 1998. The main design goal was that it would take approximately 35 years to solve it. It is therefore referred to as “LCS35 challenge” or “LCS35 cryptogram”. I wrote my first blog article about it in 2014 (in German).
The LCS35 challenge uses ideas described in the paper Time-lock puzzles and timed-release Crypto by Rivest, Adi Shamir (the “S” in RSA), and David Wagner. To the extent known, the value of w can only be calculated sequentially, which means that it is not possible to parallelize the calculation process. The puzzle can be solved by performing t successive squarings modulo n. There is no known way to perform this computation more quickly, unless one knows the factorization of n, which is the product of two large prime numbers.
Rivest chose the value of t taking into consideration the growth in computational power due to Moore’s Law. He estimated that the puzzle would require 35 years of continuous computation to solve, with the computer used being replaced every year by the fastest model available.
The ciphertext
Once one has found out the value of w, one has to exclusive-or it with the following ciphertext:
427338526681239414707099486152541907807623930474842759553127
699575212802021361367225451651600353733949495680760238284875
258690199022379638588291839885522498545851997481849074579523
880422628363751913235562086585480775061024927773968205036369
669785002263076319003533000450157772067087172252728016627835
400463807389033342175518988780339070669313124967596962087173
533318107116757443584187074039849389081123568362582652760250
029401090870231288509578454981440888629750522601069337564316
940360631375375394366442662022050529545706707758321979377282
989361374561414204719371297211725179287931039547753581030226
7611143659071382
The result is the plaintext, which provides information about the factorisation of n. This allows the solution to be easily verified.
There’s one important problem Rivest mentions in his LCS35 description: If there’s an error in the computation, all the following work will be useless.
Crypto experts will note that there is a relationship between the LCS35 challenge and the RSA algorithm (co-invented by Rivest, Shamir and Leonard Adleman). Both can be broken by factorizing a large prime number product. In this case, the product has 2048 bits. The longest prime number product ever publicly factorized is 768 bits long. It is therefore as good as impossible to attack a 2048 prime number product, which means that the RSA algorithm with a 2048 public key is secure and that the LCS35 challenge can only be solved via the squaring method described above.
The solution
In my 2017 article I wrote: “I am not aware of anyone, who is currently working on the LCS35 challenge. According to Rivest’s LCS35 description, the solution will be publicly announced in 2033. My expectation is that nobody will come up with the solution before.”
Apparently, I was wrong.
Blog readers Jon Paul and George Lasry have informed me that a Belgian computer programmer named Bernard Fabrot has now found the solution. Fabrot sent his solution to CSAIL, the successor of MIT’s Laboratory for Computer Science, which has confirmed its correctness.


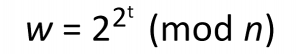


Kommentare (1)