Heute stelle ich ein einfaches aber scheinbar geniales Verschlüsselungsverfahren vor. Erkennt jemand, wie man die scheinbar großartige Erfindung einfach knacken kann?
Königin Alice von Aland will ihrem Kollegen Bob von Beland eine geheime Botschaft zukommen lassen. Sie vertraut jedoch ihrem Boten nicht. Deshalb ersinnt sie folgenden Ablauf:
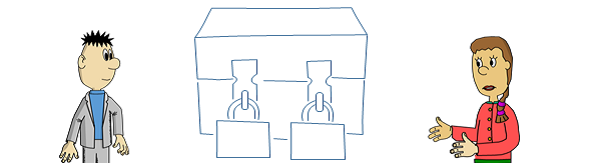
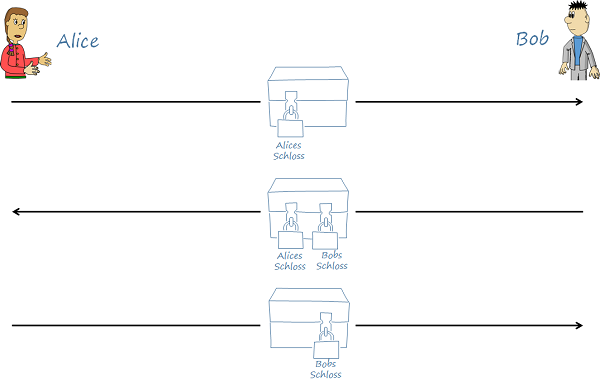
- Alice packt den Zettel mit der Nachricht in eine Kiste, die sie mit einem Vorhängeschloss verschließt. Nur sie hat den passenden Schlüssel. Die Kiste schickt sie an Bob.
- Bob empfängt die Kiste und verschließt sie zusätzlich mit einem zweiten Schloss. Nur er hat den passenden Schlüssel. Dann schickt er die Kiste an Alice zurück.
- Alice empfängt die Kiste, öffnet das erste Schloss mit dem Schlüssel und entfernt es. Anschließend schickt sie die Kiste an Bob zurück.
- Bob empfängt die Kiste, öffnet das zweite Schloss und entnimmt die Botschaft.
Auf dieses Protokoll hat mich freundlicherweise Arnim von Schwedler aufmerksam gemacht. Der Vorteil ist klar: Alice und Bob können eine Botschaft sicher übertragen, ohne sich vorher auf einen identischen Schlüssel einigen zu müssen.
Das Protokoll lässt sich auch in die digitale Welt übertragen (ich nenne es Double-Padlock-Protokoll). Dabei gehen wir davon aus, dass m eine Nachricht ist (z. B. ACHTUNG). a und b seien zufällige Buchstabenfolgen, die so lang wie die Nachricht sind (z. B. KDGENDF und QXDSUFH). a und b werden als One-Time-Pad-Schlüssel verwendet. Dies bedeutet, dass sie buchstabenweise zur Nachricht gezählt werden, wobei A=0, B=1, C=2 usw. gilt (nach 25 wird wieder bei Null angefangen zu zählen).
Nun betrachten wir folgenden Ablauf (er entspricht dem obigen):
- Alice verschlüsselt die Nachricht m mit dem Schlüssel a. Dies notiere ich als m‘=m+a. Alice verschickt m‘ an Bob.
- Bob verschlüsselt m‘ mit dem Schlüssel b. Es gilt also m”=m‘+b. Diese Nachricht m” schickt er an Alice.
- Alice entschlüsselt m” mit dem Schlüssel a. Sie erhält m”’=m”-a. Diese Nachricht m”’ schickt sie an Bob.
- Bob entschlüsselt m”’ mit b. Wie man leicht nachrechnet, erhält er dadurch m.
Dieser Ablauf ist auf den ersten Blick eine revolutionäre Sache. Mit ihm können Alice und Bob eine verschlüsselte Nachricht übertragen, die ein unbefugter Mitleser nicht entschlüsseln kann, ohne sich auf einen Schlüssel einigen zu müssen. Zwar erfordert der Ablauf drei verschickte Nachrichten, doch dieser Zusatzaufwand ist geradezu minimal im Vergleich zu digitalen Zertifikaten, einer Public-Key-Infrastruktur und den sonstigen Dingen, die man in der modernen Kryptologie zur Lösung des Schlüsselaustausch-Problems verwendet.
Stehen wir in der modernen Kryptologie also vor einer Revolution? Leider nein, denn die Sache hat einen Haken. Findet ihn jemand?
Zur Veranschaulichung hier noch ein Beispiel. Wir nehmen an, dass der (unzuverlässige) Bote folgende drei Nachrichten überträgt: m‘=”THZY”, m”=”EVRB”, m”’=”ESKW”. Was kann der Bote (oder sonst ein Bösewicht, der mit ihm kooperiert) damit anfangen?
Follow @KlausSchmeh



Kommentare (48)