Die Aargauer Kantonsbibliothek hat mich um Unterstützung gebeten. Wer kann diesen verschlüsselten Brief des französischen Marschalls Nicolas de Catinat dechiffrieren?
“Ich bin auf der Suche nach einer Dechiffrierung eines Briefs von Nicolas de Catinat auf Ihren Namen gekommen”, schrieb mir Frau Dr. Ruth Wüst von der Aargauer Kantonsbibliothek in der Schweiz.
Frau Wüst ist gerade dabei, das Archiv der Familie Zurlauben (ca. 32’000 Seiten) aus der frühen Neuzeit online zu stellen. In diesem Archiv ist sie auf einen verschlüsselten Brief gestoßen, der auf den 15. September 1702 datiert ist. Geschrieben wurde er im “Camp d’Ingleshein”. Historiker vermuten, dass die Unterschrift von Nicolas de Catinat, einem hochrangigen französischen Offizier und “Marschall von Frankreich”, stammt. Als Empfänger vermutet man den Lieutenant General Beat Jakob Zurlauben. Der Brief ist auf Französisch verfasst.
Die Zurlaubens waren eine bedeutende Magistratenfamilie aus dem Schweizer Kanton Zug, die über mehr als 200 Jahre einflussreiche politische, militärische und kirchliche Positionen besetzte. Die männlichen Familienmitglieder kämpften als Söldner in den Armeen Frankreichs, Savoyens, Spaniens und des Heiligen Stuhls. Die Familie unterhielt von 1619 bis zur Französischen Revolution fast ohne Unterbrechung eine Kompanie im königlichen Garderegiment in Frankreich.
Drei Seiten mit einem Nomenklator verschlüsselt
Der Brief hat drei Seiten. Hier ist Seite 1:
Hier ist Seite 2:
Auf Seite 3 findet sich nur noch Klartext:
Ein Nomenklator steckt dahinter
Wer Klausis Krypto Kolumne öfters liest, erkennt schnell, um welche Art von Verschlüsselung es sich hier handelt: um einen Nomenklator. Ein Nomenklator sieht für jeden Buchstaben des Alphabets sowie für wichtige Wörter je eine Zahl (oder eine Buchstabengruppe) vor. Ein einfaches Beispiel:
A=1, B=2, C=3, D=4, …, Z=26, HUND=99, KATZE=123, MAUS=180
Der Ausdruck HUND KATZE UND MAUS verschlüsselt sich damit in 99, 123, 21, 14, 4, 180.
Um eine Häufigkeitsanalyse zu erschweren, kann der Verschlüssler bei manchen Nomenklatoren zwischen mehreren Zahlen für denselben Buchstaben wählen. Wenn ein Nomenklator besonders viele Einträge umfasst, spricht man von einem Codebuch. Wo genau der Übergang zwischen einem Nomenklator und einem Codebuch liegt, ist nicht festgelegt, man könnte die Grenze bei etwa 1000 Einträgen ziehen.
Codebücher und Nomenklatoren waren ab dem 14. Jahrhundert bis nach dem Zweiten Weltkrieg in Gebrauch. Vor Aufkommen des Computers bildeten sie vermutlich die meistverwendete Form des Verschlüsselns überhaupt. Frühe Codebücher und Nomenklatoren lassen sich heute meist lösen (ein Beispiel ist der Mann mit der Eisernen Maske), doch ab etwa 1800 erreichte diese Technik eine Qualität, bei der auch heutige Codeknacker oft passen müssen. Ungelöste Codebuch- bzw. Nomenklator-Nachrichten sind etwa das Seidenkleid-Kryptogramm oder das van-Gelder-Kryptogramm. Auch das Ohio-Kryptogramm dürfte dazu gehören.
Leider gibt es meines Wissens momentan weltweit keinen Spezialisten für das Knacken von Codes und Nomenklatoren. Dabei gäbe es für so jemanden viel zu tun, denn in den Archiven schlummern noch unzählige Kryptogramme dieser Art.
Wer kann das Catinat-Kryptogramm lösen?
Der von Catinat verwendete Nomenklator sieht Zahlen zwischen 1 und 500 vor. Zweistellige Zahlen sind dabei deutlich häufiger als zu erwarten wäre. Dies könnte bedeuten, dass die Buchstaben des Alphabets mit zweistelligen Zahlen kodiert wurden, während für ganze Wörter größere Zahlen verwendet wurden (viele Nomenklatoren waren so aufgebaut, obwohl eine solche Trennung aus Sicherheitsgründen eigentlich vermieden werden sollte). Leider sind keine Wort-Zwischenräume zu erkennen, was die Sache deutlich erschwert.
Kann jemand den verschlüsselten Brief von Nicolas de Catinat lösen? Nicht nur in der Aargauer Kantonsbibliothek würde man sich freuen.
Follow @KlausSchmeh
Zum Weiterlesen: Wer knackt die verschlüsselte Nachricht von Kardinal Soglia?




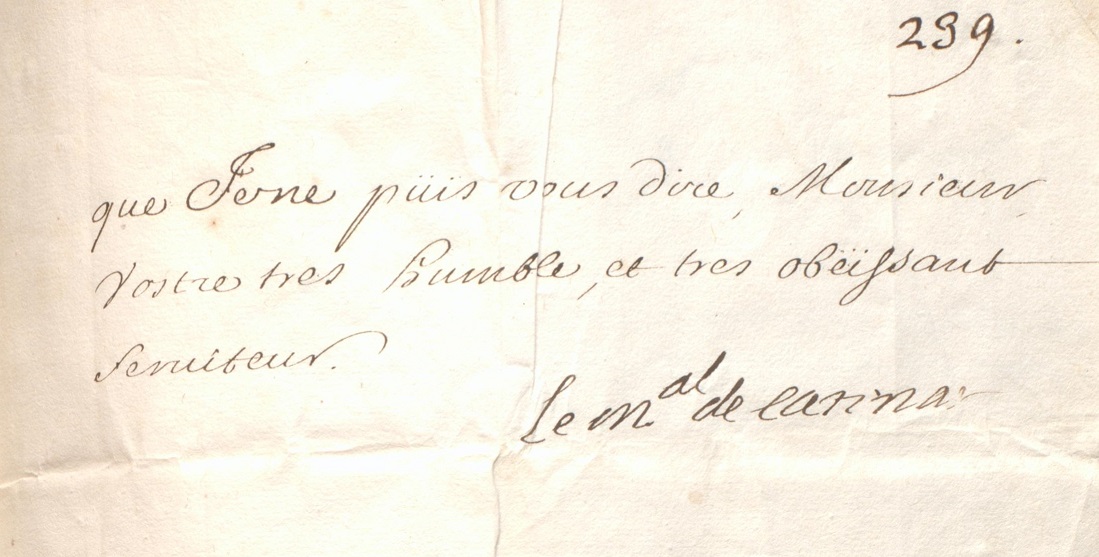

Kommentare (46)