Blog reader Bart Wenmeckers has solved a 19th century cryptogram I recently introduced with Hill Climbing. A few diagrams he provided give me the chance to explain how this powerful technique works.
George Lasry, an Israeli of French decent, is one of the best codebreakers I know. He is especially good, when the cipher algorithm in question is known and the goal is to find the key.
Hill Climbing
George’s favorite method to break encryptions is Hill Climbing. Other codebreakers, including Nils Kopal, Armin Krauß, Jim Gillogly and Dan Girard have been very successful with Hill Climbing, too. For instance, Jim Gillogly solved hundreds of IRA cryptograms from the 1920s with Hill Climbing, as described in his book Decoding the IRA. Dan Girard broke a Playfair cryptogram from the Cheltenham Listening Stones in a similar way. Hill Climbing has become the super algorithm of classic codebreaking in recent years.
Using Hill Climbing for decrypting a ciphertext works as follows (we assume that the cipher algorithm is known and that the goal is to find the key):
- Construct a key at random and use it to decrypt the ciphertext.
- Take the result as input to a function (“fitness function”) that rates the correctness of the result (for instance, based on whether the letter frequencies ressemble the ones of English text).
- Change the key slightly (according to a “mutation rule”) and use it again to decrypt the ciphertext. Rate the result again with the fitness function. If the rating is better now, keep the current key, otherwise reload the previous one.
- Carry on this procedure until the rating doesn’t improve any more.
If we are lucky, the maximum rating we have found indicates that the last key is the correct one.
Codebreaking with Hill Climbing only works if small changes in the key cause small changes in the cleartext. This is the case for many classical encryption algorithms, including the Columnar Transposition, the Double Columnar Transposition, and the Fleissner grille (just to name a few). The Enigma can also be attacked with Hill Climbing.
In contrast, Hill Climbing doesn’t work in modern cryptanalysis, as modern encryption algorithms, like AES, DES, and PRESENT, are designed to be so-called random oracles. This means that if only one bit is changed in the cleartext or the key the ciphertext changes completely. This is also referred to as “avalanche effect”. If an encryption algorithm implements the avalanche effect properly, Hill Climbing is completely worthless.
How Bart Wenmeckers solved the Baring cryptogram
On March 16 I introduced a cryptogram from the 19th century created by British priest and novelist Sabine Baring-Gould (1834–1924) .
Blog reader Thomas solved this cryptogram within a few hours. He assumed that the cipher method used was a simple letter substitution, which can be broken with frequency analysis (i.e. taking into account that the E is the most frequent letter in English texts) and guessing words (as the first word of this cryptogram consists of only one letter, it is probably A or I). Here’s the solution: A BIRD IN THE HAND IS WORTH TWO IN THE BUSH.
Bart Wenmeckers from New Zealand solved the Baring cryptogram, too. He used Hill Climbing. At first view, this technique looks a little oversized for such a simple encryption method. However, while letter counting and word guessing are well-suited for manual codebreaking, writing a Hill Climbing computer program is probably easier than writing one that applies frequency analysis and guesses words. In addition, Bart’s program gives us the chance to see how Hill Climbing works in practice.
At first, Bart created a transcription of the cryptogram:
The new ciphertext is: A BCDE CF GHI HAFE CJ KLDGH GKL CF GHI BNJH.
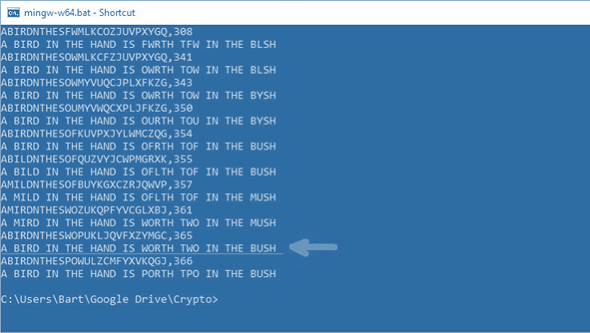
The following screenshot shows the last ten steps Barts Hill Climbing solver took in order to improve the rating delivered by the fitness function.
As you can see, the first key shown in the screenshot is the following:
ABCDEFGHIJKLMNOPQRSTUVWXYZ ABIRDNTHESFWMLKCOZJUVPXYGQ
This key resulted in the following cleartext: A BIRD IN THE HAND IS FWRTH TFW IN THE BLSH. This cleartext was rated 308 by the fitness function. After a few tries (the screenshot doesn’t tell how many) the solver found a better cleartext (rated 341) and thus a better key. With each improvement of the rating the cleartext gets closer to the correct one.
My personal favorite cleartext is A MIRD IN THE HAND IS WORTH TWO IN THE MUSH (361 points). However Bart’s solver found a better one (365 points): A BIRD IN THE HAND IS WORTH TWO IN THE BUSH. Interestingly, the solver didn’t realize that this guess was the correct one. Instead, it found a seemingly even better cleartext (366 points): A BIRD IN THE HAND IS PORTH TPO IN THE BUSH.
Here are the data of another run of Bart’s solver:
AYISJNTHEDFCBWLVOPUQKXMGRZ,263 A YISJ IN THE HANJ ID FCSTH TFC IN THE YWDH AYISJNTHEDFCBPLVMWUQOKXGRZ,264 A YISJ IN THE HANJ ID FCSTH TFC IN THE YPDH AYISJNTHEDFRBPLVMWUQOKXGCZ,287 A YISJ IN THE HANJ ID FRSTH TFR IN THE YPDH AYISMNTHEPFRBDJXLWCQOKZGVU,306 A YISM IN THE HANM IP FRSTH TFR IN THE YDPH AYISLNTHEPFRBDJXMWCQOKZGVU,313 A YISL IN THE HANL IP FRSTH TFR IN THE YDPH AYISLNTHEFBRPDGMOJZWUVQXKC,314 A YISL IN THE HANL IF BRSTH TBR IN THE YDFH AYISLNTHEMBRPDUGCFQJZVXKOW,321 A YISL IN THE HANL IM BRSTH TBR IN THE YDMH AYISLNTHEMBUQDVWCGPJZRXKOF,323 A YISL IN THE HANL IM BUSTH TBU IN THE YDMH ARISDNTHEMBOUFQWKXCZGPVLYJ,327 A RISD IN THE HAND IM BOSTH TBO IN THE RFMH ARISDNTHEMOBUFQWKXCZGPVLYJ,331 A RISD IN THE HAND IM OBSTH TOB IN THE RFMH ARISDNTHEMOPUFQWKXCZGBVLYJ,333 A RISD IN THE HAND IM OPSTH TOP IN THE RFMH ARISDNTHEGOPZFQWUXVJMBCLYK,334 A RISD IN THE HAND IG OPSTH TOP IN THE RFGH ARISDNTHEGOFZPQWUXVJMBCLYK,343 A RISD IN THE HAND IG OFSTH TOF IN THE RPGH ARISDNTHEMOFZPQWUXVJGBCLYK,347 A RISD IN THE HAND IM OFSTH TOF IN THE RPMH ARISDNTHEMOFCYBKWXZJVLUGQP,348 A RISD IN THE HAND IM OFSTH TOF IN THE RYMH ARISDNTHELOFZUJMBXCKGVQPYW,349 A RISD IN THE HAND IL OFSTH TOF IN THE RULH ARILDNTHESOFJMXVUWGQCPBKZY,354 A RILD IN THE HAND IS OFLTH TOF IN THE RMSH ARILDNTHESOFVUKMXGPYZJWCBQ,355 A RILD IN THE HAND IS OFLTH TOF IN THE RUSH AMILDNTHESOFVUJQXGPYZKWCBR,357 A MILD IN THE HAND IS OFLTH TOF IN THE MUSH AMIRDNTHESCOYUBQVXLPWZGJFK,358 A MIRD IN THE HAND IS CORTH TCO IN THE MUSH ABIRDNTHESWOYUMXVQCZJLKGPF,365 A BIRD IN THE HAND IS WORTH TWO IN THE BUSH ABIRDNTHESPOGUJMQXZYKCWLFV,366 A BIRD IN THE HAND IS PORTH TPO IN THE BUSH
Again, the solver found the correct cleartext but didn’t realize it. The fitness function Bart used is based on the frequency of four-letter groups (quadgrams) in the English language. The key mutation is a random source destination swap of the key table.
I think Bart’s solver is a great tool for solving substitution ciphers automatically. In addition, it does a great job in visualizing how Hill Climbing works. Thank you very much to Bart for this great input.
Follow @KlausSchmeh
Further reading:
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/


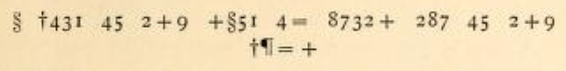



Kommentare (3)