Italian cryptologist Luigi Sacco left behind a text encrypted with a Fleissner grille. Paolo Bonavoglia and Bart Wenmeckers, both readers of this blog, solved it.
Next week the Euro HCC, a conference about the history of cryptology, will take place in Bratislava, Slovakia. I will take part in this event and I am looking forward to seeing many interesting people from the crypto history scene, some of which I have never met before.
For instance, Paolo Bonavoglia from Italy will be an attendant of the Euro HCC. Frequent readers of Klausis Krypto Kolumne might remember that Paolo solved an encrypted book written by 19th century poet and patriot Pietro Giannone (1791–1872). Paolo will give a presentation about this codebreaking success in Bratislava.
Sacco’s Fleissner cryptogram
A few days ago Paolo Bonavoglia published an encrypted text the Facebook group Cryptograms & Classical Ciphers. This text stems from his grandfather Luigi Sacco, who was a notable cryptologist and crypto book author. Here it is:
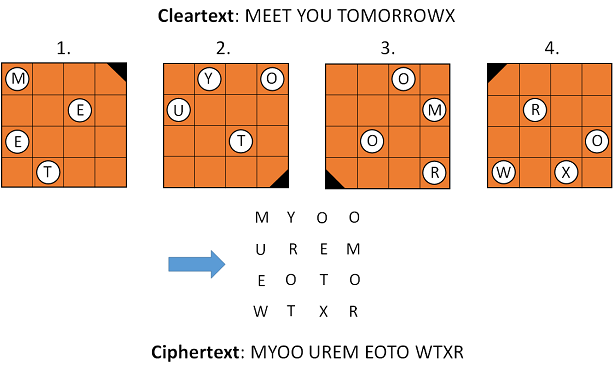
It seems likely that Sacco used a so-called Fleissner grille to create this cryptogramm. A Fleissner grill is a square stencil with holes. The following picture was provided to me by Andreas Önnerfors:
Here’s how a Fleissner grille works (the stencil is used four times, each step is followed by a 90 degree turn):
A Fleissner encryption represents a transposition cipher. This means that no letter substitution takes place. Only the order of the letters is changed.
Bart Wenmecker’s solution approach
A person I won’t meet in Bratislava, although he is a codebreaking expert, is Bart Wenmeckers. Bart lives in New Zealand, which is literally half a world away from the conference site. Too bad, with his cryptologic expertise Bart would certainly be an enrichment for this event.
Paolo already knew the solution of Sacco’s Fleissner cryptogram, but he did not immediately publish it on Facebook. Bart Wenmeckers took the chance to look for a solution himself.
Like many other current specialists for breaking classical ciphers (e.g., George Lasry, Nils Kopal, Armin Krauß, Jim Gillogly and Dan Girard), Bart makes frequent use of Hill Climbing. In recent years, Hill Climbing has become the super algorithm for solving historical ciphers. Among others, the open source software CrypTool 2 features a Hill Climbing function.
Using Hill Climbing for decrypting a ciphertext works as follows (the cipher algorithm must be known, the goal is to find the key):
- Construct a key at random and use it to decrypt the ciphertext.
- Take the result as input to a function (“fitness function”) that rates the correctness of the result (for instance, based on whether the letter frequencies ressemble the ones of English text).
- Change the key slightly (according to a “mutation rule”) and use it again to decrypt the ciphertext. Rate the result again with the fitness function. If the rating is better now, keep the current key, otherwise reload the previous one.
- Repeat this procedure until the rating doesn’t improve any more.
If one is lucky, the key candidate with the maximum rating is the correct one.
Codebreaking with Hill Climbing only works if small changes in the key cause small changes in the cleartext. This is the case for many classical encryption algorithms, including the Columnar Transposition, the Double Columnar Transposition, and the Fleissner grille (just to name a few). The Enigma can also be attacked with Hill Climbing.
However, Hill Climbing doesn’t work for modern ciphers like DES or AES, as they are designed to be “random oracles”, i.e., even a small change in the input (key and cleartext or ciphertext) completely changes the output (ciphertext or cleartext). This (desired) phenomenon is also referred to as “avalanche effect”.
Bart’s Hill Climbing steps
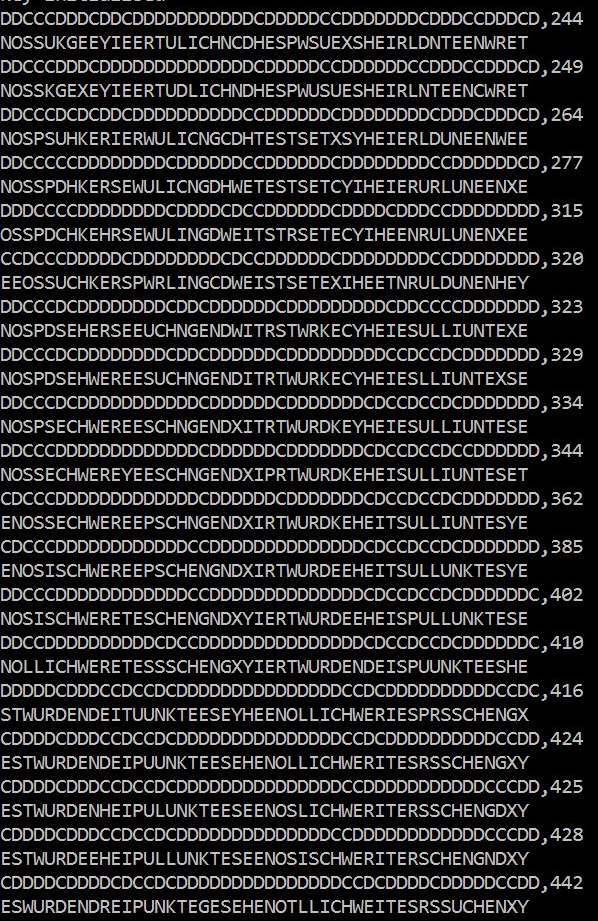
It’s always fascinating to look at the single steps of a successful Hill Climbing attack and to see how the rating of the fitness function grows and how the cleartext candidates more and more mutate to the correct one. Here’s the protocoll of Bart’s Hill Climbing attack on Sacco’s Fleissner cryptogram:
The sequences of C’s and D’s identify the stencil that was used for decrypting. NOSSUK… is the first cleartext candidate. It receives a rating of 244. About 30 steps later the rating has risen to 442, while the cleartext candidate has evolved to: ESWURDENDREI… This is clearly a German text.
The solution is the following: ES WURDEN DREI PUNKTE GESEHEN OTLLICH WEITESRSUCHEN XY.
This cleartext obviously contains a few mistakes. XY, the last two letters, were added as filling material. Here’s a corrected version: “Es wurden drei Punkte gesehen, östlich weitersuchen.” (“Three points were seen, seek further eastwards”.)
An open question
In addition to the Fleissner cryptogram Sacco’s notebook contains a second transposition of the same cleartext:
Does a reader know how exactly Sacco created this cryptogram? Is there a simple rule that leads from the cleartext to this ciphertext? Any help is welcome.
Editted to add (2020-05-02): Tobias Schrödel has pointed out that the solution of the Fleissner cryptogram is mentioned on the same notebook page as the ciphertext (the numbers in the square indicate the resulting transposition):

Follow @KlausSchmeh
Further reading: How my readers solved the Fleissner challenge
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/






Kommentare (11)