Today I am going to introduce a simple asymmetric encryption system. It’s not suitable for practical use, but very helpful for explaining how public key cryptography works.
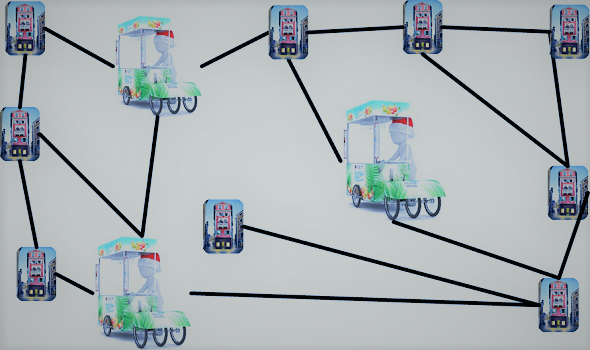
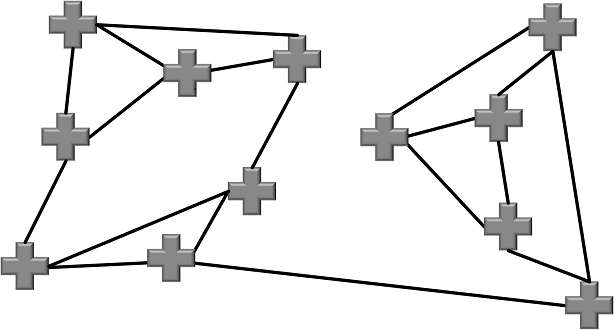
Suppose we have a map showing 12 cross sections, which are connected via a number of streets.
Now the question is: Can you place three ice cream vans on three of the cross sections such that every van serves exactly for cross sections (i.e., the cross section it stands on and three cross sections that are connected to this one). Every cross section that doesn’t have an ice cream van of its own needs to be connected to exactly one cross section that has one.
Ice Cream Van puzzles
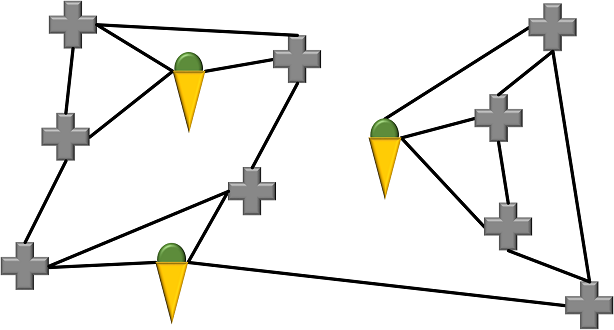
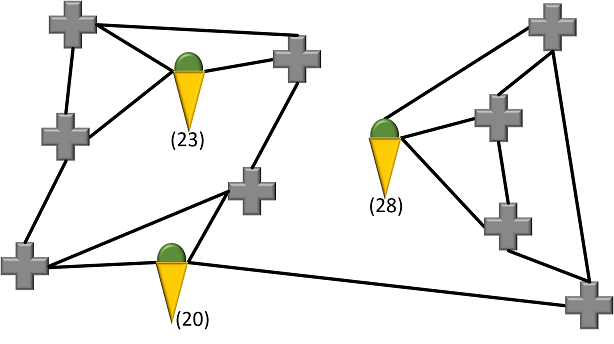
Here’s a solution to this puzzle:
As you see, every ice cream van serves the cross section it stands upon and is connected to exacly three others. If you’re standing on a cross section that doesn’t have an ice cream van, you will find one on a cross section that is directly connected.
The Ice Cream Van problem (also known as the Minimum Dominating Set problem) is quite difficult to solve, especially if we deal with, say, a few hundred cross sections with each ice cream van needing to be connected to, say, exactly ten of them.
Readers with a mathematical background certainly know that the Ice Cream Van problem belongs to graph theory. It is NP-complete.
While an Ice Cream Van puzzle is hard to solve, it is quite easy to create one. Just draw a number of ice cream vans and connect, say, three cross sections with each one. Then connect some of the cross sections with each other such that every ice cream van and every cross section has exactly three connections.
The Ice Cream Van crypto system
Based on the Ice Cream Van problem one can define a public key encryption system (a more detailed description is available here).
In the first step, Alice creates an Ice Cream Van puzzle. She uses the map with the ice cream vans as her private key, while the map version with no vans shown serves as public key. We’ll use the maps shown above.
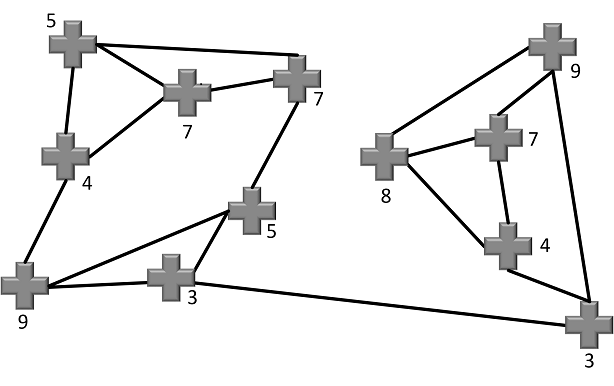
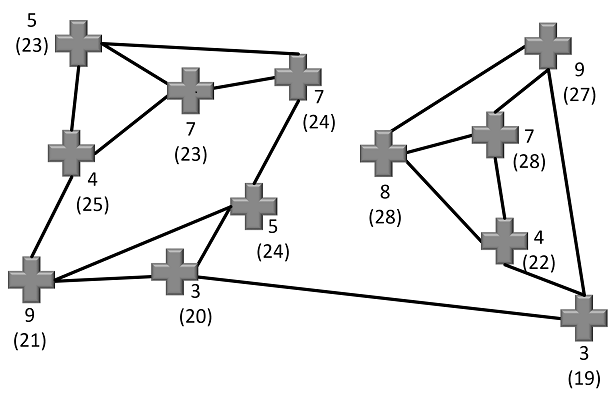
Now suppose that Bob wants to encrypt the message “71” to Alice (this is a very short message consisting of only one number; if we use larger maps, larger numbers can be encrypted). To do so, Bob marks each cross section in Alice’s public key with a number, such that all 12 numbers sum up to 71.
In the next step Bob adds to each number the sum of this number and the numbers of the three neighbors:
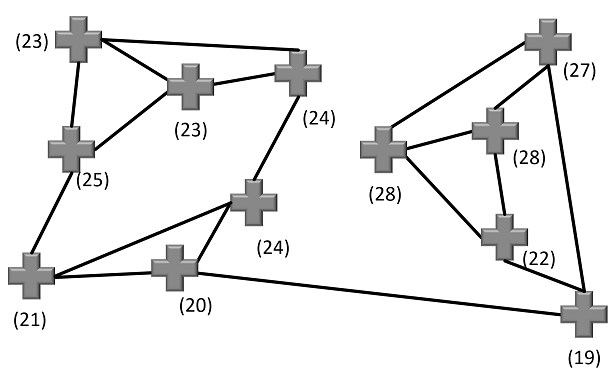
Next, Bob deletes the original numbers and sends the map with the sums to Alice:
For an eavesdropper it is not possible (or at least pretty difficult) to derive the message (“71”) from this infomation. However, for Alice it is easy. All she needs to do is sum up the bracketed numbers asserted to the ice cream vans (note that the position of the vans is only known to Alice):
As you see, these numbers (23, 28 and 20) sum up to 71. Alice has decrypted the message.
In theory, the Ice Cream Van crypto system works quite well. For instance, it can be used to transmit an encrypted key for a symmetric cipher. However, mathematicians have found a way to break this method (this attack is explained in the paper I used as the source for this post). Nevertheless, the Ice Cream Van crypto system is very helpful for explaining how public key encryption works. Even school children can understand this algorithm. So, before you try to explain RSA or Elliptic Curve crypto systems to somebody, it might make sense to give an introduction to the Ice Cream Van algorithm first.
Follow @KlausSchmeh
Further reading: How a spy hid a message in an alleged chess problem
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/


Kommentare (3)