At the 44CON, a London-based hacker conference, I gave a talk about Post-Quantum cryptography. Among other things, I explained the GGH algorithm – using snail terminology.
How to Explain Post-Quantum Cryptography to a Middle School Student, was the title of a presentation I gave at the 44CON conference in London last Friday.
Post-quantum cryptography, one of the hottest topics in IT security today, addresses asymmetric crypto systems that are not prone to quantum computers. Virtually all asymmetric crypto systems currently in use (especially, Diffie-Hellman, RSA, DSA, and Elliptic Curve crypto systems) are not post-quantum. They will be useless, once advanced quantum computers will be available. Quantum computer technology has made considerable progress in recent years, with major organisations, like Google, NSA, and NASA, investing in it.
Post-quantum cryptography uses advanced mathematical concepts. Even if one knows the basics of current asymmetric cryptography (integer factorisation, discrete logarithms, …), Post-quantum algorithms are hard to understand. The goal of my presentation was to explain post-quantum cryptography in a way that is comprehensible for non-mathematicians.
The following video shows a short excerpt from my talk:
One of the post-quantum methods I explained is the so-called GGH algorithm (named for its inventors Goldreich, Goldwasser, and Halevi). GGH is a lattice-based crypto algorithm. But how can one explain lattice-based cryptography in an entertaining and easy-to-understand way? My co-worker Daniel Rocholz from cryptovision had a great idea: explain it from the point-of-view of a snail. The following presentation slides show how I put Daniel’s idea into practice.
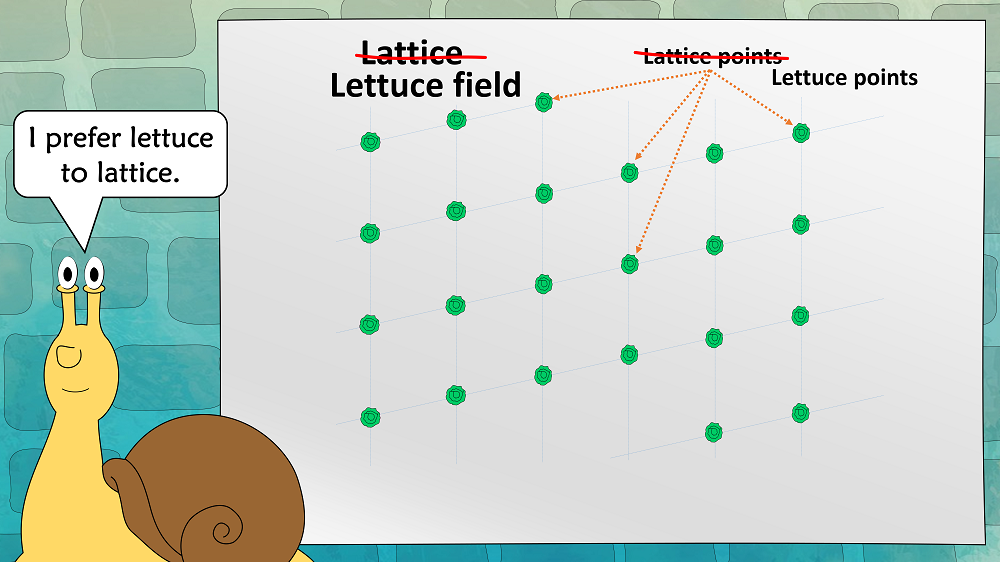
First of all, a snail certainly prefers lettuce to lattice:
This means that in our explanations we replace lattices with lettuce fields:
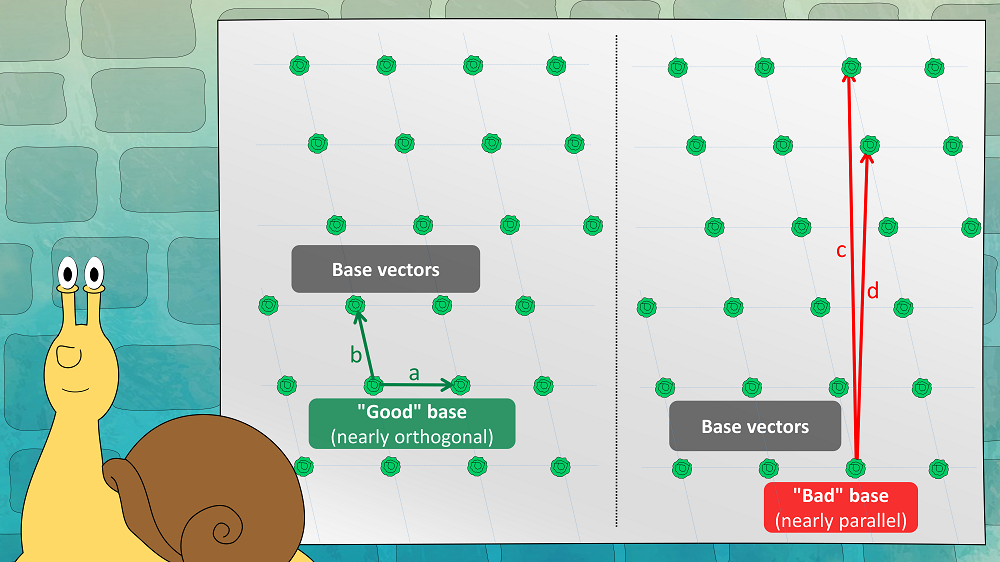
A lettuce field is defined by a set of vectors. This set is referred to as a “base”; the vectors are named “base-vectors”. In the two-dimensional case, there are two base-vectors. As can be seen in the next picture, there are good bases (nearly orthogonal) and bad bases (nearly parallel) for the same lettuce field:
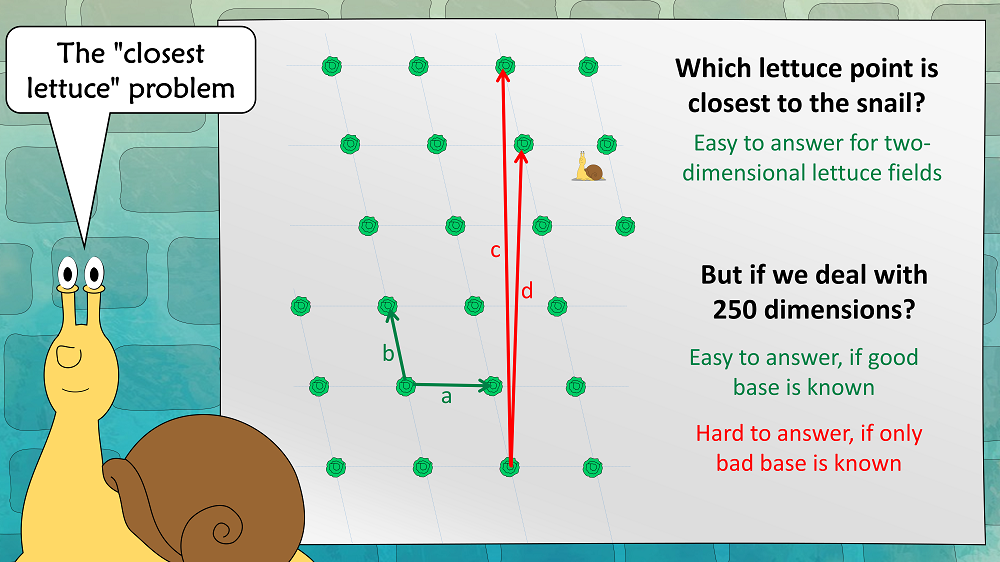
We now assume that a snail is placed somewhere in the lettuce field. As a snail is very slow, it has an interest in finding the closest lettuce. This results in the “closest lettuce” problem:
If we assume that we are in a high-dimensional lettuce field, this problem is easy to solve with a good base, but hard to solve with a bad base.
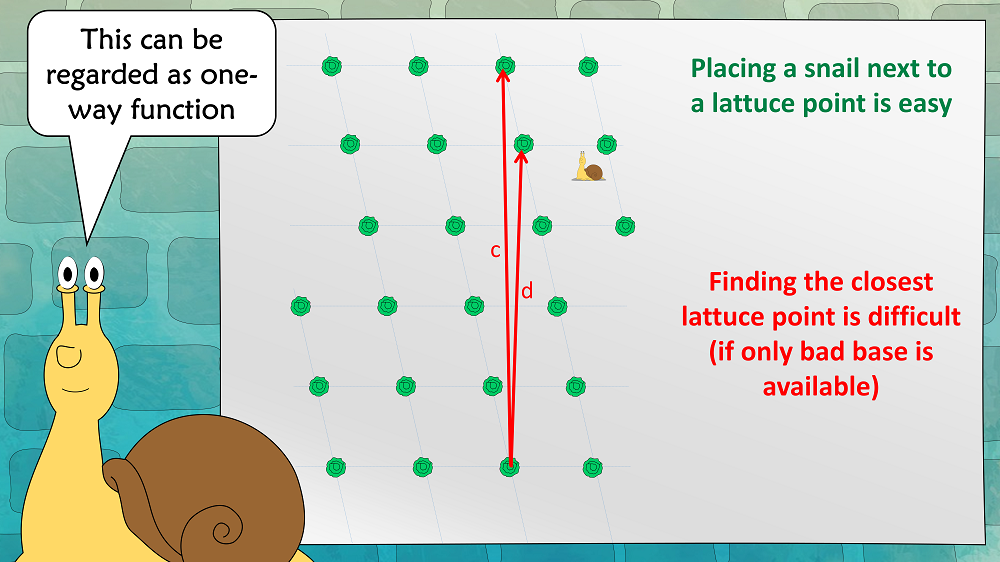
This problem can also be regarded as a one-way function:
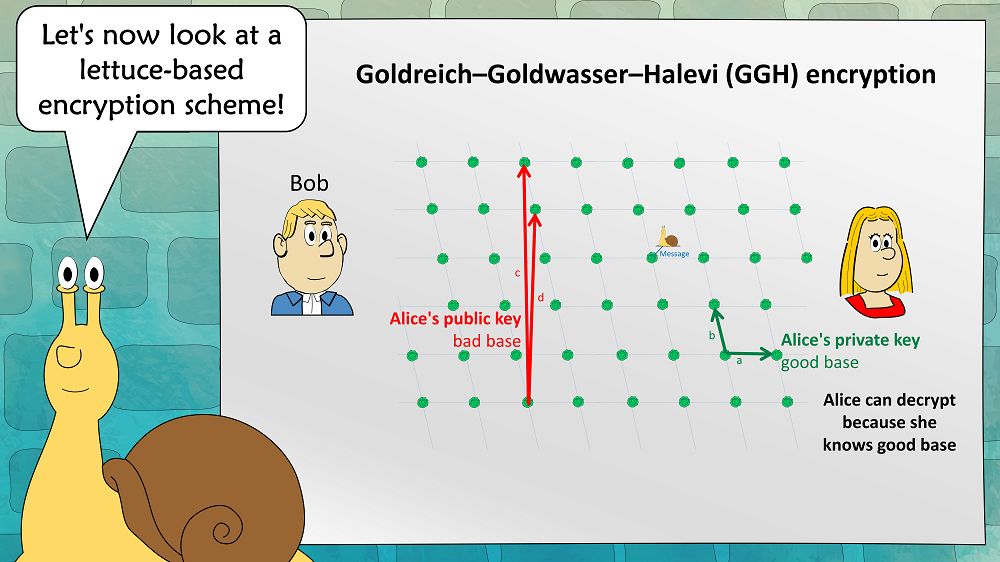
Now we can define the GGH asymmetric encryption scheme:
Alices public key is a bad base, her private key is a good base. To encrypt, Bob places a snail near a lettuce. The vector between the snail and the lettuce is the cleartext (in practice, the lettuce field is about 250-dimensional, which means that this vector can easily encode a 128 bit message). Alice can easily find the closest lettuce (and thus decrypt the message), as she knows a good base. An attacker can’t, as he has only a bad base.
That’s it. This isn’t very difficult, is it?
Unfortunately, GGH has proven insecure, so it should not be used in practice. However, there are other lattice-/lettuce-based encryption schemes, that are considered secure, like NTRU, (R)LWE, and New Hope. 27 algorithms of this kind have been handed in to the NIST Post-Quantum Competition. I’m pretty sure that several of them will be among the winners.
Follow @KlausSchmeh
Further reading:
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/




Kommentare (8)