Crypto history expert Frode Weierud has provided me a number of unsolved German cipher messages from the Second World War. Can a reader break them?
Three weeks ago, I introduced the double box (Doppelkasten) cipher, a manual encrption method used by the Germans in the Second World War. My article included a challenge ciphertext consisting of 100 letters. Several of my readers tried to solve this cryptogram with hill climbing or other means, but to no avail. This surprises me, as the codebreaking programs written by my readers have proven quite powerful when it comes to solving manual ciphers. The double box might be more secure than I thought.
The double box
One thing that has meanwhile become clear to me is that there are several variants of the double box and that it is unclear which one(s) the Germans actually used (thanks to Seth, Richard Bean and others for their comments with respect to this issue). While this doesn’t affect my double box challenge, as the variant I used is the one I specified, it is still interesting to know how the soldiers in World War II employed this method.
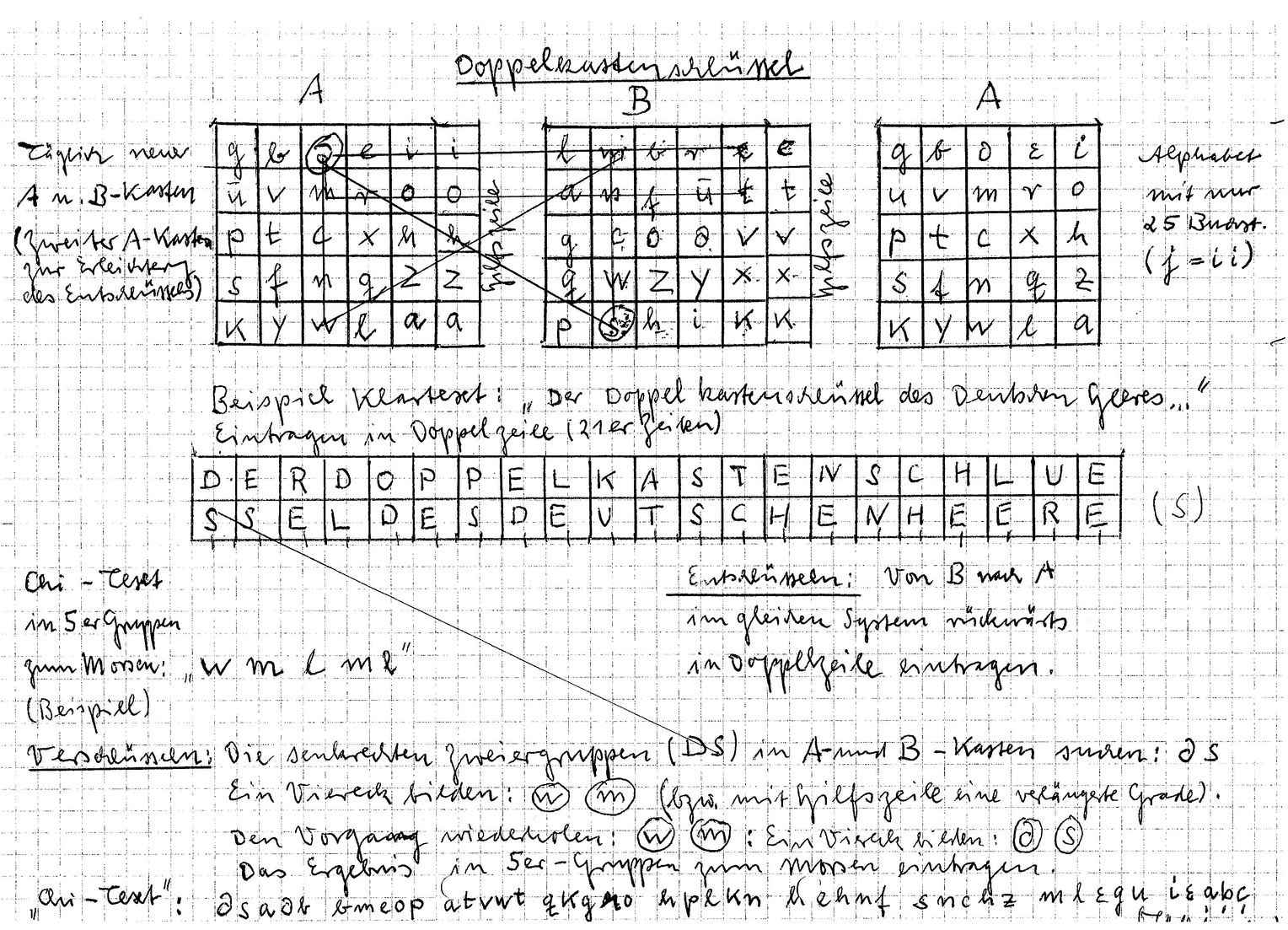
The double box is a variant of the Playfair cipher. As has been pointed out on this blog many times before, the Playfair uses a permutation of the alphabet (without the J) as the key, written in a 5×5 matrix. The double box requires even two matrices of this kind, as in the following example:
MUEZC QAKGD KGQAD MZCUE RTBSY FHVLO FOHVL INPWX PWINX TBSRY
The double-box varaint I introduced in my recent article is the most basic one. Letters are encrypted pair-wise, based on two substitution rules. Both require that the first letter of a pair is chosen in the first matrix, while the second letter is located in the second matrix. For instance, the letter pair TC is selected from the matrices as follows:
MUEZC QAKGD KGQAD MZCUE RTBSY FHVLO FOHVL INPWX PWINX TBSRY
Depending on the position of the letters, one of the following two rules is applied:
Rule 1: If the two letters of a pair are not in the same line, the first one is encrypted to the letter in the second table standing in the same line as the first letter and in the same column as the second letter. The second letter is encrypted to the letter in the first table standing in the same line as the second letter and the same column as the first letter.
As an example, TC is encrypted to VG:
MUEZC QAKGD KGQAD MZCUE RTBSY FHVLO FOHVL INPWX PWINX TBSRY
Rule 2: If the two letters are in the same line, the first letter is encrypyted to the right neighbor of the second one and the second one is encrypted to the right neighbor of the first one (the first column of each matrix is considered the right neighbor of the fifth).
As an example, VX is encrypted to IL:
MUEZC QAKGD KGQAD MZCUE RTBSY FHVLO FOHVL INPWX PWINX TBSRY
The description of this double box variant is taken from the German Wikipedia entry. In Friedrich Bauer’s book Decrypted Secrets, a slightly different version is described. In rule 1, this variant changes the order of the ciphertext pair. TC is not encrypted to VG, but to GV. This is consistent with the double-box description WW2 veteran Jürgen Reinhold provided me.
All three sources mention that the plaintext pairs were not (or not necessarily) chosen in the obvious way (TH IS IS AN EX AM PL EX), but based on digraphs generated from different lines. In the following case, the pairs would be TS HA IN SE IX AL ME PX:
THISI SANEX AMP LEX
Reinhold used a line length of 21 for generating the pairs. The same is mentioned on Wikipedia. Bauer doesn’t mention the line length.
According to a double box variant described on Oliver Kuhlemann’s website, the result of the first digraph substitution is substituted a second time. This only makes sense if the letter from the second matrix is taken first (as in the variant described on Wikipedia). In our example, TC is mapped to VG (first substitution), then VG is mapped to WZ (second substitution). This means that TC is encrypted to WZ.
Frode Weierud’s double-box cryptograms
After publication of my article, Frode Weierud, …
… one of the world’s leading Enigma and WW2 cipher experts, told me that he had found a number of original double-box messages from the German Police (Ordnungspolizei) in Second World War. He thankfully provided me scans an transcripts of all of these.
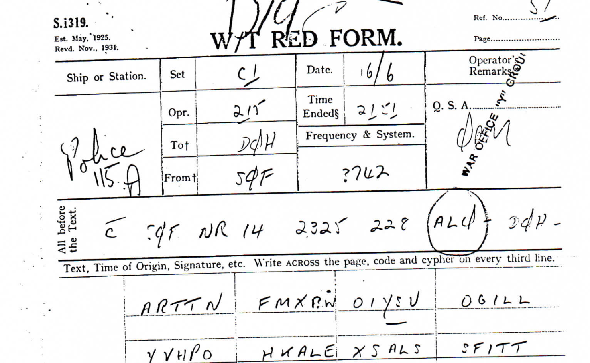
The first message Frode informed me about was sent by the station SQF (Mogilev1) to the station ALQ via DQH (Berlin) on 16 June 1942. The message was transmitted on the night frequency of the Russia high
frequency (HF) network at 3742 kHz2.
The first ciphertext group, here ARTTN, is the discriminator group for the double-box key used. The discriminator is the last three letters, TTN, which can be in any order, such as TNT, NTT etc. Four such discriminators were allocated to each daily key. The discriminator is not part of the message and it must therefore be removed before deciphering the message.
BMRA115/16/42 2151/16/3742 POLICE DQH V SQF C' SQF NR14 2325 228 ALQ DQH ARTTN FMXBW OIYSU OGILL YVHPO HKALE XSALS SFITT EDSPG HGCGP VHTVL LMCIA LWTIF FMRSG HFDAT VTDRV SPTVR VSYSE FYABL SCKQU ECCZR EQUOT TGTOA VWYAB NOMMY AXBTI TUVHQ BIDKO HVQWU ZVXVQ RORAE XQETV GIEOX KCDDA DRCLL NTZHN BEVRU XEDGA EFYVV PDBZA VXRPV QXSLW BCWYK NZKVV HNUOL PLI ++ ( QRM ) CTN 1/3 OIYSU 2/1 EDSPG 2/6 FMRSG 3/4 SCKQU 3/6 EQUOT 5/6 XEDGA TS 2249 MIC
The message is a transcript of the attached teleprinter message sent from the English intercept service (Y-service) to Bletchley Park for analysis and decoding. The message was intercepted by two different intercept stations and the corresponding Red Forms from stations No. 51 and 43 have also been attached. Here it can been seen that some of the letters have been received differently probably due to a weak signal from the transmitting station and as mentioned, due to noise and interference (QRM).
The following five double-box messages (several of them composed of two parts) were sent by German Police in WW2, too. Four of the texts are from the same day, 27 February 1942. The first message, …
… dated 28 February 1943, might be from the same date. The indicator, XOS, is the same as for some of the other messages.
BMRC43/28/2/43 0827/28/6645 POLICE SRS V SRS1 C' SRS1 NR4 0530 2TLE 1TL 143 SRS SRXOS ZMOLP CSMEO SXISF SEIQW QRMKV ILTXV VMETC SSMNL GAFGL VHGWA LLMSO GWMUV YGGUM SEZFV FMVYF TEIL2 WFYZI DFSRI CWLAG YQDMR OIBXB KLSOR BNNME QARGH GXORN XKZIT RYCZH IMN ++ 2TL SWAMPED QRM BMRD33/27/2/42 0941/27/6890 POLICE SRS1 V DQH C' BERLIN NR 4 1015 79 SRS9 KFWOJ PXSXH IHVGD OLIXA DYZZT RFBLQ XPLPN MSLSB ZZSFP GHNHI RRRAF KVUVV MLDWW TMLVV ZRSFP QDSU ++ BMRD34/27/2/42 1310/27/6890 POLICE SQF V DSO C' DSO NR 11 1030 2TLE 1TL 165 SQF DNOSX HYUPD DDLSO RFKZM KNLTB SCNLF PNXIN UTNAA ADOHA MZVGA LAGOI BGXMO FZDBT FVNMN IZFIP GUIZQ WVMKF FPYXH NLVLM LSIRM CLLGL UUEZO GELNF LKFPS NCSVM OVKZX RIRMS SNZHM SAPNU LZXPB KXWAF ORUIU ILCSA ++ 2TL 91 0913 DRANR RNXRG CASFU FMYPF PPDAE RMOGV CORDH VNFVX NMKSV DTAFX PNMZZ QHKMP HTUEQ TPSYY LOMAT GPHII AFSUM NGWZL B ++ BMRE72/27/2/42 1446/27/6645 (POLICE) (31) SRS3 V SRS1 SRS2 NR2 1120 2TLE 1TL 183 SRS3 SBWYY CCILC DGAFS PDSAT FBNVM DROLG XOWMY FMAPT TUYFY ZZXSY SAOTZ NHEQF MXOAS IIOQF SPMZC BXGHA ZUPDD AEGMO EVQYQ GKTVZ ZVLNV APPLP QLZFG MSLZC OELQD SNZIZ VMSOG FGGXO PUTUQ KXSWA SCTLC KSMNP TAGVL LCVML MBFES COPXS GYO ++ 2TL 149 (1450) (31B) LENRA RESCD OMTWV HMCZP POROM VLMRT VRERU VZT.. MPRLV FMOVR NSVDU FSNXN VORLN BRYPN MXPDD UZOLN VSZLO FGNMD HORGX LNOLO GISNF UPZZF KBLKE NTEZU FKCOL VLLKS CQKLL KNELC TKVPE XNME ++ BMRD67/27/2/42 1455/27/6645 POLICE SRS3 V SRS1 SRS2 NR3 1130 2TLE 1TL 175 - SRS3- OWQWJ OPORP CVPMR CNHDI HEQQC HFKFE QNLXP MSESQ DESMO SCMEF PUKTV VITFL NWMSG ZAVGQ LFSQD XNMSM NAPMS LDMMD DBQOL UFPQO IAFIL CBVZS DZZBX PQYLY AFSRP PEMSP LDDZG HMQZO IIXKO PCORL ZVMIP ATEKZ RMSPM ALAPM SQXLV +++ CTN 2/6 ZAVGO 4/6 PCORL ALT 5/2 ALXPM [Editor: This group is ALAPM or ALXPM] 2TL 163 (1457) WNSXO EQUMV HLNPC TBMIL VBFSA FSEQX XFELY TCMQV YFAIR UVORN NAPOR RPPRM SMEIX LGTMO IQZFP IPLKI RBFIR GUGDW NOSTV NMYLC TMTOM OMIOF GNMEQ MREEI IWFYY RXCOO RHYLQ VMGOL LCIHE ORRKK NXGSS MSMTC VKE +++
Now, the question is if these double box cryptograms can be broken. In my view, it should be possible, as most messages Are much longer than a hundred letters and as some of them are probably encrypted with the same key. A well-designed hill climbing program should be able to solve ciphertexts of this kind.
However, we don’t know how exactly the double box variant used in this case worked. My first guess would be that the version with two substitution steps and digraphs generated with 21-letter lines was employed, but this is far from sure.
Can a reader break these cryptograms anyway?
Follow @KlausSchmeh
Further reading: Who was Harry Welsch?
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/





Kommentare (5)