Der Schweizer Mathematiker Leonhard Euler (1707-1783) hinterließ einen verschlüsselten Text. Erst 1953 wurde er gelöst.
Zu den schönen Dingen der Kryptologie-Geschichte gehört, dass man immer wieder nette Überraschungen erlebt. Von einer davon berichte ich heute.
Leonhard Eulers Verschlüsselung
Mir war bis vor Kurzem nicht bekannt, dass der berühmte Schweizer Mathematiker Leonhard Euler (1707-1783) sich mit Verschlüsselung beschäftigt hat. Erst recht wusste ich nicht, dass Euler ein Verschlüsselungsrätsel geschaffen hat, das erst zwei Jahrhunderte nach seinem Tod gelöst wurde. Das war eine echte Überraschung für mich.
Quelle/Source: Wikimedia Commons
In der mir bekannten Literatur wird das Euler-Kryptogramm nicht erwähnt. Dabei ist Leonhard Euler jedem Kryptologen bekannt, denn eine seiner Arbeiten (Satz von Euler) bildet eine wichtige Grundlage des RSA-Verfahrens.
Gestoßen bin ich auf das Euler-Kryptogram über die Webseite Chronicling America, über die ein US-Zeitungsarchiv kostenlos zugänglich ist (danke an Blogleser Schorsch für diesen Tipp). Im Chapel Hill Weekly vom 27.11.1963 fand sich ein Artikel zu Eulers Verschlüsselungsrätsel. Auf der Website der Universitätsbibliothek Göttingen gibt es eine wissenschaftliche Arbeit dazu. Diese wurde von Hans Rohrbach verfasst, einem Mathematiker, der im Zweiten Weltkrieg als Kryptologe arbeitete.
Das Logogryphum
Euler bezeichnete sein Kryptogramm als “Logogryphum”. Er erstellte es für seinen Kollegen Christian Goldbach (1690-1764), dem er es per Brief zuschickte. Auch Christian Goldbach ist ein bekannter Name, wenn auch nicht in der Kryptologie. Nach ihm ist die Goldbachsche Vermutung (“jede gerade Zahl größer 2 ist Summe zweier Primzahlen”) benannt, eines der bekanntesten ungelösten Probleme der Mathematik.
Euler schrieb folgende Zeilen an Goldbach:
Ich habe vor einiger Zeit nachfolgenden logogryphum entworfen, worin alle characteres Buchstaben bedeuten und der Text latein ist:
Quelle/Source: Rohrbach
Ungeachtet hier die Bedeutung der characterum nicht veränderlich ist, so deucht mich doch, daß dergleichen Schrift nicht leicht dechiffriert werden kann.
Die Reaktion Goldbachs auf dieses Rätsel ist nicht bekannt. In der Korrespondenz zwischen ihm und Euler wird es nicht mehr erwähnt. Die Lösung blieb vorläufig unbekannt.
Die Lösung
1907 rief ein “Euler-Kommittee” (ich vermute, diese Organisation ist mit der heute noch existierenden Euler-Kommission identisch) einen Wettbewerb ins Leben, der für die Lösung des Logogryphums eine Geldprämie aussetzte.
Erst im Jahr 1953 wurde das Logogryphum endlich dechiffriert (ob die Geldprämie ausbezahlt wurde, ist mir leider nichtbekannt). Ein gewisser Pierre Speziali veröffentlichte die Lösung als erster, der besagte Hans Rohrbach fand sie kurz danach ebenfalls und unabhängig davon.
Eulers Aussage “die Bedeutung der characterum nicht veränderlich ist” deutete darauf hin, dass er eine monoalphabetische Substitution verwendet hatte. Die Klartextsprache gab Euler als Latein an. Eine der Schwierigkeiten bestand darin, dass der Geheimtext keine Leerzeichen enthält. Wie man ein solches Kryptogramm löst, steht in meinem neuen Buch Codebreaking: A Practical Guide.
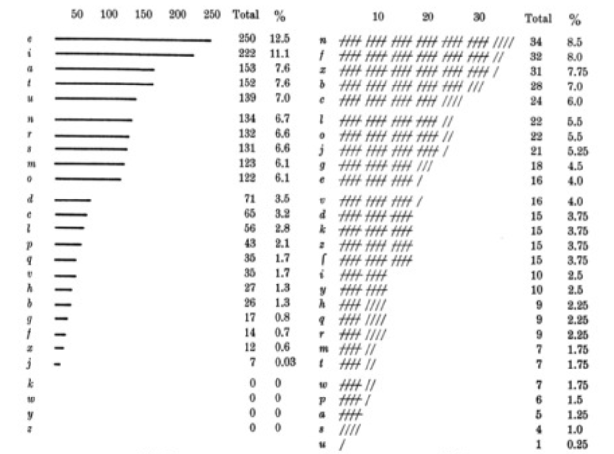
Rohrbach wusste auch ohne diese Literaturquelle, wie er vorgehen musste. Er fertigte zunächste eine Häufigkeitsanalyse an. Das folgende Bild zeigt den Vergleich zwischen der lateinischen Sprache (links) und dem Geheimtext (rechts):
Quelle/Source: Rohrbach
Wie man sieht, kommen im Geheimtext fünf Buchstaben mehr vor als im lateinischen Alphabet. Dabei handelt es sich um die Buchtaben K, W, Y und Z (deren Häufigkeit ist in der Abbildung mit 0 angegeben) sowie eine Version des S, die aussieht wie ein “f” ohne Querstrich. Die Häufigkeitsverteilung ist im Geheimtext etwas flacher als in der lateinischen Sprache. Rohrbach vermutete, dass Euler Homophone (mehrere Geheimtextbuchstaben mit gleicher Bedeutung) verwendet hatte.
Verschlüsselungsverfahren mit Homophonen (auch als “homophone Chiffren” bezeichnet) sind oftmals schwierig zu lösen. Das vor Kurzem gelöste zweite Zodiac-Kryptogramm ist ein Beispiel dafür. Zum Glück für Rohrbach gab es in diesem Fall nur fünf überschüssige Buchstaben, was auf fünf Homophone hindeutete. Andere Geheimtexte enthalten deutlich mehr.
Rohrbach untersuchte nun Buchstabengruppen, die häufiger im Text vorkommen. Dabei verglich er auch ähnliche Gruppen – beispielsweise XOKF und KOXF. Durch derartige Vergleiche kam er zum Schluss, dass die fünf Paare J/F, K/X, W/T, Y/G und Z/R Homophone bilden, also für den gleichen Klartextbuchstaben stehen.
Als nächstes untersuchte Rohrbach die Häufigkeiten von Buchstabenpaaren (Bigrammen). Im Lateinischen ist der Buchstabe Q relativ häufig und steht immer vor einem U. Rohrbach suchte daher nach einem häufigen Bigramm, dessen erster Buchstabe nur in Kombination mit einem bestimmten anderen auftritt. Ein deratiges Paar fand er jedoch nicht. Er schloss daraus, dass Euler für QU einen einzelnen Geheimtextbuchstaben verwendet hatte.
Im Lateinischen gibt es nur vier Buchstaben, die nach einem QU stehen können: A, E, I und O. Alle vier sind relativ häufig. Mit dieser Überlegung und einem Blick auf die Bigramm-Häufigkeiten konnte Rohrbach die fünf Buchstaben Q[U], A, E, I und O identifizieren.
Der Rest war Routinearbeit. Mithilfe der fünf identifizierten Buchstaben ließen sich Wörter und dadurch weitere Buchstaben erraten.
So ermittelte Rohrbach folgende Ersetzungstabelle:
Quelle/Source: Rohrbach
Nun erkennt man, dass Euler für die Klartext-Buchstaben A, E, I/J, N, O und R Homophone verwendet hat. Da Euler zwischen I und J nicht unterschied (was im Lateinischen üblich ist), ergaben sich sechs statt der erwarteten fünf Homophone.
Leider gibt Rohrbach den Klartext nicht direkt an (vielleicht hat ein Leser Lust, diesen zu erstellen), sondern nennt nur eine überarbeitete Klartextversion, in der Fehler und Auslassungen korrigiert sind:
Quelle/Source: Rohrbach
Dieser Text stammt aus Caesars Bellum Gallicum.
Heute würde man ein solches Kryptogramm wohl mit einem Computer und Hill Climbing lösen. Hans Rohrbach hat gezeigt, dass es auch von Hand geht.
Follow @KlausSchmeh
Further reading: Wie ein Mathematiker einen Geheimcode aus dem Nachlass von US-Präsident Jefferson knackte
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/
Kommentare (6)