An encrypted text by mathematician Leonhard Euler
The Swiss mathematician Leonhard Euler (1707-1783) left behind a coded text. It was not solved until 1953.
One of the nice things about cryptology is that you always get nice surprises. I report on one of them today.
Leonhard Euler’s Encryption
Until recently, I was not aware that the famous Swiss mathematician Leonhard Euler (1707-1783) was involved with encryption. Even more so, I did not know that Euler created an encryption puzzle that was not solved until two centuries after his death. That was a real surprise for me.
The Euler cryptogram is not mentioned in the literature known to me. But Leonhard Euler is known to every cryptologist, because one of his works (Euler’s theorem) is an important basis of the RSA method.
I came across the Euler cryptogram via the website Chronicling America, which provides free access to a US newspaper archive (thanks to blog reader Schorsch for this tip). In the Chapel Hill Weekly of 11/27/1963 there was an article on Euler’s cryptogram. On the website of the University Library of Göttingen there is a scientific paper about it. This was written by Hans Rohrbach, a mathematician who worked as a cryptologist during World War II.
The logogryphum
Euler called his cryptogram a “logogryphum”. He created it for his colleague Christian Goldbach (1690-1764), to whom he sent it by letter. Christian Goldbach is also a well-known name, although not in cryptology. Goldbach’s conjecture (“every even number greater than 2 is the sum of two prime numbers”), one of the most famous unsolved problems in mathematics, is named after him.
Euler wrote the following lines to Goldbach:
I have designed some time ago subsequent logogryphum, where all characteres mean letters and the text is Latin:
Goldbach’s reaction to this puzzle is not known. It is not mentioned again in the correspondence between him and Euler. The solution remained unknown for the time being.
Although the meaning of the characterum is not variable here, it seems to me that such writing cannot be easily deciphered.
Die Reaktion Goldbachs auf dieses Rätsel ist nicht bekannt. In der Korrespondenz zwischen ihm und Euler wird es nicht mehr erwähnt. Die Lösung blieb vorläufig unbekannt.
The solution
In 1907, an “Euler Committee” (I assume that this organization is identical with the Euler Commission which still exists today) started a competition which offered a cash reward for the solution of the logogryph.
It was not until 1953 that the logogryphon was finally deciphered (whether the money was paid out is not known to me). A certain Pierre Speziali was the first to publish the solution, the aforementioned Hans Rohrbach also found it shortly afterwards and independently.
Euler’s statement “the meaning of characterum is not mutable” indicated that he had used a monoalphabetic substitution. Euler gave the plaintext language as Latin. One of the difficulties was that the ciphertext did not contain any spaces. How to solve such a cryptogram is in my new book Codebreaking: A Practical Guide.
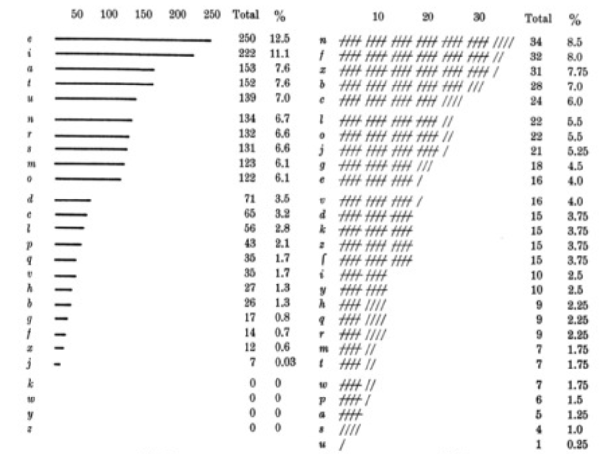
Rohrbach knew how to proceed even without this literature source. He first made a frequency analysis. The following picture shows the comparison between the Latin language (left) and the ciphertext (right):
As you can see, there are five more letters in the ciphertext than in the Latin alphabet. These are the letters K, W, Y and Z (their frequency is given as 0 in the figure) as well as a version of S, which looks like an “f” without a slash. The frequency distribution is somewhat flatter in ciphertext than in Latin. Rohrbach suspected that Euler had used homophones (several ciphertext letters with the same meaning).
Encryption schemes using homophones (also called “homophonic ciphers”) are often difficult to solve. The recently solved second Zodiac cryptogram is a case in point. Fortunately for Rohrbach, there were only five excess letters in this case, indicating five homophones. Other ciphertexts contain significantly more.
Rohrbach now examined groups of letters that occur more frequently in the text. He also compared similar groups – for example XOKF and KOXF. Through such comparisons, he concluded that the five pairs J/F, K/X, W/T, Y/G, and Z/R form homophones, i.e., stand for the same plaintext letter.
Next, Rohrbach examined the frequencies of pairs of letters (bigrams). In Latin, the letter Q is relatively common and always precedes a U. Rohrbach therefore looked for a frequent bigram whose first letter occurs only in combination with a certain other. However, he did not find such a pair. He concluded that Euler had used a single ciphertext letter for QU.
In Latin, there are only four letters that can come after a QU: A, E, I, and O. All four are relatively common. With this consideration and a look at the bigram frequencies, Rohrbach was able to identify the five letters Q[U], A, E, I and O.
The rest was routine work. With the help of the five identified letters, words and thus other letters could be guessed.
Thus Rohrbach determined the following substitution table:
Now we see that Euler used homophones for the plaintext letters A, E, I/J, N, O and R. Since Euler did not distinguish between I and J (which is common in Latin), this resulted in six homophones instead of the expected five.
Unfortunately, Rohrbach does not give the plaintext directly (perhaps a reader would like to provide it), but only gives a revised plaintext version in which errors and omissions are corrected:
This text comes from Caesar’s Bellum Gallicum.
Today, such a cryptogram would probably be solved with a computer and hill climbing. Hans Rohrbach has shown that it can also be done by hand.
Follow @KlausSchmeh
Further reading: Wie ein Mathematiker einen Geheimcode aus dem Nachlass von US-Präsident Jefferson knackte
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/







Letzte Kommentare