Im Jahr 1920 ließ der deutsche Textilingenieur Rudolf Zschweigert eine Verschlüsselungsmaschine patentieren. Heute stelle ich einen Text vor, der mit dieser verschlüsselt wurde. Kann ein Leser sie lösen?
English version (translated with DeepL)
Letztes Jahr habe ich für die HistoCrypt einen Beitrag über die Verschlüsselungsmaschine von Rudolf Zschweigert eingereicht. Diese Arbeit wurde zwar angenommen und ist dann im Konferenzband erschienen, doch die Veranstaltung selbst ist Corona-bedingt ausgefallen. Den geplanten Vortrag über das besagte Gerät konnte ich daher nicht halten.
Am kommenden Samstag (20. März 2021) habe ich die Gelegenheit, die abgesagte Präsentation nachzuholen, und zwar als Webinar im Rahmen der International Conference on Cryptologic History (ICCH). Es handelt sich bereits um meinem siebten Vortrag in dieser Reihe. Er findet dieses Mal um 17 Uhr (also eine Stunde früher als sonst) statt und ist (wie immer) kostenlos. Die Zugangsdaten werden über die Mailing-Liste verschickt, die man auf der ICCH-Webseite abonnieren kann. Wer dieses Abo nicht will, kann mir gerne eine Mail schicken, dann lasse ich ihm/ihr den Link zukommen.
Mein Partner bei diesem Vortrag ist der Brite Jerry McCarthy, über den ich auf Cipherbrain bereits mehrfach berichtet habe. Jerry hat unter anderem die Enigma-Knackmaschine “Zyklometer” nachgebaut.
Der Zschweigert-Kryptograf
Die von Zschweigert entwickelte Verschlüsselungsmaschine (Zschweigert-Kryptograf) ist einer der vielen Chiffriermaschinenentwürfe, die in den Jahren nach dem Ersten Weltkrieg (1914-1918) entstanden sind. Zschweigert war ein Textilingenieur, der zuvor Näh- und Webmaschinen konstruiert hatte, wovon weitere Patente zeugen, und dabei offenbar auf die Idee kam, ein Chiffriergerät zu bauen.
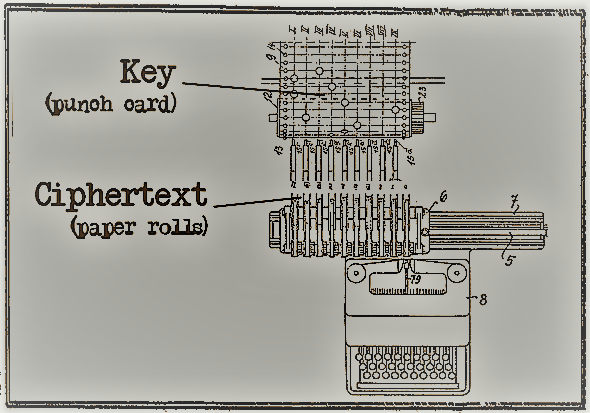
Anders als die Enigma und so gut wie alle anderen mechanischen Kryptogeräte realisiert der Zschweigert-Kryptograph eine Transpositions-Chiffre, und nicht etwa eine Substitutions-Chiffre. Buchstaben werden hier also nicht ersetzt, sondern in der Reihenfolge vertauscht.
Die Zschweigert-Maschine arbeitete mit neun parallelen Papierrollen. Der Schlüssel wurde auf einer neunspaltigen Lochkarte bereitgestellt. Die Zahl der Lochreihen war beliebig. Pro Reihe gab es genau ein Loch. Die Maschine arbeitete den Klartext Buchstabe für Buchstabe durch und sprang dabei jeweils eine Reihe auf der Lochkarte weiter. Die Spalte, in der sich das Loch befand legte fest, auf welche Rolle gedruckt wurde. War die Maschine in der letzten Reihe angekommen, dann sprang sie anschließend wieder an den Anfang.
Das folgende Video zeigt, wie die Maschine funktionierte (die Lochkarte hat hier fünf Reihen):
Wer es genauer wissen will, kann meine HistoCrypt-Arbeit oder das Patent aus dem Jahr 1920 durchlesen. Dieses Patent ist die einzige mir bekannte Quelle zum Zschweigert-Kryptografen. Im Internet habe ich zwar weitere Informationen zu Rudolf Zschweigert und dessen Unternehmen gefunden, doch die Maschine wird nirgends erwähnt. Es ist zwar möglich, dass sie gebaut wurde (als Prototyp), ich gehe aber davon aus, dass sie nie in der Praxis eingesetzt wurde.
Jerrys Zschweigert-Simulation
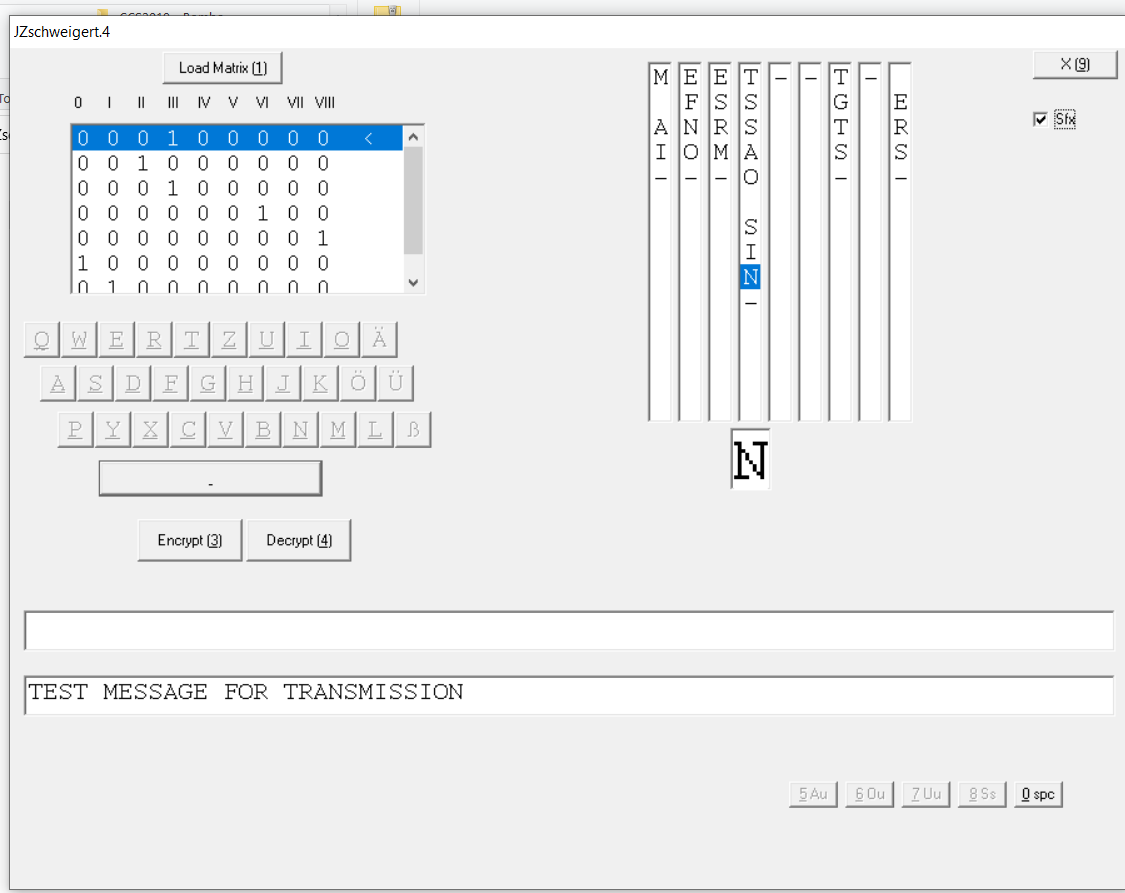
Der besagte Jerry McCarthy hat auf Basis meiner HistoCrypt-Arbeit eine Computer-Simulation des Zschweigert-Kryptografen programmiert. Hier ist ein Screenshot:
Im Vortrag am Samstag wird Jerry diese Software vorstellen.
Eine Challenge
Wie sicher der Zschweigert-Kryptograf ist, hängt vor allem von der Schlüssellänge ab. Diese wird von der Anzahl der Reihen der Lochkarte festgelegt. Im Video hat diese Karte nur fünf Reihen, was recht knapp bemessen ist. Es sollte jedoch möglich sein, auch deutlich längere Lochkarten einzusetzen.
Um etwas mehr über die Sicherheit dieses Geräts herauszufinden, habe ich eine Challenge erstellt. Ich habe zu diesem Zweck einen englischen Text mit knapp über 100 Buchstaben mit dem Verfahren des Zschweigert-Kryptografen verschlüsselt. Das Ergebnis sieht wie folgt aus:
Spaltenweise ausgelesen erhält man folgenden Geheimtext:
EAEA-BTABOASIIE-MOCNSTSMLLNIWSNNICE-RYTKSNHTERYTTWKHPPH-YHWTYIFRR-NTIOOKACNHCGIATR-DLTRDOTS-EOOREPEDNCAN-CPIECPRI
Die Anzahl der Reihen auf der Lochkarte ist Teil des Schlüssels.
Kann ein Leser dieses Kryptogramm knacken? Falls es jemandem bis zum kommenden Samstag gelingt, werde ich dies natürlich im Vortrag erwähnen.
Follow @KlausSchmeh
Further reading: Prince Edward opens new exhibition at Bletchley Park
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/





Kommentare (10)