Im Zusammenhang mit der Post-Quanten-Kryptografie spielt das Problem der gekreuzten Leitern eine Rolle. Es ist einfach zu erklären, aber nur schwer zu lösen.
English version (translated with DeepL)
Vor über 20 Jahren unterhielt ich mich mit dem inzwischen leider verstorbenen Kryptologen Prof. Hans Dobbertin. Wir kamen eher zufällig auf eine mathematische Knobelei zu sprechen, die ich kurz zuvor mit einigen Seminarteilnehmern zum Wiedereinstieg nach der Mittagspause (zur Überwindung des “Suppenkomas”) diskutiert hatte.
Es ging um das Problem der gekreuzten Leitern. Dies ist eine mathematische Fragestellung, die scheinbar ein Mittelstufenschüler lösen kann – mit dem Strahlensatz und dem Satz des Pythagoras. Doch was recht einfach aussieht, entpuppt sich als nahezu unlösbar. Von mehreren Dutzend Seminarteilnehmern, denen ich die Knobelei damals vorstellte, konnte sie keiner lösen. Dabei waren sogar Mathematiker unter den Teilnehmern.
Hans Dobbertin blickte jedoch nur einmal kurz auf das Rätsel und sagte: “Ich weiß, wie es geht! Solche Fragestellungen spielen für bestimmte Krypto-Verfahren eine Rolle, mit denen ich gerade zu tun habe.”
Leider kamen wir nicht mehr dazu, die Sache zu vertiefen. Ich ging aber davon aus, dass Dobbertin, der wohl bedeutendste deutsche Kryptologe überhaupt, keinen Unsinn erzählt hatte. Einige Jahre später wurde mir dann auch klar, was er damals im Sinn gehabt hatte.
Das Problem der gekreuzten Leitern
Fangen wir mit dem Problem der gekreuzten Leitern an. Es wird auch als “Leiterproblem” bezeichnet, was aber missverständlich ist, denn es gibt in der Mathematik mehrere Fragestellungen, die sich um Leitern drehen, wie man hier nachlesen kann.
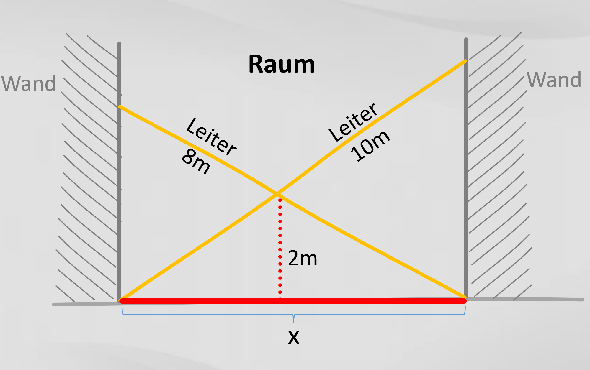
Das Problem der gekreuzten Leitern ist in der folgenden Grafik dargestellt (die angegeben Zahlen sind natürlich nur Beispiele):
Gegeben sind also zwei Leitern in einem Raum, die sich kreuzen. Die Längen der Leitern sowie die Höhe des Kreuzungspunkts sind bekannt. Die Frage ist: Wie breit ist der Raum?
Wie löst man das Problem?
Um die Frage zu beantworten, kann man mithilfe des Strahlensatzes und des Satzes von Pythagoras drei Gleichungen aufstellen. Nach meinen Berechnungen sehen diese so aus:
Die Frage ist nun, wie man dieses Gleichungssystem löst. Mit dem Gauß-Algorithmus kommt man nicht weit. Hans Dobbertin meinte jedoch, dass es eine andere Methode gäbe. Er dachte wahrscheinlich an so genannte Gröbner-Basen, denn diese spielen in der Post-Quanten-Kryptografie eine Rolle (siehe unten).
Leider bin ich nie dazu gekommen, mich mit Gröbner-Basen zu beschäftigen. Kann ein Leser hier eine verständliche Erklärung liefern und sagen, wie man diese für die Lösung des Problems nutzt?
In der englischsprachigen Wikipedia gibt es einen eigenen Eintrag zum Problem der gekreuzten Leitern. Dort werden mehrere Lösungswege diskutiert. Kann ein Leser damit die hier vorgestellte Version lösen?
Vermutlich kann man für diesen Zweck auch eine Mathematik-Software nutzen, die Gleichungssysteme löst. Wolfram Alpha wäre wohl eine Möglichkeit. Hat ein Leser Erfahrung damit?
Anwendung in der Post-Quanten-Kryptografie
Bleibt noch die Frage, welchen Zusammenhang zwischen dem Problem der gekreuzten Leitern und der modernen Kryptografie Hans Dobbertin damals gesehen hat.
Auch hier kenne ich inzwischen die Antwort: Das obige Gleichungssystem zählt zu den multivariaten Gleichungssystemen. Diese wiederum sind die Grundlage der multivariaten Kryptografie, die zur asymmetrischen Kryptografie gehört.
Zur multivariaten Kryptografie zählen beispielsweise “Oil and Vinegar”-Signaturen – benannt nach Variablen, die man als “Ölvariablen” und “Essigvariablen” bezeichnet. Die multivariate Kryptografie wird zur Post-Quanten-Kryptografie gezählt. Die damit realisierbaren digitalen Signaturen lassen sich also selbst mit einem Quantencomputer nicht fälschen.
Die multivariate Kryptografie basiert darauf, dass multivariate Gleichungssysteme einfach zu konstruieren, aber schwer zu lösen sind. Die beste bekannte Lösungsmethode nutzt die erwähnten Gröbner-Basen. Dieses Verfahren ist jedoch so aufwendig, dass man bei größeren Gleichungssystemen selbst mit dem besten Rechner einige Jahrmilliarden benötigt.
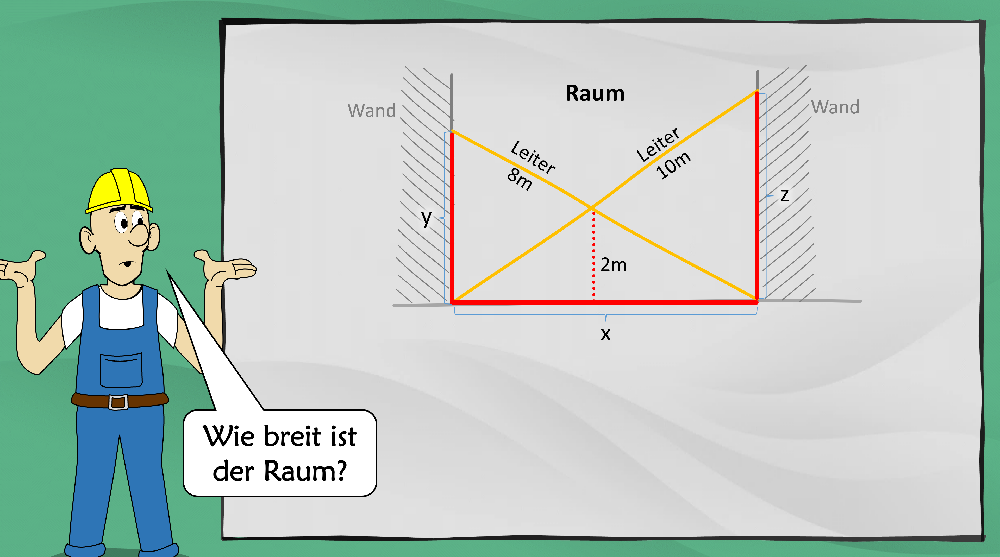
Ich habe inzwischen zahlreiche Vorträge gehalten, in denen ich multivariate Kryptografie (und andere Post-Quanten-Verfahren) mithilfe von Cartoons vorstelle. Hier eine Folie, die ich dabei verwende:
Das Problem der gekreuzten Leitern nehme ich dabei immer als Einstieg. Obwohl ich inzwischen schon mindestens ein Dutzend Literaturquellen zur multivariaten Kryptografie durchgearbeitet habe, ist mir das Problem der gekreuzten Leitern in diesem Zusammehang noch nie begegnet. Anscheinend bin ich der einzige, der dieses anschauliche Rätsel für diesen Zweck verwendet.
Kennt ein Leser weitere anschauliche mathematische Fragestellungen, die man mit einem multivariaten Gleichungssystem lösen kann?
Follow @KlausSchmeh
Further reading:
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/




Kommentare (57)