StartseiteCipherbrain

Playfair cipher: Is it unbreakable, if the message has only 50 letters?

Von / 7. April 2018 / 15 Kommentare / Seite 2 von 2 / Auf einer Seite lesen
Mehr

CB FT MH GR IO TS TA UF SB DN WG NI SB RV EF BQ TA BQ RP EF BK SD GM NR PS RF BS UT TD MF EM AB IM

 

How to solve a Playfair encryption

Using a computer, there are two ways to attack a Playfair cipher:

  • Dictionary attack: It is possible to break a Playfair cipher by guessing the keyword. The word SURPRISE is contained in virtually every English dictionary, so a computer that tests one keyword candidate after the other will sooner or later find it.
  • Hill climbing: Hill climbing is the current super-algorithm of historical codebreaking. As George Lasry pointed out, hill climbing (enhanced with simmulated annealing) can break a Playfair cipher of more than 80 letters.

There are several books that explain how a Playfair can be solved without computer support – for instance Helen Fouché Gaines’ Cryptanalysis and André Langie’s Cryptography. The concept is to guess a few words in the cleartext and to derive the 5×5  matrix based on the peculiarities of the Playfair cipher (for instance, if AB->XY then BA->YX). However, breaking a Playfair cryptogram manually is pretty difficult, especially if the ciphertext is short (the examples described in these books refer to messages of several hundred letters). In addition, these books assume that a few words of the cleartext are known. Nevertheless, none of these books describes the complete Playfair codebreaking procedure – instead, most of the trial-and-error reckoning necessary is simply omitted.

 

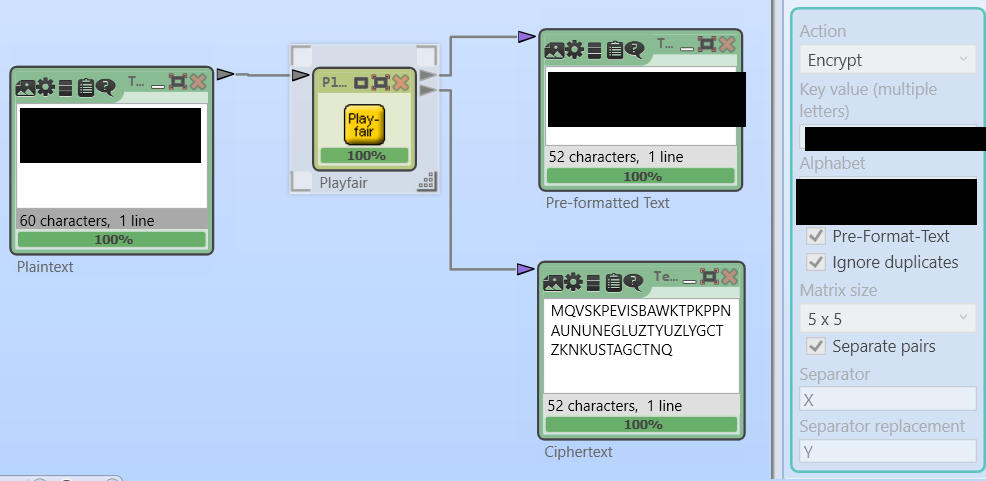
A Playfair challenge

Here is a Playfair-encrypted text I created:

MQVSKPEVISBAWKTPKPPNAUNUNEGLUZTYUZLYGCTZKNKUSTAGCTNQ

Can a reader break this challenge? Here are the details:

  • The cleartext has exactly 50 letters (spaces not included). It is written in English.
  • I used the software CrypTool 2 for encryption. As far as I know, CrypTool implements the Playfair cipher exactly the way it is explained above.

Playfair-Challenge-Cryptool-Screenshot

  • The keyword is a random transposition of the alphabet. So, a dictionary attack won’t work.

As mentioned, this challenge might be a pretty hard one, as the ciphertext is so short. Can a reader solve it anyway?


Further reading: A mird in the hand is worth two in the mush: Solving ciphers with Hill Climbing

Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/

Subscribe to Blog via Email

Enter your email address to subscribe to this blog and receive notifications of new posts by email.

1 / 2
Stichworte:
Mehr

Kommentare (15)

  1. #1 George Lasry
    Israel
    7. April 2018

    @Klaus: Thanks for the challenge. Question: Is the key derived from a sentence/word, or a random square?

    Since your last post on Playfair (and my comment), I have been working on an improved Simulated Annealing version using hexagrams, which seems to give good results, for 60 and above. Let’s see how it performs with 50 🙂

  2. #2 Klaus Schmeh
    7. April 2018

    John Smith via Facebook:
    I was thinking of some attacks that would probably work against this today. Going to write them soon. Thanks for posting.

  3. #3 Klaus Schmeh
    7. April 2018

    @George:
    > Is the key derived from a sentence/word, or a
    >random square?
    The key is a random square. It’s not derived from anything.

  4. #4 George Lasry
    7. April 2018

    @Klaus: I think I am very close :-). Could you kindly verify that in the ciphertext, the pair “IS” is correct. With it, the name of the city is garbled at decryption. I think it should be “UK”. Then the city is decrypted correctly.

  5. #5 Thomas
    7. April 2018

    @Klaus
    Is it right that the plaintext has 50 letters: If I’m not wrong, the ciphertext has 52 letters = 26 bigrams (repetitions: bigrams 3 and 9 (KP) and bigrams 15 and 17 (UZ)).

  6. #6 Klaus Schmeh
    7. April 2018

    @George:
    Yes, IS appears in the cleartext.

  7. #7 Klaus Schmeh
    7. April 2018

    @Thomas:
    >Is it right that the plaintext has 50 letters: If I’m
    >not wrong, the ciphertext has 52 letters
    Yes, the plaintext has 50 letters. CrypTool added two Xs.

  8. #8 George Lasry
    7. April 2018

    @Klaus: Thanks, but I was asking about the ciphertext. According to what I have,
    MQVSKPEVIS….
    should be
    MQVSKPEVUK……
    otherwise, the name of the city is garbled in decryption (it shows a K instead of an R in the name of the city ??K?? instead of ??R??).

    I think I have the solution, just waiting for your confirmation that IS should be replaced with US in the ciphertext.

  9. #9 Klaus Schmeh
    7. April 2018

    @George: I’m afraid, you’re right. Sorry for this mistake.

  10. #10 Thomas
    7. April 2018

    Oh, I see. The cleartext has double letters in two places which had to be split up with “X”, because Playfair cannot encipher double letters in one bigram.

  11. #11 Klaus Schmeh
    7. April 2018

    @Thomas: Yes, either there is a doubled letter or the length of the text is odd.

  12. #12 George Lasry
    7. April 2018

    @Klaus: Many thanks, so I think my solution is correct:

    Key:
    XBHQY
    NKZRE
    LSGFT
    DAOUC
    VIMWP
    WHILEINPARISIRECEIVEDORDERSTOREPORTXTOGENERALFOSTERX

    I obtained a very close solution using Simulated Annealing with fixed temperature, and log hexagrams (6-grams).

    I then manually fixed the errors, and used the correct plaintext as a crib to obtain the correct key.

    But I couldn’t correct the wrong PAKIS to PARIS, unless I changed the ciphertext 🙂

    Thanks for this very interesting challenge!.

  13. #13 Klaus Schmeh
    7. April 2018

    @George: Congratulations! The solution is correct. Sorry for the spelling mistake.
    As it seems, I need to post a new challenge now – perhaps, a Playfair message with 30 letters 😉

  14. #14 Thomas
    7. April 2018

    Congratulations, George!

  15. #15 George Lasry
    7. April 2018

    Many thx!. Maybe 40?