Playfair cipher: Is it unbreakable, if the message has only 50 letters?

The Playfair cipher is an encryption method from the 19th century. Some say that a Playfair-encrypted message of 50 or less letters is still secure today, if the method is used properly. Let’s put this claim to the test.

Designing a purely manual cipher that is both secure and convenient is extremely difficult, if not impossible – especially if such a cipher shall withstand modern cryptanalysis.

The Double Column Transposition (DCT, also known as double cube) is considered one of the best manual ciphers. Blog reader George Lasry has suggested the World War I cipher ADFGVX as another interesting candidate, provided that the second step of this method (a transposition) is carried out twice. Others have designed encryption algorithms that use unsuspicious aids, such as Rubik’s cube encryption and Solitaire (uses a deck of cards). Elsiefour and Handycipher are other new manual cipher designs. However, none of these algorithms is secure and fool-proof at the same time.

The Playfair cipher, a method invented by Charles Wheatstone in the 19th century, is simpler than all the ciphers mentioned above. However, it can be broken with hill climbing, provided that the ciphertext is long enough or that the keyword is not too complex. George Lasry, …

… who is one of the world’s leading experts in breaking historical ciphers, has pointed out that a Playfair message with less than 70-80 characters might be very difficult to break:

So, I  decided to create a Playfair challenge that is shorter than 70-80 characters and to publish it on this blog …

How the Playfair works

The Playfair cipher substitutes letter pairs. So, the cleartext needs to be written as a sequence of letter pairs (the following cleartext is a Shakespeare quote taken from Robert Thouless’ life-after-death experiment):

BA LM OF HU RT MI ND SG RE AT NA TU RE SS EC ON DC OU RS EC HI EF NO UR IS HE RI NL IF ES FE AS T

The Playfair cipher requires that no letter pair consist of two equal letters. Therefore, we add an X between the two Ss:

BA LM OF HU RT MI ND SG RE AT NA TU RE SX SE CO ND CO UR SE CH IE FN OU RI SH ER IN LI FE SF EA ST

If the number of letters in the cleartext was odd, another X would have to be added at the last position, but this is not necessary here. Next, we choose a keyword: SURPRISE. Now, we set up a 5×5 matrix, which starts with the keyword (repeating letters are omitted), followed by the remaining alphabet (I and J are considered equal in order to get an alphabet of 25 letters):

S U R P I
E A B C D
F G H K L
M N O Q T
V W X Y Z

Now, we replace the cleartext letter pairs (BA, LM, OF, HU, …) according to the three Playfair rules. Here are the rules in a diagram:

Here are the same rules as a text (I refer to the letter pair to be replaced as XY):

1. If X and Y are not in the same column and not in the same row (this is the most frequent case), form a rectangle and replace the two letters by the other two corner letters (the upper cleartext letter is replaced by the other upper letter in the rectangle, the lower cleartext letter by the lower one). For instance, LM becomes FT.
2. If the two letters stand in the same row, each one is replaced by its right neighbor. Here, BA becomes CB.
3. If the two letters stand in the same column, each one is replaced by its lower neighbor. In our example, AN becomes GW.

When we apply the Playfair rules on our cleartext with our 5×5 matrix, we get the following ciphertext:

CB FT MH GR IO TS TA UF SB DN WG NI SB RV EF BQ TA BQ RP EF BK SD GM NR PS RF BS UT TD MF EM AB IM

How to solve a Playfair encryption

Using a computer, there are two ways to attack a Playfair cipher:

• Dictionary attack: It is possible to break a Playfair cipher by guessing the keyword. The word SURPRISE is contained in virtually every English dictionary, so a computer that tests one keyword candidate after the other will sooner or later find it.
• Hill climbing: Hill climbing is the current super-algorithm of historical codebreaking. As George Lasry pointed out, hill climbing (enhanced with simmulated annealing) can break a Playfair cipher of more than 80 letters.

There are several books that explain how a Playfair can be solved without computer support – for instance Helen Fouché Gaines’ Cryptanalysis and André Langie’s Cryptography. The concept is to guess a few words in the cleartext and to derive the 5×5  matrix based on the peculiarities of the Playfair cipher (for instance, if AB->XY then BA->YX). However, breaking a Playfair cryptogram manually is pretty difficult, especially if the ciphertext is short (the examples described in these books refer to messages of several hundred letters). In addition, these books assume that a few words of the cleartext are known. Nevertheless, none of these books describes the complete Playfair codebreaking procedure – instead, most of the trial-and-error reckoning necessary is simply omitted.

A Playfair challenge

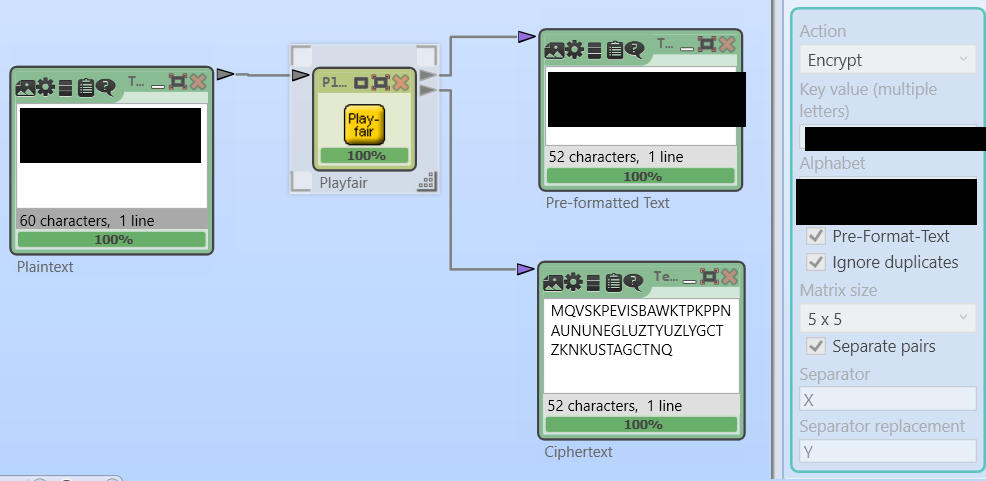
Here is a Playfair-encrypted text I created:

MQVSKPEVISBAWKTPKPPNAUNUNEGLUZTYUZLYGCTZKNKUSTAGCTNQ

Can a reader break this challenge? Here are the details:

• The cleartext has exactly 50 letters (spaces not included). It is written in English.
• I used the software CrypTool 2 for encryption. As far as I know, CrypTool implements the Playfair cipher exactly the way it is explained above.

• The keyword is a random transposition of the alphabet. So, a dictionary attack won’t work.

As mentioned, this challenge might be a pretty hard one, as the ciphertext is so short. Can a reader solve it anyway?
Follow @KlausSchmeh

Further reading: A mird in the hand is worth two in the mush: Solving ciphers with Hill Climbing

Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/