The second encrypted message from the Zodiac Killer is one of the world’s most famous unsolved cryptograms. According to computational linguist Tom Juzek, it will never be solved because no solution exists.
Throughout the late 1960s, the Zodiac Killer, one of history’s most famous unidentified serial murderers, terrorized the San Francisco area in a spree of heinous attacks. He murdered at least five people and seriously injured two. He sent over a dozen taunting letters to the public, in which he boasted about his acts and made fun of the police. The case has never been solved.
The four Zodiac cryptograms
For crypto history enthusiasts, the Zodiac Killer is especially interesting, as four of his letters included encrypted messages. Here’s the first one (it was solved by Donald and Betsy Harden in 1969):
The three other encrypted messages are unsolved to date. Here’s the second message:
This is message #3 (only one line of the letter is encrypted):
And finally, this is the fourth Zodiac cryptogram (two lines encrypted):
———-off-topic————–
For those who speak German, here’s a radio interview I recently gave:
The second Zodiac cryptogram
Messages #3 and #4 are quite short and have a flat letter frequency distribution. This means that the correct solution, it there is one, cannot be distinguished from false ones, which makes these cryptograms virtually unsolvable. For this reason, codebreakers usually focus on the second Zodiac Killer message. As it consists of 340 letters, it is sometimes referred to as Z340.
The first Zodiac message (also known as Z408) proved to be encrypted in a homophonic cipher (this means that a cleartext letter may have several different ciphertext counterparts). As the second cryptogram looks similar to the first, it is reasonable to assume that it was created with the same type of cipher. However, all attempts to find a homophonic substitution table that decrypts Z340 have failed so far. Apparently, the Zodiac Killer, after his first cryptogram had been broken within a short time, tried to make his second try more difficult.
Of course, it is possible that the second Zodiac Killer cryptogram is just a nonsense message (the can be said for the Voynich Manuscript, the McCormick notes, the Debosnys cryptogram and many other unsolved crypto mysteries).
Tom Juzek, a computational linguist, has now published an interesting blog post about Z340 that delivers a number of statistical arguments that support the nonsense hypothesis (thanks to blog reader Ralf Bülow for the hint). This post was published on March 16, 2018. I had never heard of Tom Juzek before. He has never been active in the crypto history community. Perhaps, this will change in the future. I wouldn’t mind seeing works like these at crypto history conferences.
As Juzek correctly states, the letter, bigram and trigram frequencies of Z340 are consistent with a homophonic cryptogram. As an additional statistical tool, Juzek introduces the “mean squared distance from one” (MSD), which is computed for every n-letter-group (ngram) that appears in the cryptogram. The MSD values of a homophonic cryptogram are different from the ones a random sequence over the same alphabet with the same letter frequencies produces.
When checking the MSD values of Z340, Juzek found out: these values stay the same, no matter in which order the letters of the cryptogram are read. Especially, reading Z340 in the usual order renders the same results as reading it backwards or column-wise. This is strong evidence that Z340 is not a homophonic cryptogram. Even if read backwards or column-wise, Z340 does not behave like a real cipher.
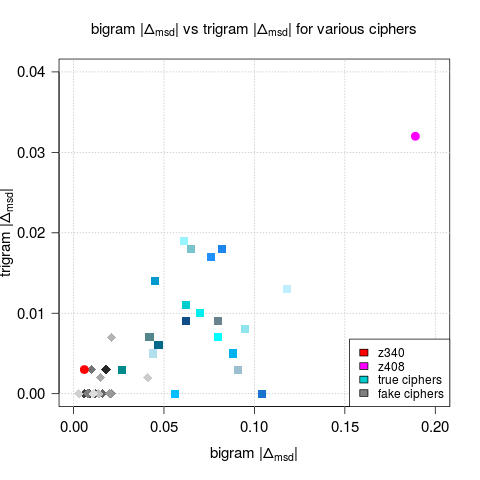
There are a few more statistical analyses Juzek conducts. For instance, he examines a homophonic cipher of his own creation on twenty real texts and twenty random letter sequences. The twenty real texts are taken from sources like one of the non-encrypted Zodiac Killer letters, other letters from serial killers, the book of Genesis and Karl Marx’ The Capital. The twenty random letter sequences were created with a Python script. The cipher Juzek uses is similar to Z408. The following diagram shows the result of this test:
As can be seen, Z340 associates with the fake ciphers. Interestingly, the other true ciphers form their own cluster, away from Z408, implying that the encryption mechanism used for them is a lot stronger than the encryption mechanism of Z408.
A fake or not a fake?
Other tests Juzek describes in his paper strengthen the nonsense hypothesis, too. Nevertheless, Juzek’s work is not a proof that Z340 is a fake cryptogram (and Juzek doesn’t claim that it is). However, Juzek has delivered some interesting evidence that supports the hoax hypothesis.
Generally speaking, the nonsense hypothesis appears to make sense. I can well imagine that the Zodiac Killer wanted to create an unsolvable crypto mystery, after his first encryption had proven weaker than he had expected. Perhaps, to be on the safe side, he decided to create an encrypted message that is unsolvable because there is no solution.
If you follow Juzek’s arguments or if you have a different opinion about Z340, please let me know.
Follow @KlausSchmeh
Further reading: The Zodiac Killer code is solved – at least in this new movie
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/









Kommentare (11)