In the Second World War, the Germans used a manual cipher, the “double box”. Here’s a double-box cryptogram for my readers to solve.
The Doppelkasten-Schlüssel (double box cipher) was one of the most popular encryption systems of the Second World War. Until 1944, this method served as the standard manual cipher in the German military. When an Enigma machine was too expensive, broken, or too heavy to carry, the double box usually was the substitute.
The method
The double box is a variant of the Playfair cipher. As will be shown below, it is even simpler and more elegant than its better-known relative.
As has been explained on this blog many times before, the Playfair cipher uses a permutation of the alphabet (without the J) as the key, written in a 5×5 matrix. The double box requires even two matrices of this kind, as in the following example:
MUEZC QAKGD KGQAD MZCUE RTBSY FHVLO FOHVL INPWX PWINX TBSRY
Letters are now encrypted pair-wise. Contrary to the Playfair cipher, which is based on three substitution rules, the double box needs only two. In both cases, the first letter of a pair is located in the first matrix, the second letter in the second matrix. For instance, the letter pair TC is mapped to the matrices as follows:
MUEZC QAKGD KGQAD MZCUE RTBSY FHVLO FOHVL INPWX PWINX TBSRY
Now, one of the two double-box rules is applied:
Rule 1: If the two letters of a pair are not in the same line, the first one is encrypted to the letter in the second table standing in the same line as the first letter and in the same column as the second letter. The second letter is encrypted to the letter in the first table standing in the same line as the second letter and the same column as the first letter.
As an example, TC is encrypted to VG:
MUEZC QAKGD KGQAD MZCUE RTBSY FHVLO FOHVL INPWX PWINX TBSRY
Rule 2: If the two letters are in the same line, the first letter is encrypyted to the right neighbor of the second one and the second one is encrypted to the right neighbor of the first one (the first column of each matrix is considered the right neighbor of the fifth).
As an example, VX is encrypted to IL:
MUEZC QAKGD KGQAD MZCUE RTBSY FHVLO FOHVL INPWX PWINX TBSRY
That’s it. Contrary to the Playfair cipher, the double box doesn’t require exception handling for identical digraphs.
To make the guessing of message beginnings more difficult, the Germans sometimes generated the digraphs from the plaintext according to the following rule: (letter1, letter22), (letter2, letter23), (letter3, letter24),… In this article, however, I will employ the most obvious way of generating digraphs from a plaintext: (letter1, letter2), (letter3, letter4), (letter5, letter6), …
An example
The message TO BE OR NOT TO BE is written in digraphs as follows (the last X is used for padding):
TO BE OR NO TT OB EX
With the two double box matrices introduced above, the following ciphertext is derived:
FB OQ WW YS FW NW DH
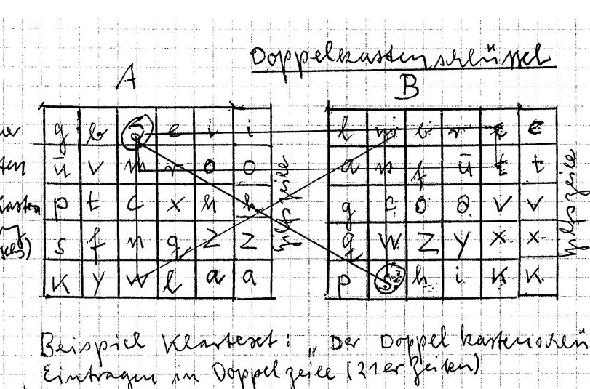
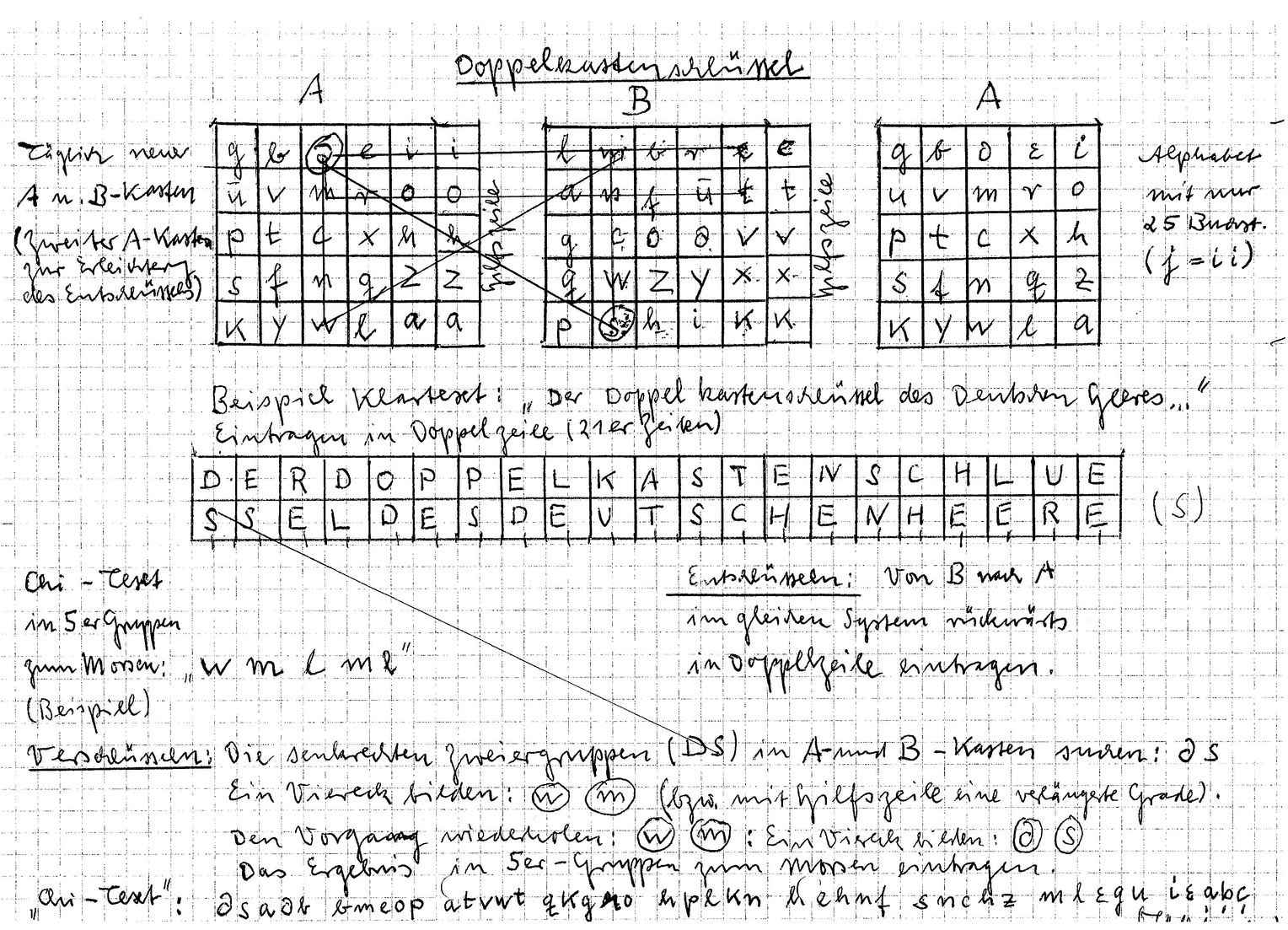
To my regret, I don’t know any original double-box messages from the Second World War, nor any original encryption notes. The closest thing I have is a diagram WW2 veteran Jürgen Reinhold created for me when I interviewed him in 2010:
My book Codeknacker gegen Codemacher contains a chapter about the double box and how it was broken by British cryptanalysts in Bletchley Park.
The only software implementation of the double box I am aware of is available in JCRYPTOOL.
A Challenge
To my knowledge, not much has been published about breaking the double box with modern means. To stimulate research in this area, I have created the following challenge cryptogram:
PW SX SV RM KP IB KL UZ SQ HO KL PV UZ GR ZV PA IV BZ QV SZ HH KI ZT QT MC MT YI HF NV UM IO DZ AA GI UO VV XH RM OT CD ZU LV SF TO QG UV BT CI HF QY
This 100-letter ciphertext is encrypted in the double box-cipher. The plaintext is English. The two key matrices were generated with a random generator, not with a keyword.
I assume that it is possible to break this ciphertext with hill climbing or simulated annealing. One interesting question is whether this is more difficult than deciphering a Playfair cryptogram. My guess is that this is the case.
Can a reader solve this challenge?
Follow @KlausSchmeh
Further reading: Can you solve this Playfair cryptogram and set a new world record?
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/


Kommentare (18)