Wie kann man Musiknoten zum Kodieren einer geheimen Nachricht verwenden? Mit dieser Frage beschäftigen sich Menschen schon seit Jahrhunderten. Heute will ich einige Beispiele vorstellen.
English version (translated with DeepL)
Wer sich mit der versteckten Übertragung geheimer Nachrichten (Steganografie) beschäftigt, stößt früher oder später auf die Idee, Buchstaben mithilfe von Musiknoten zu kodieren. Die Idee hierzu ist schon einige Jahrhunderte alt, und natürlich gibt es in meinem Buch “Versteckte Botschaften – Die faszinierende Geschichte der Steganografie” ein Kapitel dazu.
Quelle/Source: Dpunkt Verlag
Naheliegenderweise könnte man zum Kodieren die Notennamen A, B, C, D, E, F, G nehmen (aus unerfindlichen Gründen heißt das B in Deutschland H), doch das reicht nicht aus. Immerhin lässt sich damit Buchstabenfolge B-A-C-H kodieren, was bekanntlich schon Johann Sebastian Bach gemacht hat.
Man kann auch willkürlich jeder Note einen Buchstaben zuweisen (beispielsweise kann eine halbe C-Note für das A und eine halbe D-Note für das B stehen), doch ein auf diese Weise generiertes Stück klingt reichlich seltsam. Ein musikkundiger Zensor würde sofort Verdacht schöpfen.
Im Laufe der Jahrhunderte sind zwar zahlreiche Musiknoten-Chiffren unterschiedlicher Qualität entstanden, doch eine systematische Übersicht ist mir bisher nicht bekannt. Der vorliegende Artikel soll daher eine Grundlage für eine solche Übersicht liefern. Ich werde im Folgenden ein paar Beispiele vorstellen und hoffe, dass ich durch die Anregungen meiner Leser sowie durch eigene Recherechen eine immer länger werdende Liste zusammenstellen kann.
John Wilkins
Fangen wir mit einem sehr einfachen Beipsiel an. Der Pfarrer und Kryptologe John Wilkins (1614-1672) entwickelte im 17. Jahrhundert folgenden Code:
Quelle/Source: Public Domain
Daniel Schwenter
Einen ähnlichen Code schlug ebenfalls im 17. Jahrhundert der Universalgelehrte Daniel Schwenter (1585-1636) vor:
Quelle/Source: Public Domain
Das folgende Stück enthält eine auf diese Weise kodierte Nachricht:
Quelle/Source: Public Domain
Gustavus Selenus
August II. von Braunschweig-Wolfenbüttel (bekannt auch unter dem Pseudonym Gustavus Selenus) schuf die folgende musikalischen Nachricht:
Quelle/Source: Public Domain
Auf Anregung von Blog-Leser Gerhard Strasser hat ein Orchester in den USA dieses Stück aufgenommen:
Die Nachricht ist in den gelb markierten Linien versteckt.
Maurice de Raoulx
Im Oktober 2020 habe ich über ein Musiknoten-Kryptogramm des Komponisten und Musikers Maurice de Raoulx aus dem Jahr 1854 gebloggt:
Quelle/Source: Wikimedia Commons
Blog-Leser und Jazz-Musiker Henning Wolter hat den Anfang dieses Stücks dankenswerterweise mit dem Klavier eingespielt. Es klingt nicht gerade hitverdächtig.
Meine Leser haben einiges zu den Hintergründen des Stücks herausgefunden, wie man den Kommentaren zum verlinkten Artikel entnehmen kann. Meines Wissens ist aber dennoch nicht bekannt, welche Nachricht hier versteckt ist.
William und Elizebeth Friedman
Ein weiteres Beispiel für eine Musiknoten-Chiffre ist die folgende Weihnachtskarte der Kryptologen William und Elizebeth Friedman aus dem Jahr 1933:
Quelle/Source: George C. Marshall Foundation
Unten rechts wird erklärt, wie der Code funktioniert. Zwei gleichzeitig gespielte Noten stehen für einen Buchstaben. Die Nachricht lautet: HOLIDAYS ARE HERE AGAIN WE SING OUR SONG OF CHEER AGAIN.
Mit einem Notensatz-Programm dieses Stück vertont:
Ein Meisterwerk klingt sicherlich anders. Dennoch dürfte ein solches Notenblatt nicht sofort Verdacht erregen.
Nils Kopal
Cipherbrain-Leser Nils Kopal hat letztes Jahr ebenfalls eine Musiknoten-Chiffre entwickelt. Diese ist mit der Software CrypTool anwendbar. Die Details werden im folgendem Video erklärt:
Das folgende Stück wurde mit der entsprechenden CrypTool-Funktion geschaffen:
Quelle/Source: Kopal
Wie man im Video erfährt, hat Nils einen Preis für die Lösung dieses Kryptogramms ausgesetzt. Diese wurde inzwischen jedoch gefunden.
Weitere Musiknoten-Chiffren
Es gibt natürlich noch weit mehr Musiknoten-Chiffren. Ich werde diese Liste daher sicherlich demnächst erweitern. Außerdem freue ich mich über entsprechende Hinweise.
Follow @KlausSchmeh
Further reading: Double Bottom: Ein kryptomusikalisches Gewinnspiel
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/
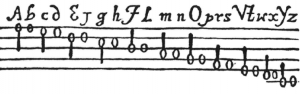
Kommentare (16)