Another ladder problem
The ladder box problem is a simple mathematical problem that is surprisingly hard to solve. And it has to do with cryptography.
In November, I blogged about the crossed ladders problem. This mathematical problem has it all: The problem looks quite unspectacular, but the solution is extremely complicated.
From a cryptologist’s point of view, the crossed ladders problem is interesting because when solving it, one encounters a second-degree multivariate system of equations. Such systems of equations form the basis of so-called multivariate crypto methods. These, in turn, are counted as post-quantum cryptography because they cannot be cracked with a quantum computer. Although there are multivariate crypto methods that can be used for encryption, only multivariate signature methods are relevant in practice.
In the crossed ladder problem, the multivariate system of equations consists of three equations, and there are three variables. This is not complex enough for a multivariate crypto method. There, one rather has to deal with 72 equations and 140 variables. Even the best computer cannot solve such a system of equations within millions of years.
There were a total of 56 reader comments after my article on crossed ladders, which doesn’t happen every day.
The review paper by Michael Schneider
Blog reader Michael Schneider has written a detailed paper on the topic of crossed ladders, which he has kindly made available to me. You can download it here. On a total of 21 pages, three solution paths are covered, including a graphical one. Really impressive!
Michael Schneider studied energy and process engineering as well as bionics and evolutionary strategy at the TU Berlin. In 1976, his first year at the university, he founded a company that wrote software for engineering and architectural firms. After graduation, he had an engineering firm for 25 years. Today he is active in the field of large-scale finance, where he works with his business friend Dr. Weisert on special capital increase (private placement) in the very high range.
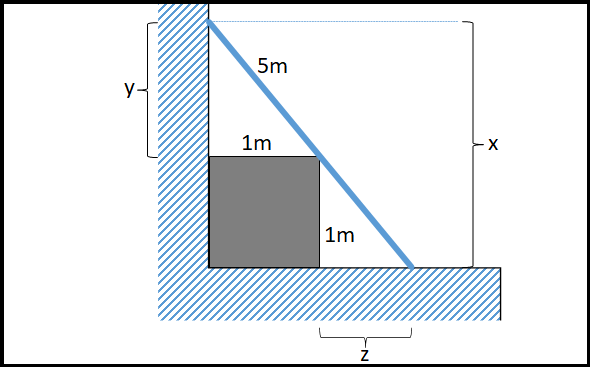
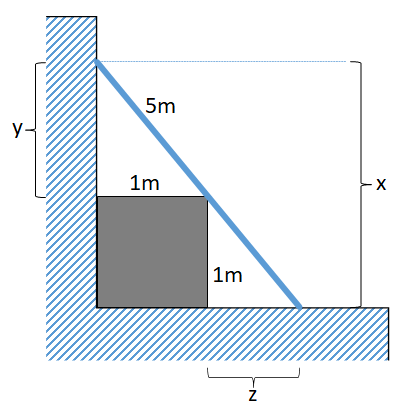
The ladder-box problem
Besides the problem of crossed ladders, there are other ladder problems. One of them is the ladder-box problem. This can be described as follows:
A cube-shaped box with an edge length of one meter stands in front of a wall. A 5 meter long ladder leans against the wall and touches the box at one edge. How high does the ladder reach?
In the drawing, x is the variable we are looking for. As you quickly realize, there are two solutions. We are only interested in the larger one.
We can now set up the following system of equations:
The first equation is derived from the Pythagorean theorem. Equation 2 can be derived from the fact that you are dealing with two similar triangles. The third equation is obvious.
You can transform the equations as follows:
Now we have a second-degree multivariate system of equations. As mentioned earlier, such systems are used in post-quantum cryptography, albeit with significantly more variables and equations.
The ladder-box problem is also surprisingly complex, considering how simple it is to describe.
On the website “Mathematical Tinkering” one can find the solution of the problem. According to it, x has the value 4.84 meters. Of course, you can also calculate the problem with other parameters.
If someone finds other solutions, I would be interested, too. I gladly accept comments.
If you want to add a comment, you need to add it to the German version here.
Follow @KlausSchmeh
Further reading:
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/


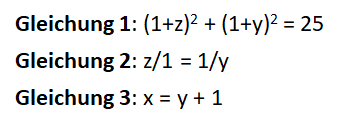
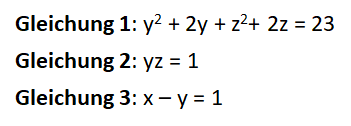

Letzte Kommentare