Blog reader Christoph Tenzer has solved the Rubik’s Cube challenge I introduced last October. His work is an amazing act of cryptanalysis.
In a Cryptologia publication from 1992, Douglas W. Mitchell proposed an interesting cipher that does not require computer support: encryption with a Rubik’s Cube.
The challenge
I described Mitchell’s cube encryption method on my blog last year in October. This method represents a transposition cipher. The colors on the cube faces are irrelevant.

Along with the cipher description, I published a challenge. I took a sentence consisting of 48 letters and encrypted it with a Rubik’s Cube. Here is the ciphertext I received:
1GDWOHOER GTNTTROI3 AET2NEV5N EIOYR6IBO WEHM4UCOD TNEIEMYET
I asked: “Can a reader break this cryptogram? If so, which codebreaking method did you use? Is Hill Climbing an option?”
The solution
Apparently, my Rubik cipher challenge was a tough one. My blog post received many comments, but for months nobody came up with a solution. But then, on March 12th, 2019, blog reader and exprienced codebreaker Christoph Tenzer, …

… an astronomer at the University of Tübingen, published the following comment:
I found the solution last weekend! It’s “Meet you at the wooden bridge in the city tomorrow evening.”
In fact, MEET YOU AT THE WOODEN BRIDGE IN THE CITY TOMORROW EVENING is the correct solution. Congratulations!
It’s by far not the first time that Christoph has broken a notable cryptogram. Especially, in 2016 he solved a ciphertext created by Alfred Janes in the 19th century. He received the Golden Alice 2016 in the “best codebreaking” section for this success.
How Christoph broke the challenge
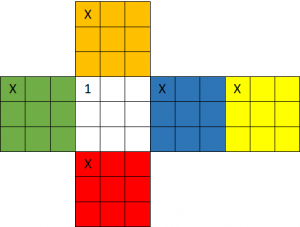
In a mail he sent me, Christoph explained how he found the solution. First of all, he read Mitchell’s paper and bought a Rubik’s Cube. He confirmed that in Mitchell’s description the orientation of the cube faces is not determined, which leads to ambiguities. To avoid these, I had defined an orientation for each face for my challenge. This is shown in the following picture:
Christoph tried several solution approaches and wrote about 10 computer programs. Most of these used Hill Climbing, but none was successful.
Christoph wrote me about his work:
I liked the idea presented by Norbert in comment #5, so I started with the approach of a hill climber that assembles the cube from scratch using the given corner-, edge- and centerpieces in different combinations. Unfortunately this didn’t work out and I still don’t know why exactly. Maybe the plaintext is too short for that with only 48 characters.
Then I thought that maybe Klaus was easy on us and used only a few moves to scramble the message. In addition, even if you use many moves to scramble the cube, there is probably a quicker path to solve it again. So I started to use an existing implementation of the moves from a library in python to shift the letters. Basically a brute-force approach. But that was way too slow to test beyond 6-7 moves deep. So I wrote my own implementation of the moves and ported everything to C++. In the end, I checked every combination of moves up to a depth of 12 for their final state. As a “check” of the state, I read off the letters and did a quadgram scoring.
A big help when breaking this code with brute-force are the numbers from 1-6. There must be exactly one on each side for a solution to be valid. So I could skip the quadgram scoring almost all of the time. With some additional ideas, I didn’t have to check every possible move as some just undo the previous moves or combinations like MC90,MC90,MC90 can be reduced to just MC270 in Klaus’ notation. Still, the program took about two weeks on my desktop PC to find a readable (but not yet fully unscrambled) solution from which one could conclude on the plaintext.
Here’s a translation of some more information Christoph provided me:
I think that Brute Force renders quite acceptable solution times. I was able to test about 4,500,000 “keys”, i.e. move combinations, per second, and evaluate those where the 6 numbers landed on different sides using quadgram scoring. Since there are always many ways to get a certain twist, evaluation of many ways can be skipped. My impression is: even if you use a key consisting of 20 moves, there is probably a much shorter way to the solution the Brute Force program will find in an acceptable time.
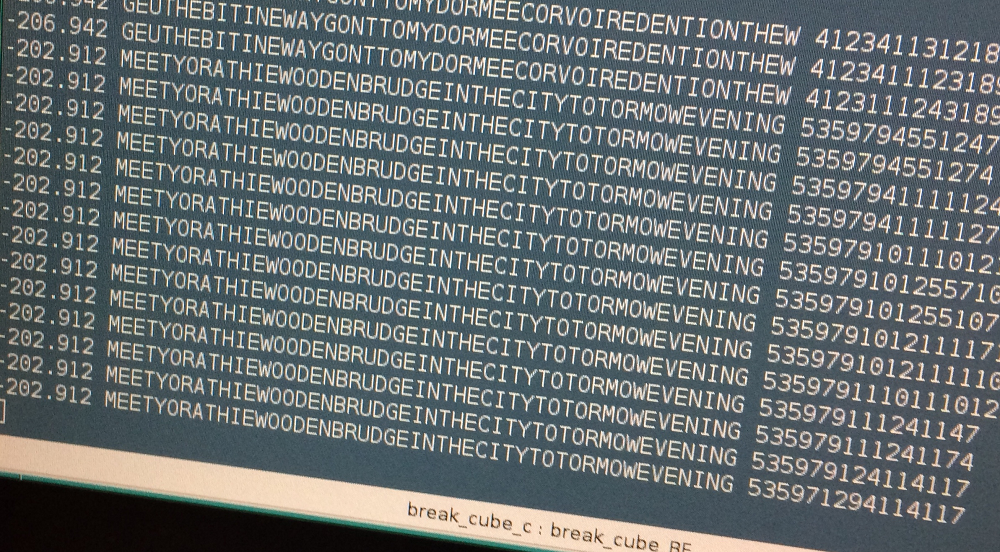
In the screenshot you can see a state where the text was recognizable for the first time. The number on the left is the quadgram score, followed by the plaintext candidate and the move combination. Each number in it (5, 3, 5, …) stands for a certain twist like MC90, MC180, etc.
It goes without saying that I am absolutely impressed by Christoph’s codebreaking work. As it seems, he has was the first to deliver a proof that Mitchell’s cipher algorithm from 1992 is not secure. This is absolutely amazing. Congratultions and thanks for this outstanding contribution to my blog!
Follow @KlausSchmeh
Further reading: Blog reader Norbert Biermann solves famous 16th century crypto mystery
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/



Kommentare (5)