Das Leiter-Kiste-Problem ist eine einfache mathematische Fragestellung, die erstaunlich schwer zu lösen ist. Und sie hat mit Kryptografie zu tun.
English version (translated with DeepL)
Im November habe ich über das Problem der gekreuzten Leitern gebloggt. Dieses mathematische Problem hat es in sich: Die Fragestellung sieht recht unspektakulär aus, doch die Lösung ist äußerst kompliziert.
Aus Sicht eines Kryptologen ist das Problem der gekreuzten Leitern interessant, weil man beim Lösen auf ein multivariates Gleichungssystem zweiten Grades stößt. Solche Gleichungssysteme bilden die Grundlage von so genannten multivariaten Krypto-Verfahren. Diese wiederum werden zur Post-Quanten-Kryptografie gezählt, da sie nicht mit einem Quanten-Computer geknackt werden können. Es gibt zwar multivariate Krypto-Verfahren, die sich zum Verschlüsseln nutzen lassen, doch praxisrelevant sind nur multivariate Signaturverfahren.
Beim Problem der gekreuzten Leitern besteht das multivariate Gleichungssystem aus drei Gleichungen, und es gibt drei Variablen. Für ein multivariates Krypto-Verfahren ist das nicht komplex genug. Dort hat man es eher mit 72 Gleichungen und 140 Variablen zu tun. Ein solches Gleichungssystem kann selbst der beste Computer innerhalb von Jahrmillionen nicht lösen.
Insgesamt gab es nach meinem Artikel über die gekreuzten Leitern 56 Leserkommentare, was nicht alle Tage vorkommt.
Die Übersichtsarbeit von Michael Schneider
Blog-Leser Michael Schneider hat zum Thema der gekreuzten Leitern eine ausführliche Abhandlung verfasst, die er mir dankenswerterweise zur Verfügung gestellt hat. Hier kann man sie herunterladen. Auf insgesamt 21 Seiten werden drei Lösungswege behandelt, darunter ein grafischer. Wirklich beeindruckend!
Michael Schneider hat Energie und Verfahrenstechnik sowie Bionik und Evolutionsstrategie an der TU Berlin studiert. 1976, in seinem ersten Jahr an der Universität, gründete er eine Firma, die Software für Ingenieur- und Architekturbüros schrieb. Nach Abschluss des Studiums hatte er 25 Jahre lang ein Ingenieurbüro. Heute ist er im Bereich der Großfinanzen aktiv, wo er sich mit seinem Geschäftsfreund Dr. Weisert um Spezial-Kapitalvermehrung (Privat Placement) im sehr hohen Bereich kümmert.
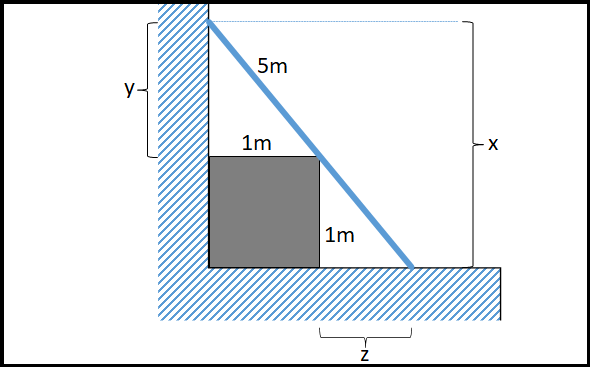
Das Leiter-Kiste-Problem
Außer dem Problem der gekreuzten Leitern gibt es noch weitere Leiterprobleme. Eines davon ist das Leiter-Kiste-Problem. Dieses kann man wie folgt beschreiben:
Eine würfelförmige Kiste mit einer Kantenlänge von einem Meter steht vor einer Wand. Eine 5 Meter lange Leiter lehnt an der Wand und berührt dabei die Kiste an einer Kante. Wie hoch reicht die Leiter?
In der Zeichnung ist x die gesuchte Variable. Wie man sich schnell klar macht, gibt es zwei Lösungen. Uns soll nur die größere interessieren.
Man kann nun folgendes Gleichungssystem aufstellen:
Die erste Gleichung ergibt sich aus dem Satz des Pythagoras. Gleichung 2 kann man aus der Tatsache herleiten, dass man es mit zwei ähnlichen Dreiecken zu tun hat. Die dritte Gleichung ist offensichtlich.
Man kann die Gleichungen wie folgt umformen:
Nun haben wir ein multivariates Gleichungssystem zweiten Grades. Wie bereits erwähnt werden solche Systeme in der Post-Quanten-Kryptografie verwendet, wenn auch mit deutlich mehr Variablen und Gleichungen.
Auch das Leiter-Kiste-Problem ist erstaunlich komplex, wenn man bedenkt, wie einfach es zu beschreiben ist.
Auf der Webseite “Mathematische Basteleien” findet man die Lösung des Problems. Demnach hat x den Wert 4,84 Meter. Natürlich kann man die Aufgabe auch mit anderen Parametern durchrechnen.
Falls jemand andere Lösungswege findet, würde mich das natürlich auch interessieren. Kommentare nehme ich gerne entgegen.
Follow @KlausSchmeh
Further reading:
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/


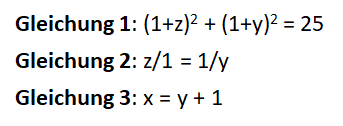
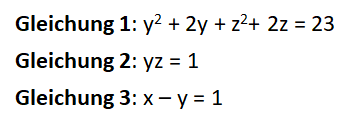

Kommentare (5)