Today I’m presenting a 24 letter message that has been encrypted with a Playfair cipher. Such a short Playfair cryptogram has never been solved before.
In December, I reported on Konstantin Hamidullin’s solution of a Playfair challenge I had published four weeks earlier. With only 26 letters, this cryptogram is the shortest Playfair message that has ever been broken.
Playfair cipher records
Konstantin’s deciphering success was already the fifth Playfair world record set by my blog readers. Here are the four previous ones:
- Magnus Ekhall broke a 28-letter Playfair message.
- Magnus Ekhall broke a 30-letter Playfair message.
- Nils Kopal broke a 40-letter Playfair message.
- George Lasry broke a 50-letter Playfair message.
In all of these cases, a Playfair cipher with a random matrix (i.e., not based on a keyword) was used. US cryptanalyst Alf Monge broke a 30 letter Playfair back in the 1930s, but this one was keyword-based, which made things easier.
According to George Lasry, the unicity distance for a Playfair cipher applied on an English text is 22. This means that a ciphertext of 22 letters or shorter does not have an unambiguous solution. If the ciphertext is longer, a unique solution exists and can be found – at least in theory.
Hill climbing appears to be a good method for breaking a Playfair encryption. George, Nils, and Magnus used this technique for their record-breaking cryptanalysis successes. Their work has considerably improved the hill climbing methods applied in codebreaking. To my big surprise, Konstantin didn’t use hill climbing when he set the current record. Instead, he conducted an exhaustive search with several optimizations. Each solution candidate was checked with a fitness function.
—————————————–

I’m excited to announce I’ll be speaking at RSAConference 2020 on UNDERSTANDING AND EXPLAINING POST-QUANTUM CRYPTO WITH CARTOONS.
—————————————–
How the Playfair works
I’m sure that meanwhile most readers of this blog know how the Playfair cipher works. For those who don’t, this section gives an introduction.
The Playfair cipher substitutes letter pairs. So, the cleartext needs to be written as a sequence of letter pairs (the following cleartext is a Shakespeare quote taken from Robert Thouless’ life-after-death experiment):
BA LM OF HU RT MI ND SG RE AT NA TU RE SS EC ON DC OU RS EC HI EF NO UR IS HE RI NL IF ES FE AS T
The Playfair cipher requires that no letter pair consist of two equal letters. Therefore, we add an X between the two Ss:
BA LM OF HU RT MI ND SG RE AT NA TU RE SX SE CO ND CO UR SE CH IE FN OU RI SH ER IN LI FE SF EA ST
If the number of letters in the cleartext is odd, another X needs to be added at the last position, but this is not the case here. Next, we set up a 5×5 matrix containing the letters of the alphabet in a random order (we identify the J with the I, in order to get a 25 letter alphabet):
S U R P I E A B C D F G H K L M N O Q T V W X Y Z
As you might have noticed, the letter order in the matrix has been derived with the keyword SURPRISE. It would be more secure to use a completely random order of the letters.
Now, we replace the cleartext letter pairs (BA, LM, OF, HU, …) according to the three Playfair rules. Here are the rules in a diagram:
Here are the same rules in text form (I refer to the letter pair to be replaced as XY):
- If X and Y are not in the same column and not in the same row (this is the most frequent case), form a rectangle and replace the two letters by the other two corner letters (the upper cleartext letter is replaced by the other upper letter in the rectangle, the lower cleartext letter by the lower one). For instance, LM becomes FT.
- If the two letters stand in the same row, each one is replaced by its right neighbor. Here, BA becomes CB.
- If the two letters stand in the same column, each one is replaced by its lower neighbor. In our example, AN becomes GW.
When we apply the Playfair rules on our cleartext with our 5×5 matrix, we get the following ciphertext:
CB FT MH GR IO TS TA UF SB DN WG NI SB RV EF BQ TA BQ RP EF BK SD GM NR PS RF BS UT TD MF EM AB IM
A new challenge
After my 26 letter ciphertext had been solved by Konstantin Hamidullin, I created a new challenge based on an even shorter message. This time, I chose a ciphertext consisting of 24 letters. As usual, I used the Playfair function of the software CrypTool for encryption.
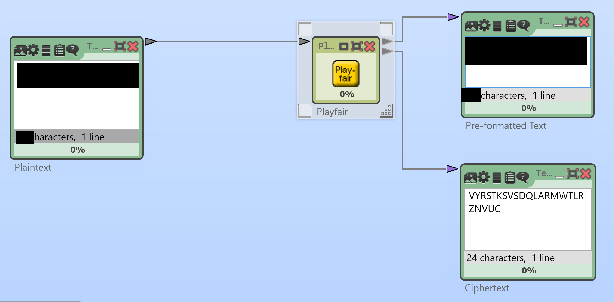
Here’s the ciphertext I received:
VYRSTKSVSDQLARMWTLRZNVUC
Can you decipher this message? If so, you will set a new world record.
Edited to add: The ciphertext I presented first (BZR…) was wrong. It contained a J, which is not possible in the standard Playfair cipher.
Follow @KlausSchmeh
Further reading:
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/
[jetpack_subscription_form title=”Subscribe to Bl




Kommentare (10)