StartseiteCipherbrain

Revisited: What does the pseudonym “46, 9, 4-57, 3, 5” stand for?

Von / 15. Januar 2018 / 30 Kommentare
Mehr

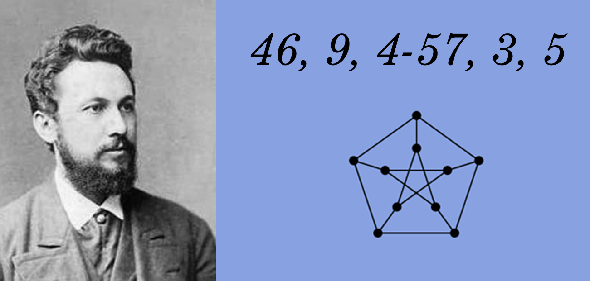
This is the shortest cryptogram I have ever introduced on this blog: 46, 9, 4-57, 3, 5. Can a reader decipher it?

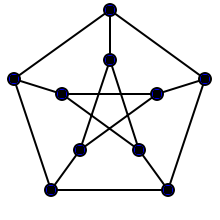
Julius Petersen (1839-1910) was a Danish mathematician, whose work led to the birth of graph theory. He ist best known for Petersen’s theorem (“every cubic, bridgeless graph contains a perfect matching”), and the Petersen-Morley theorem.

Petersen

Moreover, he created the Petersen graph, which looks like this:

Petersen-Graph

Petersen’s cipher signature

Julius Petersen also had an interest in encryption. In 1875 he published a cryptography pamphlet titled Système cryptographique written in French (I haven’t found this pamphlet online, does a reader know where it is available?).

Petersen-Pamphlet

A principle emphasized in this pamphlet states that the security of a cryptosystem must not depend on keeping the crypto-algorithm secret. Instead, the security should depend only on keeping the key secret. This concept is today known as Kerckhoffs’ principle, named for Auguste Kerckhoffs (1835-1903), who stated it 18 years after Petersen, in 1893.

Petersen also wrote (or co-wrote) a series of eight fortnightly articles on cryptography for a weekly magazine named Nær og Fjern (if a reader knows where these articles are available, I would be interested, too). These articles were published under the following pseudonym:

46, 9, 4-57, 3, 5

As it is not clear whether Petersen was the sole author of this article series, it is not known if this pseudonym refers to him alone or to a group of persons he belonged to.

The meaning of 46, 9, 4-57, 3, 5 is unknown. It is the shortest cryptogram I have ever written about on this blog (except for the infamous Riverbanks Ripper cryptogram, of course).

 

Many comments, no solutions

My main source for the Petersen signature (except for a Cryptologia article from 2006)  is a blog post written by Nick Pelling in 2010.  It received 20 comments. Four years later, I wrote my first blog article about this mystery (in German), which was commented by my readers, too. Some of the comments were quite interesting:

  • René Zandbergen remarked that 46, 9, 4-57, 3, 5 might stand for two dates (perhaps 1846-09-04 and 1857-03-05). Are these the birth  and death dates of a person who died in the age of eleven?
  • Ernest Lillie wrote: It looks like a book code. I’d speculate that it goes something like: Page 46 — Line 9 — Word 4 = Julius; Page 57 — Line 3 — Word 5 = Petersen. It would make sense if the book used as the key had an alphabetical listing of names and ran to about 90 pages. Worldcat says that “Système cryptographique” has 15 pages so no joy there.

However, none of these comments led to a solution. So, four years after my first try, I decided to introduce this cipher mystery on Klausis Krypto Kolumne again. Are there any new ideas about this short cryptogram? If so, please let me know.


Further reading: The silk dress cryptogram: New evidence, but solution still not found

Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/

Subscribe to Blog via Email

Enter your email address to subscribe to this blog and receive notifications of new posts by email.

Stichworte:
Mehr

Kommentare (30)

  2. #2 Peter
    16. Januar 2018

    Das Buch kann wahrscheinlich in der Bibliothek von Harvard gescannt werden…. hätte man denn einen Zuganscode. In:

    https://hollis.harvard.edu/primo_library/libweb/action/search.do?vid=HVD

    Autor eingeben, das richtige Buch anwählen. Dann gibt es einen Link “Scan and deliver”.

  3. #3 Patric Hausammann
    Basel (Schweiz)
    16. Januar 2018

    Ich hätte da zwei Vorschläge. Wie wäre es mit “Crypthos” > “Krypthos” als Lösung?^^ Dabei ist zu beachten, dass sich aus “Kryptos” mit ausreichendem Hintergrundwissen “Petersen” (>Peterson ^^) herleiten lässt!^^

    ✨
    ‍ © by Patric Hausammann  aka 10 + 10 < also a kind of riddle

  4. #4 Patric Hausammann
    Basel
    16. Januar 2018

    Nachtrag, resp Korrektur: Mit Krypt(h)os meinte ich die alte Schreibweise von “Kryptos”(De.) “Cryptos”(Eng.). So wie, dass das “Alphabet” früher in der Form “Alphabeth” geschrieben wurde.^^

    ‍ © by Patric Hausammann

  5. #5 Patric Hausammann
    Basel (Schweiz)
    16. Januar 2018

    Nachtrag 2:
    46, 9, 4-57, 3, 5

    4,6,9,4 – 5, 7, 3, 5
    d,f,i,d – E, G, C, E >> dargestellt als nummerierte “Stellenaufzählung” > (1 >mirrored “e”},4{p>>t} – 5{E/S}^^,8{S},7,6) >> Piet(e/s)son Pietersen Peterson.

    © by Patric Hausammann

  6. #6 Patric Hausammann
    Basel (Schweiz)
    16. Januar 2018

    Warum fehlt da die Hälte meiner Angabe?
    Deshalb nochmals in ergänzter Form:

    d,f,i,d – E, G, C, E >> ( dargestellt als nummerierte “Stellenaufzählung” nach voran gegangener eigener Aufstellung ) > 1 > P, 3 > i, 2 > f-1 Buchstabe im Alphabet = e, 4 > t, – > Platzhalter =Hagall*, 5 >E/S, 8 > E/S, 7 > O/E, 6 > N

    >> Piet(e/s)son / Pietersen / Peterson > Fils de Pierre (Fr.) > Filius Petri (Lat.) {das Wort besteht aus 10 Stellen und ist “getrennt in zwei gleich grosse Teile ^^}

    © by Patric Hausammann

  7. #7 Thomas
    16. Januar 2018

    In his book (written in French) Petersen not only mentioned the cipher security principle before Kerckhoff, but also described a fractionated cipher based on letter coordinates similar to Bifid before Delastelle did it (Honni soit qui mal y pense!)

  8. #8 Patric Hausammann
    Basel (Schweiz)
    16. Januar 2018

    Ich hab nochmals einen kleinen Nachtrag betreffend der 10 erwähnten Stellen, damit es nicht zu Missverständnissen oder komischen Fragen kommt. Denn eigentlich sind es hier ja, je nach Sichtweise (> 46, 9, 4-57, 3, 5 ) verschiedene Anzahlen an Zeichen.. Die meisten werden im Zahlenrätsel eine Anzahl von > 6 (ohne “-” Minus/Bindestrich) bis 9 verschiedene Zeichen oder Platzhalter erkennen(dies sind die offensichtlichsten Varianten).^^ Die Anmerkung in der Klammer sollten sich eigentlich auf den Begriff “Peters Soehne” (Deutsch plural >12 Zeichen) beziehen, ich hatte aber auch zurselben Zeit die englischen Varianten > “Son of Peter” > “Peter’s son” im Kopf, um dem Leser zu helfen die Teilungsverhältnisse zu visualisieren (Zahlenrätsel hat auf beiden Seiten die gleicher Anzahl mit Buchstaben, abgesehen vom “- “als Trennzeichen). Ich wollte damit eigentlich auf einen Wechsel vom Ungleichgewicht zum Gleichgewicht hinweisen.^^ Möglicherweise, ist es auch genau das, was Herr Petersen (8 Zeichen) mit diesem Rätsel darstellen wollte. 😉 Da ist jedoch meines Erachtens noch mehr dahinter. 😉

    © by Patric Hausammann

  9. #9 Patric Hausammann
    Basel (Schweiz)
    16. Januar 2018

    Very good Thomas, thank you for your comment!

    Greetings from Switzerland!

  10. #10 Thomas Ernst
    Latrobe
    17. Januar 2018

    Sometimes it helps to see things in their original context. Petersen appears to have published at least eight articles on cryptography in the Journal “Nær og Fjern”, which can be found at: https://books.google.com/books/about/N%C3%A6r_og_Fjern.html?id=sF9NAZgWBIQC. Each article is headed in the same manner: “LØnskrift eller Kryptografi. | Af 46, 9, 4–57, 3, 5. | [follows wavy line] | [follows instalment no. in Roman numerals].” All the eight signatures are identical, there is no “slip” or variation. I was hoping the articles were signed at the end, in a more jounalistic fashion, where one could expect sth. like “J. P.”, or “Ju Pe”. Unfortunately, most of the contributors to “Nær og Fjern” appear to have signed their full first and second name, with occasional exceptions, e. g. the music critic “Ed. Hanslick”. For that reason I find the theory that the eight numerals, via some byways, correspond to eight letters, i. e. “Petersen”, improbable. However, Marc’s purely mathematical approach – last entry in Nick Pellings blog, and in greater detail in Klaus’ first presentation of this cipher – is very appealing, albeit not the final word. Things like checksum “46” = “10” = “J” and that you can achieve the same result – as Marc did – by “46 – (9×4)”, not to mention the identical outposts “4” in the first, “5” in the second group, make me think of some sort of mathematical SATOR-scheme, in which the two sets à 4 numerals have to be “equated” in several ways. The long hyphen between both groups link directly from 4 to 5, “4–5”. It may be worth checking the typographical use of hyphens elsewhere in “Nær og Fjern” to see whether this type and placement of hyphen is unusual on purpose, or just printer convention. – Perhaps one may find inspiration in Petersen’s articles VII and VIII, in which he describes Orloff’s numerical ciphers. They contain numerical homophones. But I think it’s more a matter of equations, and the repeated use of numerals therein.

  11. #11 Klaus Schmeh
    18. Januar 2018

    William Higinbotham via Facebook:
    Maybe someone could go to these places and copy the book? (I haven’t found this pamphlet online, does a reader know where it is available?) https://www.worldcat.org/search?q=Syst%C3%A8me+cryptographique+julius+&qt=results_page#%2528×0%253Abook%2Bx4%253Aprintbook%2529format

  12. #12 Thomas
    18. Januar 2018

    The number cryptogram has nothing to do with Petersen`s own fractiionating cipher which is presented in this article: https://docslide.net/download/link/julius-petersendanish-mathematician-and-cryptologist

  13. #13 Patric Hausammann
    Basel (Schweiz)
    18. Januar 2018

    Dear Thomas,
    Thank you very much for sharing this article! It seemed first, that there was something wrong with the file. But I managed to open it. If someone else has the same trouble. You only have to delete the apostrophe ( ‘ ) at the beginning and at the end of the files name.

  14. #14 Thomas Ernst
    Pittsburgh
    18. Januar 2018

    Three things:
    • Regarding the two use of the long hyphen in “Nær og Fjern”. First, it is used to set off two sections of text, for emphasis or additional comment; random example “NoF”, Nr. 118, p. 8: “[…] men ogsaa – infandum dictu! – Theologerne ved […]”. In that case, there are always spaces before and after the hyphen. Secondly, it is used, without space, when connecting two names; for example “NoF” Nr. 118, p. 9 (same article): “[…] er Konstellationen Tegnér–Ling ret interessant […] med Konstellationen Oehlenschläger–Grundtvig.” This makes the theory of double authorship more plausible. Which does not mean that “46, 9, 4” has to be one, “57, 3, 5” the other contributor – they could have intertwined their initials.
    • In Nick Pelling’s post, Bjarne Toft is quoted as having stated “we know from other sources that [Petersen] was the author (or one of the authors)“. So I wrote to Professor Toft and asked him, whether he could elucidate on these other sources. Not that I have any doubts that Petersen indeed (co-)wrote those articles, but because of the “how” these other sources knew – which may throw some light on how this cipher was concocted. Especially if a second author was involved, he/she may have left a written memoir of “how” they signed these articles. If it’s two people, I can’t really think of anything else than the numbers standing for initials. The Danish alphabet has 29 letters (more if you count additional diacritics – see the wisdom of Wiki on that matter), the “c” however, though considererd a “foreigner”, was usually included in the count. So checksum “46” = 10th letter = “J” might just hold water …
    • I have asked Harvard whether I could obtain a digital copy of Petersen’s “Système”. Their reply, as is customary, will depend on the condition of the book.
    Will share what I find out when I find out.

  15. #15 Thomas Ernst
    Latrobe
    19. Januar 2018

    No answers to my requests yet. Just a little more checksum/subtraction play on the first four numerals: 46 = 4 + 6 = 10 = “J”. 46 – 9 – 4 = 33 = 3 + 3 = 6. Checksums 10 + 6 = 16 = “P”. Within the equation, the “46” and “57” would count at face-value, and cryptologically as checksums, with the commata as minus-signs. With that sort of math, the second set of letters would be “L” and “Y” (assuming “Y” is the 25th letter of the alphabet Petersen used). Thus perhaps no co-author, but a placename: “Julius Petersen–Lundby”. Today, so Wiki informs, Lundby is a town with 825 inhabitants. Wonder how they were counted. However, Lundby is not far (south-east) from Petersen’s birth place SorØ. I do not know whether Lundby has a role in Petersen’s biography.

  16. #16 Thomas Ernst
    Latrobe
    20. Januar 2018

    Progress report:
    a) please forget my cabbalistic computations in previous posts. If you are right 90% of the time, who cares about the remaining 5%.
    b) Bjarne Toft replied within one day, very kindly so, very informatively so. To those who have access to “Cryptologia”, vol. 30, 2006, the articles on Petersen (authored by Augusto Buonafalce, Niels Faurholt, and Bjarne Toft), as well as the article on Alexis KØhl (authored by Niels Faurholt), will be familiar. To me, they were not. To be brief: external evidence that Petersen authored the eight articles in “Nær og Fjern”, May to August 1875, comes from a remark by Alexis KØhl, in his privately printed pamphlet from 1916, “Nogle Resultater paa det tekniske Omraade” (“Some achievements in the field of technology”). There he states that Petersen’s articles in “NoF” inspired his own – KØhl’s – lifelong fascination with cryptology. Whether the two ever met, is not documented; however, to paraphrase the Petersen-article, Copenhagen, at the time, was a small town. In addition, KØhl published similar cryptological concepts to those of Petersen, although he appears to have been intrigued more by cryptological machines (such as a cryptological typewriter – link at: https://oztypewriter.blogspot.dk/2014/02/khls-kryptograf-writing-ball.html).
    The authors of the Petersen-article gave, according to their own words, a simplified (!) version of Petersen’s “Système”, apparently of their own making, since it is in English. – However, one remarkable detail emerged from this summary: by way of metamorphosis of fractionated digraphs, Petersen concluded with “Send ciphertext by telegraph in five letter groups. (Ciphertext has same length as original plaintext).” Follows the authors’ illustration “NTBMO GTHBT JGZZR […]”.
    For me, the five-letter-groups are the main thing here. Because in “NoF”, we have two four-letter groups, “46, 9, 4”, and “57, 3, 5”. If we diminish the 5-letter-groups to 4-letter groups, the hyphen would not be a semantic separator, but rather a cryptological one: “PETE RSEN”. Or perhaps in abbreviated form: P[eter]J[ulius]CH[ristian]_PET[erso]N. Whichever you prefer, his name it is. – Remains the signifiant-signifié problem: while in his “Système”, Petersen ended up with letters derived from tomographically morphed digraphs, in “NoF”, you have numerals. My only thought on this: perhaps he suggested a reverse of his “system”, where you start out with morphing alphabetical pairs, and end up with numerals. – It appears that in his eight articles, Petersen gave “tasks” to his readers, like Bellaso did some 300 years before him, or John Holt Schooling 20 years after him. Apparently, readers of “NoF” didn’t just have molten lava cake between their ears, since, supposedly, they figured out some of them. Do not know, however, whether all of them. This requires a little foresting through “NoF”.
    All of which really, really necessitates a close reading of the original “Système”. By 2006, Buonafalce/Faurholt/Toft had located only 6 copies: 1) Royal Library in Copenhagen, 2) State Library at Aarhus, 3) Schleswig-Holsteinische Landesbibliothek in Kiel, 4) Fisher Collection in Toronto, 5) Harvard University, 6) Vienna Haus- Hof und Staatsarchiv. If you have the good luck to live in Europe, i. e. the civilized world, what better excuse for a nice séjour in beautiful Kiel at the Baltic, or in beautiful Vienna at the not-so-blue Danube? – Today, I put in my own begging for a digitalisation of the Harvard copy through my “institution’s” inter-library loan (after recent Ferdinand-success, my chair said: anything you want … YES!!!). – However, you, the reader, may be faster in obtaining a copy from Kiel or Wien.
    Will gladly share the two “Cryptologia” articles, but am not sure whether I can do so in a public forum.
    Once I receive digitalisiation of original “Système (and Harvard hasn’t agreed, yet – over here, they think 100 years is a long time, while 100 miles are nothing -, will gladly share it.
    Having read the description of Petersen’s system, I am tempted to agree with him: you grasp the system. But without the key, you can’t solve the cipher, unless by circumstantial means.
    More anon.

  17. #17 Thomas
    20. Januar 2018

    Buonafalce’s et al. article is already linked in my post #13. Having read this article I doubt that the number cryptogram is based on Petersen’s fractionating cipher. Nevertheless I ordered a copy of the “Systeme” from the SHLB in Kiel, but up to now I’ve got no answer.

  18. #18 Klaus Schmeh
    20. Januar 2018

    William Higinbotham via Facebook:
    So I contacted Harvard University that has a copy. This is their reply! Dear Mr. Higinbotham,

    I have bad news and good news. The bad news is that the book you are seeking is not available at this time. The good news is that it is not available because it is on its way to be scanned by the Google Books project. This means that in the foreseeable future, our copy will be freely available in digital format through Google.

    We thank you for your request and for your patience as we both wait for the digitization to occur.

    Best,

    – Tom

    Thomas A. Lingner
    Customer Service Manager
    Imaging Services

  19. #19 Klaus Schmeh
    20. Januar 2018

    @Thomas Ernst: Thank you very much for doing this research!
    For those who don’t know: Thomas Ernst solved (most likely) a very similar mystery (about a 19th century crypto author who called himself „; + 1 Λ + o“) in 2016. A really great story and a highlight in the history of this blog.
    https://scienceblogs.de/klausis-krypto-kolumne/2016/01/14/top-25-krypto-raetsel-wahrscheinlich-geloest-teil-2/

  20. #20 Thomas Ernst
    Pittsburgh
    20. Januar 2018

    If I remember correctly, my “solution” of „; + 1 Λ + o“ belonged to my 5% … – Thomas’ link in # 12 didn’t work for me – I couldn’t even get past the “confirm” button. – If “Google Books” got their grubby hands on Harvard’s copy, the digitization may take place, but there is a good chance you will only get the infamous brown-cover book-corpse on your screen, i. e. a digitization which you can’t open. – Petersen’s 8 articles appeared May-August 1875, his “Système” in November of the same year. Thus there is a good chance that he had the concept of his own tomographic cipher, or a precursor thereof, already in mind while writing the articles. Given that the hyphen separates two equal amounts of signs, whether you count 4–4 or 6–6 including the commata, and that Petersen intended the text enciphered by way of his “système” to be divided into equal amounts of letters makes me believe that the hyphen in his signature is purely steganographic, if you will, implying two words, where there actually is only one. As already mentioned, I think his two articles – 6 and 7, if I remember – on the Orloff cipher, dealing with numerical pairs – may be of some help. Along with a good Danish dictionary and grammar … The link to “Nær og Fjern” is in my # 10.

  21. #21 Thomas Ernst
    Latrobe
    21. Januar 2018

    I think an answer to our cipher might be found in Petersen’s last article – the second Orloff-installment – which he himself called “sidste”, “last”, in “NoF” 164, pp. 6-9. At that point, Petersen apparently was done with his articles on cryptography.

  22. #22 Thomas
    21. Januar 2018

    @Thomas Ernst
    But due to Orloff’s cipher disk both systems use only the numbers from 10 to 54. If the cryptogram were based on one of these systems, an additional mathematical step would be needed. Unfortunately Google translate cannot read Fraktur.

  23. #23 Gerry and Andrea
    22. Januar 2018

    Maybe it is his his encrypted nickname „Sorte Peter“ (Black Peter), which is mentioned in his biography at https://ac.els-cdn.com/0012365X9290636T/1-s2.0-0012365X9290636T-main.pdf?_tid=dc947c40-fef8-11e7-8a39-00000aab0f26&acdnat=1516573226_7168c40c50adb2de8897bfff2459aff7

  24. #24 Thomas Ernst
    Latrobe
    22. Januar 2018

    @ Thomas: I guess the only way around Google’s inability to read Fraktur is to simply copy passages into modern typeface, and then get a decent translation. Often, Danish is close enough to German to get a partial understanding. Which, of course, is a dangerous thing. – I keep going back to some simple similarities: both Petersen (in his Système”) and Orloff finished their encipherments by grouping them in fives – single letters with Petersen, double numerals with Orloff (if I understand “NoF” 162, p. 5, correctly). True, Orloff’s cipher disk only went from 10 to 54. However, that doesen’t mean that Petersen couldn’t have finessed something. As a matter of fact, I can’t help but think that Petersen’s signature doesn’t exceed the material he presents in his eight articles but by perhaps only one step. Twenty years later, John Holt Schooling did something similar with his keyed “nihilist”-cipher (which Elgar was so proud of having solved). However, Schooling meant his final task just as that – a final exercise. Petersen’s signature is not a task per se, but a by-product of his articles on cryptography. It probably is not even that difficult to solve – IF one has read all of his eight articles. I no longer think we’ll find an answer in his “Système”. No, the solution to the enciphered signature is bound up with the eight articles. Which brings me to the possibility (!) of reading it as “46 94 57 35”, the hyphen still being a steganographic separator between equal amounts of signs. Muliplication would bring us back into Orloff’s range: “24 36 35 15”. Which may stand for: “Af JP”. – Speculation, nothing but, because a full grasp both of Orloff’s system as well as Petersen’s description and critique thereof eludes me because of the language barrier.

  25. #25 Thomas Ernst
    Latrobe
    22. Januar 2018

    Need to emend my previous comment: within the confines of only four signifiers, the preposition “Af” is needless. In addition, in “NoF” no-one ever signed that way. Thus, if my above hypothesis should turn out to be true, the four “signifiants” should rather be “JuPe”. “JChP” is unlikely, since it leaves too much doubt about the “P”. In other words: a four-letter-only signature would need to be sufficiently succinct.

  26. #26 Thomas Ernst
    Latrobe
    22. Januar 2018

    PPS: if we take the commata not as steganographic, but as mathematical signs, the sequence of four signifiers could change into “46 36 57 15”, or “10, 36, 12, 15”. Food for thought.

  27. #27 Patric Hausammann
    Basel
    8. Februar 2018

    Maybe it was Sir William Rowan Hamilton (1805-1865), who has inspired Julius Peterson to his cipher. Maybe they knew each other personally (both were mathematicians). I mention “Hamilton”, because of his work of the “Icosian game”(>dodecaheder), which reminds me very much to Petersen’s cipher signature. 😉
    It seems to me, that Petersen adapted his idea from Hamilton, but changed the “appearence” of the inner pentagon to a pentagram. Maybe the number riddle means “Hamilton & Petersen” or something similar in its meaning. 😉

    © by Patric Hausammann

  28. #28 Patric Hausammann
    Basel
    8. Februar 2018

    I’ve got a further idea, about Hamilton(-1) and Petersen (1). Could it be that they were members of the same “club”. I know that sounds a bit funny but think about “Man – Son” > “Manson”. “Manson” in general means something like “human” to me. I think this term is very interesting! You can make a wordplay with it, and it gives us “nos nam” > “our name”. 😉 It is like the term “Huns” > “Hunnen” (Ger.), which meant “human too, but humans are same, but different. It is a bit like Ying and Yang, for example the French people used the term “Hun” as a place holder for the “bad” Germans during WWII. It is like ” For the good, the good is good and for the bad, bad is good or vica versa” ;). Think about: +*+=+ and -*-=+ (math rules 😉 )
    Or could there be a hidden prediction? 😉 Hm, “Neumann” (Newman) … {NOMEN EST OMEN}

    © by Patric B. Hausammann פטריק הטוב ביתהאדם 😉

  29. #29 Patric Hausammann
    8. Februar 2018

    Supplementary information about the sentence with the “vica versa ” example. I actually wanted to show of the mathematical relation of +*+=+ & -*-=+ and +*-=- -*+=- . Sorry, about my vagueness!

    © by Patric Hausammann

  30. #30 Patric Hausammann
    Basel
    8. Februar 2018

    I hope you could follow my suggestions from above. I think it has to do with the term “Axiom” (> one axis (axle) 😉 / one center(re)/ arbor (link to >arbre >vvood> tree>ship wipe(s) > float(s) 😉 / shaft / pivot / roller /cylinder / cyl / / topper / top hat / silk hat / valuation / estimation / decision / judgment / sentence / verdict / decree / appreciation / AE > AXIOM EONES(beginning and ending {“to be”} or also a link to “LIBRA”, “scale”, “chart” or “balance”) > ET 😉 ). This seems like a description of the primary rules, to be able to choose between something or someone (meaning of the word “Torah” /”Thora” /”Tora” is “instruction” resp. “teaching”! > 😉 ). Think about the “Torah” or the Old Testament in the Holy Bible. The ones who read it may agree, if they understand it the “right” way. 😉
    I guess, this is the “root” of logical thinking! But to realize this, it requires a little wisdom (> “Weisheit” German) 😉

    © by Patric Hausammann بيت الشع جيدة باتريك 😉